Dynamic programming of PHP algorithm learning (2)

I briefly introduced the concept and solution steps of dynamic programming before, but during the study, I felt that the application scope of dynamic programming is too flexible. Here I will pick some common questions and practice more.

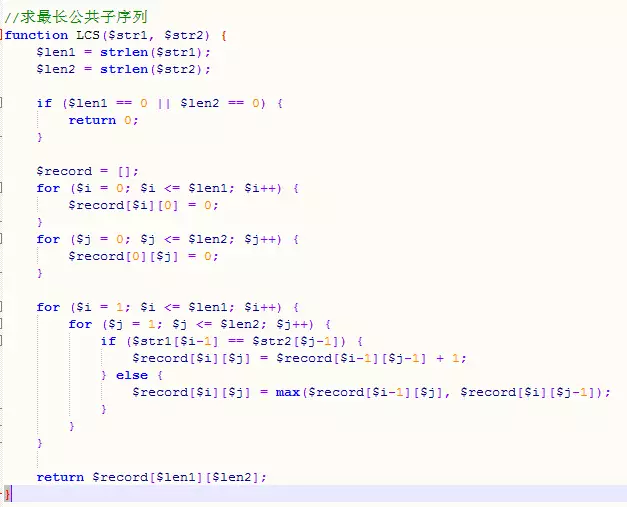
1. Longest common subsequence (string related)

Given two strings, find the longest common subsequence (LCS) and return the length of LCS. For example:
For example: given "ABCD" and "EDCA", the LCS is "A" (or D or C), return 1;
Given "ABCD" and "EACB", the LCS is " AC" returns 2.

Idea: String a of length m and string b of length n, their longest common subsequence longest[m][n] can be passed through a and n-1 of length m-1 The length b is deduced: when a[m] is equal to b[n], longest[m][n] = longest[m-1][n-1] + 1; when a[m] is not equal to b[ n], longest[m][n]=max(longest[m-1][n], longest[m][n-1]). When string a or b is an empty string, the longest common subsequence between it and the other string must be 0. The solution to the final question is longest[strlen(a)][strlen(b)].
Code:

2. Edit distance (string related)

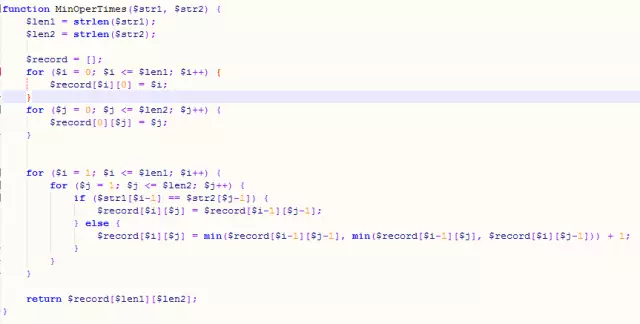
Given two words word1 and word2, calculate word1 to The minimum number of operations for word2.
You have three operation methods in total: insert a character, delete a character, and replace a character.
For example: given work1="mart" and work2="karma", return 3.

Idea: For a string a of length m and a string b of length n (both m and n are greater than 0), if a[m] is not equal to b[n], then a becomes b The minimum number of operations = min (the minimum number of operations for a[m-1] to become b[n]+1, the minimum number of operations for a[m] to become b[n-1]+1, a[m-1 ] becomes the minimum number of operations of b[n-1]); if a[m] is equal to b[n], then the minimum number of operations of a[m] to become b[n] = a[m-1] becomes The minimum number of operations for b[n-1].
Code:

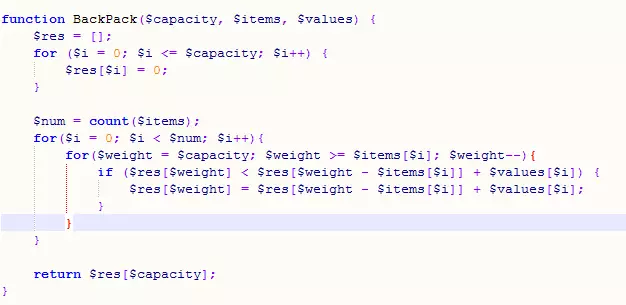
3. Knapsack problem

Given the volume A[i] and value V[i] of n items, What is the maximum total value that they can put into a backpack of size m?
For example: For the item volume [2, 3, 5, 7] and the corresponding value [1, 5, 2, 4], assuming the backpack size is 10, the maximum value that can be loaded is 9.

Idea: When the space is v, for any item i, if i can be put in (v is greater than or equal to weight[i]), then the value f(v) of the v space at this time is equal to f(v -weight[i]) + values[i], so by traversing all items you can find the maximum value that can be obtained when the space is v.
Code:

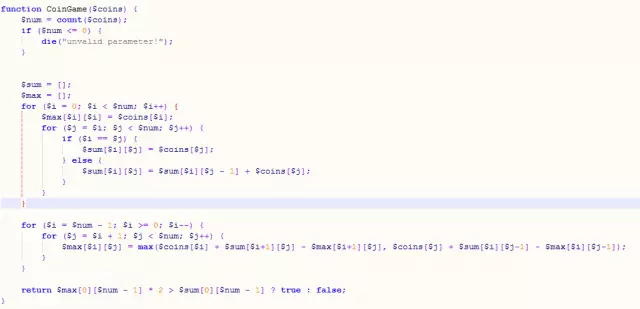
4. Interval problem (Google interview question)

There are n coins arranged in a line, each coin has a different the value of. The two contestants take turns taking a coin from either side until there are no coins left. The total value of the coins obtained is calculated, and the one with the highest value wins. Please decide whether the first player loses or wins?
For example: given the array [3,2,2], return true; given the array [1,20,15], return false.

Idea: For a given closed interval (i to j, j is greater than or equal to i), player A has only two ways to take the coin, from the left or from the right. If you take it from the left, then the maximum face value that A can get = the face value of the coin you get + the total face value of the remaining interval - the maximum face value that player B can get in the remaining interval; the situation where A takes it from the right is different from the case where A takes it from the left Take similar. From this we can get the state transition equation. Through two loops, we can get the total face value of any interval from i to j in the sequence of length n, as well as the maximum value obtained by the first player when j=i (that is, the face value of the i-th coin).
Code:

The above is the content of PHP algorithm learning dynamic programming (2). For more related content, please pay attention to the PHP Chinese website (www.php.cn )!