
This article mainly introduces the multiple linear regression simulation curve algorithm based on PHP. It analyzes the principle of the multiple linear regression simulation curve algorithm and related PHP implementation skills based on specific examples. Friends who need it can refer to it. I hope it can help. Everyone.
Multiple linear regression model: y = b1x1 + b2x2 + b3x3 +... +bnxn;
We are based on a set of data: similar arr_x = [[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [11, 12, 13, 14, 15]]; arr_y = [5, 10, 15]; What we finally want is an array, including from b1 to bn;
Method: Use the least squares method
Formula: 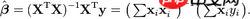 We only use the first half of the formula, That is to use a matrix to calculate
We only use the first half of the formula, That is to use a matrix to calculate
X in the formula is arr_x, we can regard the two-dimensional array as a matrix, y in the formula is arr_y, and also regard it as a matrix (5, 10 , 15) , but it should be written vertically.
Then according to the formula, we will find that we need to use matrix multiplication, transposition, and inversion; so the following codes are given one by one:
public function get_complement($data, $i, $j) {
/* x和y为矩阵data的行数和列数 */
$x = count($data);
$y = count($data[0]);
/* data2为所求剩余矩阵 */
$data2 =[];
for ($k = 0; $k < $x -1; $k++) {
if ($k < $i) {
for ($kk = 0; $kk < $y -1; $kk++) {
if ($kk < $j) {
$data2[$k][$kk] = $data[$k][$kk];
} else {
$data2[$k][$kk] = $data[$k][$kk +1];
}
}
} else {
for ($kk = 0; $kk < $y -1; $kk++) {
if ($kk < $j) {
$data2[$k][$kk] = $data[$k +1][$kk];
} else {
$data2[$k][$kk] = $data[$k +1][$kk +1];
}
}
}
}
return $data2;
}
/* 计算矩阵行列式 */
public function cal_det($data) {
$ans = 0;
if (count($data[0]) === 2) {
$ans = $data[0][0] * $data[1][1] - $data[0][1] * $data[1][0];
} else {
for ($i = 0; $i < count($data[0]); $i++) {
$data_temp = $this->get_complement($data, 0, $i);
if ($i % 2 === 0) {
$ans = $ans + $data[0][$i] * ($this->cal_det($data_temp));
} else {
$ans = $ans - $data[0][$i] * ($this->cal_det($data_temp));
}
}
}
return $ans;
}
/*计算矩阵的伴随矩阵*/
public function ajoint($data) {
$m = count($data);
$n = count($data[0]);
$data2 =[];
for ($i = 0; $i < $m; $i++) {
for ($j = 0; $j < $n; $j++) {
if (($i + $j) % 2 === 0) {
$data2[$i][$j] = $this->cal_det($this->get_complement($data, $i, $j));
} else {
$data2[$i][$j] = - $this->cal_det($this->get_complement($data, $i, $j));
}
}
}
return $this->trans($data2);
}
/*转置矩阵*/
public function trans($data) {
$i = count($data);
$j = count($data[0]);
$data2 =[];
for ($k2 = 0; $k2 < $j; $k2++) {
for ($k1 = 0; $k1 < $i; $k1++) {
$data2[$k2][$k1] = $data[$k1][$k2];
}
}
/*将矩阵转置便可得到伴随矩阵*/
return $data2;
}
/*求矩阵的逆,输入参数为原矩阵*/
public function inv($data) {
$m = count($data);
$n = count($data[0]);
$data2 =[];
$det_val = $this->cal_det($data);
$data2 = $this->ajoint($data);
for ($i = 0; $i < $m; $i++) {
for ($j = 0; $j < $n; $j++) {
$data2[$i][$j] = $data2[$i][$j] / $det_val;
}
}
return $data2;
}
/*求两矩阵的乘积*/
public function getProduct($data1, $data2) {
/*$data1 为左乘矩阵*/
$m1 = count($data1);
$n1 = count($data1[0]);
$m2 = count($data2);
$n2 = count($data2[0]);
$data_new =[];
if ($n1 !== $m2) {
return false;
} else {
for ($i = 0; $i <= $m1 -1; $i++) {
for ($k = 0; $k <= $n2 -1; $k++) {
$data_new[$i][$k] = 0;
for ($j = 0; $j <= $n1 -1; $j++) {
$data_new[$i][$k] += $data1[$i][$j] * $data2[$j][$k];
}
}
}
}
return $data_new;
}
/*多元线性方程*/
public function getParams($arr_x, $arr_y) {
$final =[];
$arr_x_t = $this->trans($arr_x);
$result = $this->getProduct($this->getProduct($this->inv($this->getProduct($arr_x_t, $arr_x)), $arr_x_t), $arr_y);
foreach ($result as $key => $val) {
foreach ($val as $_k => $_v) {
$final[] = $_v;
}
}
return $final;
}The last getParams() method is the final method to find the b parameter array. Just pass in a two-dimensional array arr_x and a one-dimensional array arr_y.
This is generally used for big data analysis to simulate and predict the following developments and trends based on big data.
Related recommendations:
Talk about the current situation, prospects and opportunities of drawing curves
php method to draw sine and cosine curves on pictures
The above is the detailed content of Detailed explanation of simulation curve algorithm based on PHP. For more information, please follow other related articles on the PHP Chinese website!




