Recursion on the basis of PHP data structure

This article mainly introduces the recursion on the basis of PHP data structure, which has certain reference value. Now I share it with you. Friends in need can refer to it

What is recursion?

As mentioned before, recursion is a solution that breaks down large problems into small ones. Generally speaking, recursion is called a call to the function itself. It may sound strange to say this, but in fact in recursion the function does have to call itself.

A chestnut

For example, in mathematics, we all know the concept of "factorial". For example, the factorial of 5 is 5*4*3*2*1.

• 5! = 5 * 4!

• 4! = 4 * 3!

• 3! = 3 * 2!

• 2! = 2 * 1!

• 1! = 1 * 0!

• 0! = 1

We can summarize the rule for finding the factorial of n, that is, n! = n * (n -1) !

This reflects recursion. You can find from this that we transformed the factorial of 5 into another small problem step by step.

Characteristics of recursive algorithms

• Every recursive call must be based on a small sub-problem. For example, the factorial of 5 is the factorial of 5 times 4.

• Recursion must have a Base case. For example, the base case of factorial is 0. When the condition is 0, the recursion stops.

• Avoid loop calls during recursion, otherwise the computer will display a stack overflow error in the end.

function factorial(int $n): int
{
    if ($n = 0) {
        return 1;
    }
    
    return $n * factorial($n - 1);
}

Looking at the above code, we can see that we have a basic condition for the solution to the factorial problem, which is that when n is 0, we return 1. If this condition is not met, we return n multiplied by factorial(n), which meets the first and third items of the recursion property. We avoid looping calls because we break each recursive call into a smaller sub-problem of the larger problem. The above algorithm idea can be expressed as:

Recursion Vs iteration

We can also use the iterative method to implement the above recursive code

function factorial(int $n): int
{
    $result = 1;
    
    for ($i = $n; $i > 0; $i--) {
        $result*= $n;
    }
    
    return $result;
}

If a problem can be very It's easy to use iteration to solve, why do we use recursion?

Recursion is used to deal with more complex problems. Not all problems can be solved simply using iteration. Recursion uses function calls to manage the call stack, so recursion uses more time and memory than iteration. Furthermore, in iteration, we will have a result at each step, but in recursion we have to wait until the base case execution ends before we have any result. Looking at the above example, we find that in the recursive algorithm we do not have any variables or declarations to save the results, while in the iterative algorithm we use $result to save the returned results each time.

Fibonacci Sequence

In mathematics, the Fibonacci Sequence is a special integer sequence. Each number in the sequence is generated by the sum of two other numbers. . The rules are as follows:

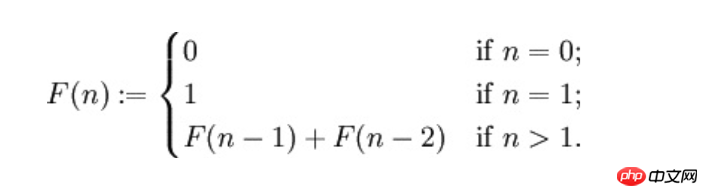
function fibonacci($n)
{
    if ($n == 0) {
        return 0;
    }
    
    if ($n == 1) {
        return 1;
    }
    
    return fibonacci($n - 1) + fibonacci($ - 2);
}

Greatest Common Factor

Another common problem using recursive algorithms is to find the greatest common factor of two numbers.

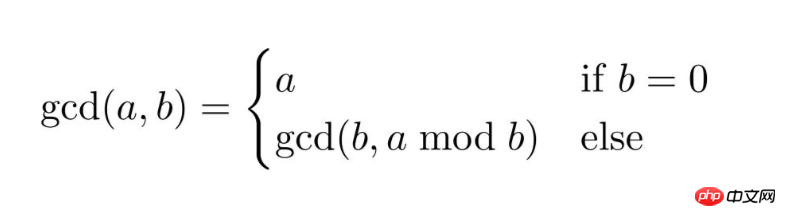
function gcd(int $a, int $b)
{
    if ($b == 0) {
        return $a;
    }
    
    return gcd($b, $a % $b);
}

Recursion type

• Linear recursion

In every recursive call , the function only calls itself once, which is called linear recursion.

• Biary recursion

In binary recursion, each recursive call to the function calls itself twice. The algorithm for solving the Fibonacci sequence is binary recursion. In addition, binary search, divide and conquer algorithm, merge sort, etc. also use binary recursion.

• Tail recursion

When a recursion returns without waiting for operations, it is called tail recursion. In the Fibonacci algorithm, the return value needs to be multiplied by the return value of the previous recursion, so it is not tail recursive, and the algorithm for solving the greatest common factor is tail recursive. Tail recursion is a form of linear recursion.

• Mutual recursion

For example, in each recursive call, A() calls B(), and B() calls A(). Such recursion is called mutual recursion.

• Nested recursion

When a recursive function calls itself recursively as a parameter, it is called nested recursion. A common example is the Ackerman function, see the expression below.

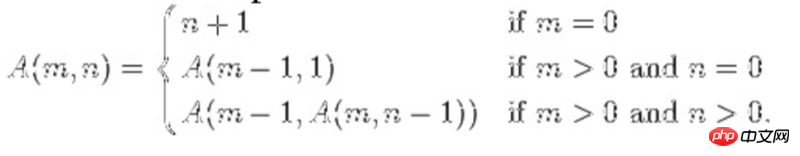
#Looking at the last line, you can see that the second parameter is the recursive function itself.

Next section

The next article will use recursion to solve some problems encountered in actual development, such as building N-level classifications, building nested comments, traversing directory files, etc. .

The above is the entire content of this article. I hope it will be helpful to everyone's study. For more related content, please pay attention to the PHP Chinese website!

Related recommendations:

How to obtain the real IP address of the client in PHP

How to use Elasticsearch in PHP

The above is the detailed content of Recursion on the basis of PHP data structure. For more information, please follow other related articles on the PHP Chinese website!