Backend Development
Python Tutorial
Python ideas and code examples for using iterators to print spiral matrices
Python ideas and code examples for using iterators to print spiral matrices
Thoughts
A spiral matrix refers to a matrix in a spiral shape. Its numbers continue to get larger from the first row to the right and downwards,
It gets bigger to the left, gets bigger up, and so on.
The spiral matrix is represented by a two-dimensional array, with coordinates (x, y), that is (x-axis coordinate, y-axis coordinate).
The direction of the clockwise spiral is ->right, down, left, and up. The numerical expression is x plus 1 grid (1,0), y plus 1 grid (0,1), x minus 1 grid (-1, 0), y minus 1 grid (0,-1).
The coordinates start walking from (0,0), and switch directions when out of range or encountering obstacles.
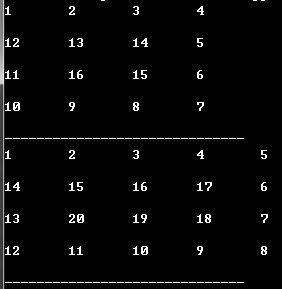
To print a spiral matrix, you first need to assign a value to the n*n array. According to the rules, it can be seen that each layer is incremented in the order of right->bottom->left->top. Therefore, as long as you find The first number of each layer is enough. The first value is the first number of the previous layer + 4*n-4. During the loop, n decreases by 2 each time.
Code
After the above analysis, the idea is very clear, a thousand words are not worth a code:
import itertools
def spiral(n,m):
_status = itertools.cycle(['right','down','left','up'])#用于状态周期性的切换
_movemap = {
'right':(1,0),
'down':(0,1),
'left':(-1,0),
'up':(0,-1),
}
pos2no = dict.fromkeys([(x,y) for x in range(n) for y in range(m)])
_pos = (0,0)
_st = next(_status)
for i in range(1,n*m+1):
_oldpos = _pos
_pos = tuple(map(sum,zip(_pos,_movemap[_st])))#根据状态进行移动
if (_pos not in pos2no) or (pos2no[_pos]):#当超出范围或遇到障碍时切换方向
_st = next(_status)
_pos = tuple(map(sum,zip(_oldpos,_movemap[_st])))
pos2no[_oldpos] = i
return pos2no
def display_spiral(n,m):
pos2no = spiral(n,m)
for i in range(m):
for j in range(n):
print pos2no[(j,i)],'\t',
print '\n'
print '-'*30
display_spiral(4,4)
display_spiral(5,4)
Hot AI Tools
Undresser.AI Undress
AI-powered app for creating realistic nude photos
AI Clothes Remover
Online AI tool for removing clothes from photos.
Undress AI Tool
Undress images for free
Clothoff.io
AI clothes remover
Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!
Hot Article
Hot Tools
Notepad++7.3.1
Easy-to-use and free code editor
SublimeText3 Chinese version
Chinese version, very easy to use
Zend Studio 13.0.1
Powerful PHP integrated development environment
Dreamweaver CS6
Visual web development tools
SublimeText3 Mac version
God-level code editing software (SublimeText3)
Hot Topics
1662
14
1419
52
1313
25
1262
29
1235
24
PHP and Python: Different Paradigms Explained
Apr 18, 2025 am 12:26 AM
PHP is mainly procedural programming, but also supports object-oriented programming (OOP); Python supports a variety of paradigms, including OOP, functional and procedural programming. PHP is suitable for web development, and Python is suitable for a variety of applications such as data analysis and machine learning.
Choosing Between PHP and Python: A Guide
Apr 18, 2025 am 12:24 AM
PHP is suitable for web development and rapid prototyping, and Python is suitable for data science and machine learning. 1.PHP is used for dynamic web development, with simple syntax and suitable for rapid development. 2. Python has concise syntax, is suitable for multiple fields, and has a strong library ecosystem.
PHP and Python: A Deep Dive into Their History
Apr 18, 2025 am 12:25 AM
PHP originated in 1994 and was developed by RasmusLerdorf. It was originally used to track website visitors and gradually evolved into a server-side scripting language and was widely used in web development. Python was developed by Guidovan Rossum in the late 1980s and was first released in 1991. It emphasizes code readability and simplicity, and is suitable for scientific computing, data analysis and other fields.
Python vs. JavaScript: The Learning Curve and Ease of Use
Apr 16, 2025 am 12:12 AM
Python is more suitable for beginners, with a smooth learning curve and concise syntax; JavaScript is suitable for front-end development, with a steep learning curve and flexible syntax. 1. Python syntax is intuitive and suitable for data science and back-end development. 2. JavaScript is flexible and widely used in front-end and server-side programming.
How to run sublime code python
Apr 16, 2025 am 08:48 AM
To run Python code in Sublime Text, you need to install the Python plug-in first, then create a .py file and write the code, and finally press Ctrl B to run the code, and the output will be displayed in the console.
Where to write code in vscode
Apr 15, 2025 pm 09:54 PM
Writing code in Visual Studio Code (VSCode) is simple and easy to use. Just install VSCode, create a project, select a language, create a file, write code, save and run it. The advantages of VSCode include cross-platform, free and open source, powerful features, rich extensions, and lightweight and fast.
Can visual studio code be used in python
Apr 15, 2025 pm 08:18 PM
VS Code can be used to write Python and provides many features that make it an ideal tool for developing Python applications. It allows users to: install Python extensions to get functions such as code completion, syntax highlighting, and debugging. Use the debugger to track code step by step, find and fix errors. Integrate Git for version control. Use code formatting tools to maintain code consistency. Use the Linting tool to spot potential problems ahead of time.
How to run python with notepad
Apr 16, 2025 pm 07:33 PM
Running Python code in Notepad requires the Python executable and NppExec plug-in to be installed. After installing Python and adding PATH to it, configure the command "python" and the parameter "{CURRENT_DIRECTORY}{FILE_NAME}" in the NppExec plug-in to run Python code in Notepad through the shortcut key "F6".
