 Backend Development
Backend Development
 Python Tutorial
Python Tutorial
 Example of building a simple neural network on PyTorch to implement regression and classification
Example of building a simple neural network on PyTorch to implement regression and classification
Example of building a simple neural network on PyTorch to implement regression and classification
This article mainly introduces examples of building a simple neural network on PyTorch to implement regression and classification. Now I share it with you and give it as a reference. Let’s take a look together
This article introduces an example of building a simple neural network on PyTorch to implement regression and classification. I would like to share it with you. The details are as follows:

1. Getting started with PyTorch
1. Installation method
Log in to the PyTorch official website, http://pytorch.org, you can See the following interface:
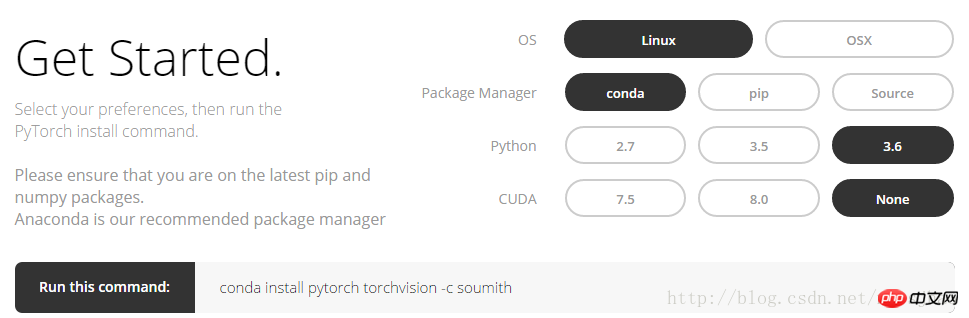
After selecting the option in the picture above, you can get the conda command under Linux:
conda install pytorch torchvision -c soumith
Currently PyTorch only supports MacOS and Linux, and does not support Windows yet. Installing PyTorch will install two modules, one is torch and the other is torchvision. Torch is the main module, which is used to build neural networks. torchvision is the auxiliary module, which has a database and some already trained neural networks waiting for you to use directly. For example (VGG, AlexNet, ResNet).
2. Numpy and Torch
torch_data = torch.from_numpy(np_data) can convert numpy(array) format to torch(tensor) format; torch_data.numpy( ) can also convert the tensor format of torch to the array format of numpy. Note that Torch's Tensor and numpy's array will share their storage space, and modifying one will cause the other to be modified.
For 1-dimensional (1-D) data, numpy prints output in the form of row vectors, while torch prints output in the form of column vectors.
Other functions in numpy such as sin, cos, abs, mean, etc. can be used in the same way in torch. It should be noted that matrix multiplication of np.matmul(data, data) and data.dot(data) in numpy will yield the same result; torch.mm(tensor, tensor) in torch is a matrix multiplication method, resulting in a matrix , tensor.dot(tensor) will convert the tensor into a 1-dimensional tensor, then multiply it element by element and sum it up to get a real number.
Related code:
import torch import numpy as np np_data = np.arange(6).reshape((2, 3)) torch_data = torch.from_numpy(np_data) # 将numpy(array)格式转换为torch(tensor)格式 tensor2array = torch_data.numpy() print( '\nnumpy array:\n', np_data, '\ntorch tensor:', torch_data, '\ntensor to array:\n', tensor2array, ) # torch数据格式在print的时候前后自动添加换行符 # abs data = [-1, -2, 2, 2] tensor = torch.FloatTensor(data) print( '\nabs', '\nnumpy: \n', np.abs(data), '\ntorch: ', torch.abs(tensor) ) # 1维的数据,numpy是行向量形式显示,torch是列向量形式显示 # sin print( '\nsin', '\nnumpy: \n', np.sin(data), '\ntorch: ', torch.sin(tensor) ) # mean print( '\nmean', '\nnumpy: ', np.mean(data), '\ntorch: ', torch.mean(tensor) ) # 矩阵相乘 data = [[1,2], [3,4]] tensor = torch.FloatTensor(data) print( '\nmatrix multiplication (matmul)', '\nnumpy: \n', np.matmul(data, data), '\ntorch: ', torch.mm(tensor, tensor) ) data = np.array(data) print( '\nmatrix multiplication (dot)', '\nnumpy: \n', data.dot(data), '\ntorch: ', tensor.dot(tensor) )
##3. Variable
PyTorch The neural network in comes from the autograd package, which provides automatic derivation methods for all operations of Tensor. autograd.Variable This is the core class in this package. Variable can be understood as a container containing tensor, which wraps a Tensor and supports almost all operations defined on it. Once the operation is completed, .backward() can be called to automatically calculate all gradients. In other words, only by placing the tensor in Variable can operations such as reverse transfer and automatic derivation be implemented in the neural network. The original tensor can be accessed through the attribute .data, and the gradient of this Variable can be viewed through the .grad attribute.Related codes:
import torch from torch.autograd import Variable tensor = torch.FloatTensor([[1,2],[3,4]]) variable = Variable(tensor, requires_grad=True) # 打印展示Variable类型 print(tensor) print(variable) t_out = torch.mean(tensor*tensor) # 每个元素的^ 2 v_out = torch.mean(variable*variable) print(t_out) print(v_out) v_out.backward() # Variable的误差反向传递 # 比较Variable的原型和grad属性、data属性及相应的numpy形式 print('variable:\n', variable) # v_out = 1/4 * sum(variable*variable) 这是计算图中的 v_out 计算步骤 # 针对于 v_out 的梯度就是, d(v_out)/d(variable) = 1/4*2*variable = variable/2 print('variable.grad:\n', variable.grad) # Variable的梯度 print('variable.data:\n', variable.data) # Variable的数据 print(variable.data.numpy()) #Variable的数据的numpy形式
variable:
Variable containing:4. Activation function activationfunction1 2
3 4
[torch.FloatTensor of size 2x2]
variable.grad:
Variable containing:
0.5000 1.0000
1.5000 2.0000
[torch.FloatTensor of size 2x2]
variable.data:
1 2
3 4
[torch.FloatTensor of size 2x2]
[[ 1 . 2.]
[ 3. 4.]]
Torch’s activation functions are all in torch.nn. In functional, relu, sigmoid, tanh, softplus are all commonly used excitation functions.
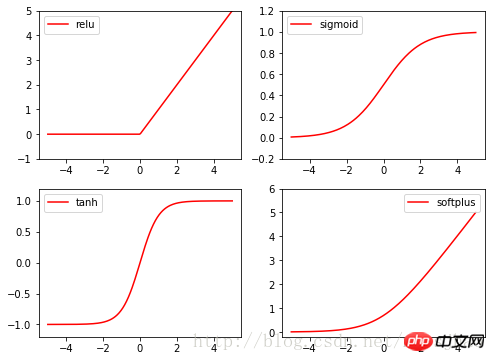
import torch import torch.nn.functional as F from torch.autograd import Variable import matplotlib.pyplot as plt x = torch.linspace(-5, 5, 200) x_variable = Variable(x) #将x放入Variable x_np = x_variable.data.numpy() # 经过4种不同的激励函数得到的numpy形式的数据结果 y_relu = F.relu(x_variable).data.numpy() y_sigmoid = F.sigmoid(x_variable).data.numpy() y_tanh = F.tanh(x_variable).data.numpy() y_softplus = F.softplus(x_variable).data.numpy() plt.figure(1, figsize=(8, 6)) plt.subplot(221) plt.plot(x_np, y_relu, c='red', label='relu') plt.ylim((-1, 5)) plt.legend(loc='best') plt.subplot(222) plt.plot(x_np, y_sigmoid, c='red', label='sigmoid') plt.ylim((-0.2, 1.2)) plt.legend(loc='best') plt.subplot(223) plt.plot(x_np, y_tanh, c='red', label='tanh') plt.ylim((-1.2, 1.2)) plt.legend(loc='best') plt.subplot(224) plt.plot(x_np, y_softplus, c='red', label='softplus') plt.ylim((-0.2, 6)) plt.legend(loc='best') plt.show()
Look at the complete code first:
import torch
from torch.autograd import Variable
import torch.nn.functional as F
import matplotlib.pyplot as plt
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # 将1维的数据转换为2维数据
y = x.pow(2) + 0.2 * torch.rand(x.size())
# 将tensor置入Variable中
x, y = Variable(x), Variable(y)
#plt.scatter(x.data.numpy(), y.data.numpy())
#plt.show()
# 定义一个构建神经网络的类
class Net(torch.nn.Module): # 继承torch.nn.Module类
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__() # 获得Net类的超类(父类)的构造方法
# 定义神经网络的每层结构形式
# 各个层的信息都是Net类对象的属性
self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出
self.predict = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出
# 将各层的神经元搭建成完整的神经网络的前向通路
def forward(self, x):
x = F.relu(self.hidden(x)) # 对隐藏层的输出进行relu激活
x = self.predict(x)
return x
# 定义神经网络
net = Net(1, 10, 1)
print(net) # 打印输出net的结构
# 定义优化器和损失函数
optimizer = torch.optim.SGD(net.parameters(), lr=0.5) # 传入网络参数和学习率
loss_function = torch.nn.MSELoss() # 最小均方误差
# 神经网络训练过程
plt.ion() # 动态学习过程展示
plt.show()
for t in range(300):
prediction = net(x) # 把数据x喂给net,输出预测值
loss = loss_function(prediction, y) # 计算两者的误差,要注意两个参数的顺序
optimizer.zero_grad() # 清空上一步的更新参数值
loss.backward() # 误差反相传播,计算新的更新参数值
optimizer.step() # 将计算得到的更新值赋给net.parameters()
# 可视化训练过程
if (t+1) % 10 == 0:
plt.cla()
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
plt.text(0.5, 0, 'L=%.4f' % loss.data[0], fontdict={'size': 20, 'color': 'red'})
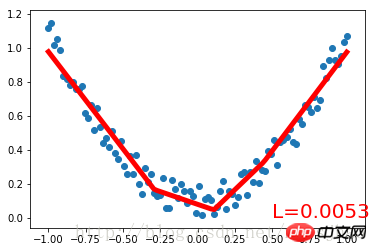
plt.pause(0.1)Run result:
Net (
(hidden): Linear (1 -> 10)(predict): Linear (10 -> 1)
)
三、PyTorch实现简单分类
完整代码:
import torch
from torch.autograd import Variable
import torch.nn.functional as F
import matplotlib.pyplot as plt
# 生成数据
# 分别生成2组各100个数据点,增加正态噪声,后标记以y0=0 y1=1两类标签,最后cat连接到一起
n_data = torch.ones(100,2)
# torch.normal(means, std=1.0, out=None)
x0 = torch.normal(2*n_data, 1) # 以tensor的形式给出输出tensor各元素的均值,共享标准差
y0 = torch.zeros(100)
x1 = torch.normal(-2*n_data, 1)
y1 = torch.ones(100)
x = torch.cat((x0, x1), 0).type(torch.FloatTensor) # 组装(连接)
y = torch.cat((y0, y1), 0).type(torch.LongTensor)
# 置入Variable中
x, y = Variable(x), Variable(y)
class Net(torch.nn.Module):
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(n_feature, n_hidden)
self.out = torch.nn.Linear(n_hidden, n_output)
def forward(self, x):
x = F.relu(self.hidden(x))
x = self.out(x)
return x
net = Net(n_feature=2, n_hidden=10, n_output=2)
print(net)
optimizer = torch.optim.SGD(net.parameters(), lr=0.012)
loss_func = torch.nn.CrossEntropyLoss()
plt.ion()
plt.show()
for t in range(100):
out = net(x)
loss = loss_func(out, y) # loss是定义为神经网络的输出与样本标签y的差别,故取softmax前的值
optimizer.zero_grad()
loss.backward()
optimizer.step()
if t % 2 == 0:
plt.cla()
# 过了一道 softmax 的激励函数后的最大概率才是预测值
# torch.max既返回某个维度上的最大值,同时返回该最大值的索引值
prediction = torch.max(F.softmax(out), 1)[1] # 在第1维度取最大值并返回索引值
pred_y = prediction.data.numpy().squeeze()
target_y = y.data.numpy()
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
accuracy = sum(pred_y == target_y)/200 # 预测中有多少和真实值一样
plt.text(1.5, -4, 'Accu=%.2f' % accuracy, fontdict={'size': 20, 'color': 'red'})
plt.pause(0.1)
plt.ioff()
plt.show()神经网络结构部分的Net类与前文的回归部分的结构相同。
需要注意的是,在循环迭代训练部分,out定义为神经网络的输出结果,计算误差loss时不是使用one-hot形式的,loss是定义在out与y上的torch.nn.CrossEntropyLoss(),而预测值prediction定义为out经过Softmax后(将结果转化为概率值)的结果。
运行结果:
Net (
(hidden): Linear (2 -> 10)
(out):Linear (10 -> 2)
)
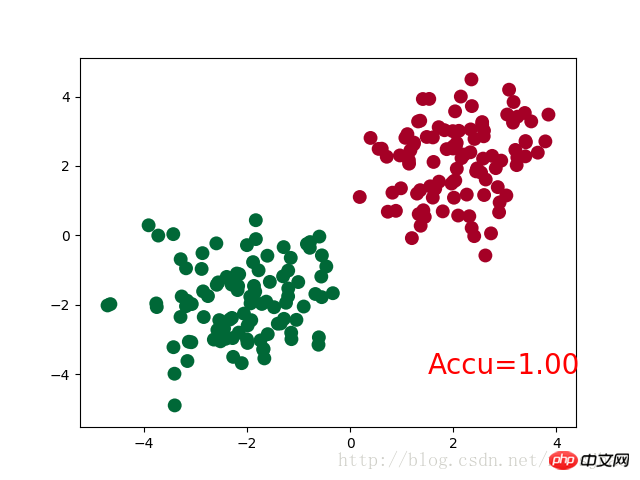
四、补充知识
1. super()函数
在定义Net类的构造方法的时候,使用了super(Net,self).__init__()语句,当前的类和对象作为super函数的参数使用,这条语句的功能是使Net类的构造方法获得其超类(父类)的构造方法,不影响对Net类单独定义构造方法,且不必关注Net类的父类到底是什么,若需要修改Net类的父类时只需修改class语句中的内容即可。
2. torch.normal()
torch.normal()可分为三种情况:(1)torch.normal(means,std, out=None)中means和std都是Tensor,两者的形状可以不必相同,但Tensor内的元素数量必须相同,一一对应的元素作为输出的各元素的均值和标准差;(2)torch.normal(mean=0.0, std, out=None)中mean是一个可定义的float,各个元素共享该均值;(3)torch.normal(means,std=1.0, out=None)中std是一个可定义的float,各个元素共享该标准差。
3. torch.cat(seq, dim=0)
torch.cat可以将若干个Tensor组装连接起来,dim指定在哪个维度上进行组装。
4. torch.max()
(1)torch.max(input)→ float
input是tensor,返回input中的最大值float。
(2)torch.max(input,dim, keepdim=True, max=None, max_indices=None) -> (Tensor, LongTensor)
同时返回指定维度=dim上的最大值和该最大值在该维度上的索引值。
相关推荐:
The above is the detailed content of Example of building a simple neural network on PyTorch to implement regression and classification. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1666
1666
 14
14
 1425
1425
 52
52
 1327
1327
 25
25
 1273
1273
 29
29
 1252
1252
 24
24
 The perfect combination of PyCharm and PyTorch: detailed installation and configuration steps
Feb 21, 2024 pm 12:00 PM
The perfect combination of PyCharm and PyTorch: detailed installation and configuration steps
Feb 21, 2024 pm 12:00 PM
PyCharm is a powerful integrated development environment (IDE), and PyTorch is a popular open source framework in the field of deep learning. In the field of machine learning and deep learning, using PyCharm and PyTorch for development can greatly improve development efficiency and code quality. This article will introduce in detail how to install and configure PyTorch in PyCharm, and attach specific code examples to help readers better utilize the powerful functions of these two. Step 1: Install PyCharm and Python
 YOLO is immortal! YOLOv9 is released: performance and speed SOTA~
Feb 26, 2024 am 11:31 AM
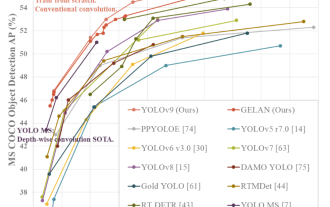
YOLO is immortal! YOLOv9 is released: performance and speed SOTA~
Feb 26, 2024 am 11:31 AM
Today's deep learning methods focus on designing the most suitable objective function so that the model's prediction results are closest to the actual situation. At the same time, a suitable architecture must be designed to obtain sufficient information for prediction. Existing methods ignore the fact that when the input data undergoes layer-by-layer feature extraction and spatial transformation, a large amount of information will be lost. This article will delve into important issues when transmitting data through deep networks, namely information bottlenecks and reversible functions. Based on this, the concept of programmable gradient information (PGI) is proposed to cope with the various changes required by deep networks to achieve multi-objectives. PGI can provide complete input information for the target task to calculate the objective function, thereby obtaining reliable gradient information to update network weights. In addition, a new lightweight network framework is designed
 Introduction to five sampling methods in natural language generation tasks and Pytorch code implementation
Feb 20, 2024 am 08:50 AM
Introduction to five sampling methods in natural language generation tasks and Pytorch code implementation
Feb 20, 2024 am 08:50 AM
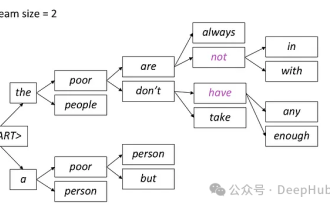
In natural language generation tasks, sampling method is a technique to obtain text output from a generative model. This article will discuss 5 common methods and implement them using PyTorch. 1. GreedyDecoding In greedy decoding, the generative model predicts the words of the output sequence based on the input sequence time step by time. At each time step, the model calculates the conditional probability distribution of each word, and then selects the word with the highest conditional probability as the output of the current time step. This word becomes the input to the next time step, and the generation process continues until some termination condition is met, such as a sequence of a specified length or a special end marker. The characteristic of GreedyDecoding is that each time the current conditional probability is the best
 How to implement dual WeChat login on Huawei mobile phones?
Mar 24, 2024 am 11:27 AM
How to implement dual WeChat login on Huawei mobile phones?
Mar 24, 2024 am 11:27 AM
How to implement dual WeChat login on Huawei mobile phones? With the rise of social media, WeChat has become one of the indispensable communication tools in people's daily lives. However, many people may encounter a problem: logging into multiple WeChat accounts at the same time on the same mobile phone. For Huawei mobile phone users, it is not difficult to achieve dual WeChat login. This article will introduce how to achieve dual WeChat login on Huawei mobile phones. First of all, the EMUI system that comes with Huawei mobile phones provides a very convenient function - dual application opening. Through the application dual opening function, users can simultaneously
 so fast! Recognize video speech into text in just a few minutes with less than 10 lines of code
Feb 27, 2024 pm 01:55 PM
so fast! Recognize video speech into text in just a few minutes with less than 10 lines of code
Feb 27, 2024 pm 01:55 PM
Hello everyone, I am Kite. Two years ago, the need to convert audio and video files into text content was difficult to achieve, but now it can be easily solved in just a few minutes. It is said that in order to obtain training data, some companies have fully crawled videos on short video platforms such as Douyin and Kuaishou, and then extracted the audio from the videos and converted them into text form to be used as training corpus for big data models. If you need to convert a video or audio file to text, you can try this open source solution available today. For example, you can search for the specific time points when dialogues in film and television programs appear. Without further ado, let’s get to the point. Whisper is OpenAI’s open source Whisper. Of course it is written in Python. It only requires a few simple installation packages.
 Tutorial on installing PyCharm with PyTorch
Feb 24, 2024 am 10:09 AM
Tutorial on installing PyCharm with PyTorch
Feb 24, 2024 am 10:09 AM
As a powerful deep learning framework, PyTorch is widely used in various machine learning projects. As a powerful Python integrated development environment, PyCharm can also provide good support when implementing deep learning tasks. This article will introduce in detail how to install PyTorch in PyCharm and provide specific code examples to help readers quickly get started using PyTorch for deep learning tasks. Step 1: Install PyCharm First, we need to make sure we have
 PHP Programming Guide: Methods to Implement Fibonacci Sequence
Mar 20, 2024 pm 04:54 PM
PHP Programming Guide: Methods to Implement Fibonacci Sequence
Mar 20, 2024 pm 04:54 PM
The programming language PHP is a powerful tool for web development, capable of supporting a variety of different programming logics and algorithms. Among them, implementing the Fibonacci sequence is a common and classic programming problem. In this article, we will introduce how to use the PHP programming language to implement the Fibonacci sequence, and attach specific code examples. The Fibonacci sequence is a mathematical sequence defined as follows: the first and second elements of the sequence are 1, and starting from the third element, the value of each element is equal to the sum of the previous two elements. The first few elements of the sequence
 1.3ms takes 1.3ms! Tsinghua's latest open source mobile neural network architecture RepViT
Mar 11, 2024 pm 12:07 PM
1.3ms takes 1.3ms! Tsinghua's latest open source mobile neural network architecture RepViT
Mar 11, 2024 pm 12:07 PM
Paper address: https://arxiv.org/abs/2307.09283 Code address: https://github.com/THU-MIG/RepViTRepViT performs well in the mobile ViT architecture and shows significant advantages. Next, we explore the contributions of this study. It is mentioned in the article that lightweight ViTs generally perform better than lightweight CNNs on visual tasks, mainly due to their multi-head self-attention module (MSHA) that allows the model to learn global representations. However, the architectural differences between lightweight ViTs and lightweight CNNs have not been fully studied. In this study, the authors integrated lightweight ViTs into the effective



