c++ - 特林斯公式如何计算N！ 的最高位

Question

如果是一个非常大的N <10000000 那么计算出来的N！也是非常大的，现在只需要知道最高位的数字。
通过斯特林公式可以计算。
特林斯公式：
（公式1）
如下是算法：

result = 0.5* log(2*PI*(double)n)/log(10.0) + (double)n* log((double)n/E)/log(10.0);
result -= (int)result;
first_number = exp(result * log(10.0));

以上算法代码计算通过公式表示：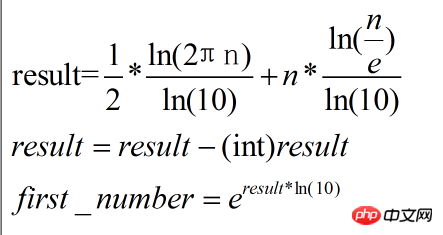
（公式2）
目前已知通过如下计算可以得到最高位：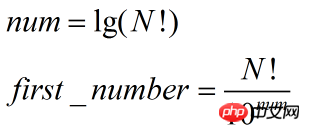
（公式3）
剩下的就是求N！，虽然N！可以通过特林斯计算，但是计算结果非常大。计算机直接计算会溢出结果，如下执行结果：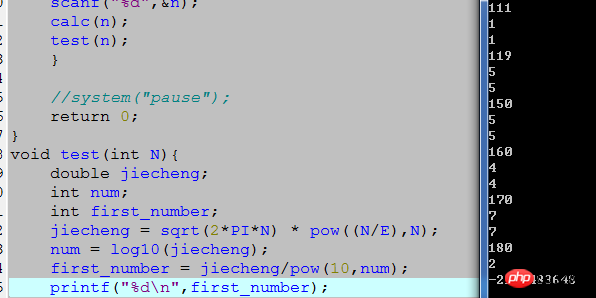

可以看出当执行到180的时候结果都已经溢出。
原因应该是在计算N！ 的时候结果直接存储在计算机导致空间不足。
我所不明白的是为什么（公式2）的算法就可以直接计算出结果不溢出，且正确（当然数字过小的话也会有错误，比如0,1,2,3,7,8结果将不正确）。

Answer 1

Finally, the highest position is found through the logarithm with base 10 log10(xxx). Do you understand this? The above is to convert the logarithm with base 10 into the logarithm with base e through logarithmic transformation aka: ln(yyy)

Answer 2

First of all, Mr. Beard has made it very clear. The principle is what he said. The original problem solved by lg is converted into ln.

I’d better post a picture for you: (Those who like mathematics are good)

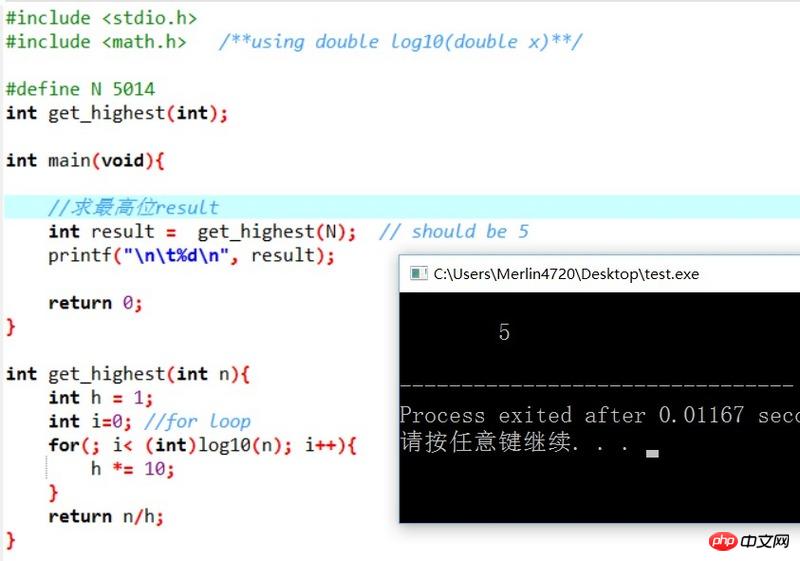
See, in fact, the above has been verified. If the highest bit of 5014 is required, then it can be written as:
The highest bit = 5014 / (taking an integer) 1g(5014); (Note that in C-like languages, division , integer truncation will be performed)

ok, let’s get down to business, your Trins formula, assuming that the approximate value of the factorial obtained is

If you want to get the highest digit h of this number, then there is the following calculation:

h = X / (int)lgX;

At this time, X has been obtained through Trins formula,

Just calculate the "integer part of lgX".

First do the calculation in a general way (don’t calculate the whole part and decimal part first, just calculate lgX directly)

lgX = lnX / ln10 (This is the formula you brought in Trins formula to evaluate, oh, your diagram is wrong)

Get lgX= result (I simplified it, If you don’t believe me, just simplify that Trins formula into)

At this point, you understand that by getting the integer part of result, you can rescue the integer part of lgX, and you can also find the highest bit h.

Instead of "getting the decimal part" as you said.

Finally, according to the Trins formula you provided, the value of factorial is:

X is approximately equal to e^(ln10 * the integer part of result); (You can transform it from Trins formula to Take a look at this step)

It doesn’t seem to be what you said

first_number = exp(result * log(10.0));

Any more questions? Are you discussing? Post your final results?