用JavaScript實作用一個DIV來包裝文字元素節點_javascript技巧
當你的應用需要依賴某個特定的JavaScript類別庫時,你無意中總是會試圖解決某些類別庫自身的問題,而不是語言的問題。就例如當我試著將文字(可能也包含HTML元素)用一個DIV元素包起來時。假設有以下HTML:
This is some text and <a href="">a link</a>
這時候如果想把它轉換成下面這樣:
<div>This is some text and <a href="">a link</a><div>
最簡單暴力的方法是,你可以在父元素上通過 .innerHTML 屬性來執行更新,但問題是這樣一來所有綁定的事件監聽都會失效,因為使用 innerHTML 時會重新創建一個HTML元素。這真是個大玻璃杯!所以這時候只能利用JavaScript來實現 —— 尺有所短、寸有所長。下面是實作程式碼:
var newWrapper = document.createElement('div');
while(existingParent.firstChild) {
// 移动DOM元素,不会创建新元素
newWrapper.appendChild(existingParent.firstChild);
}這裡不能使用for迴圈,因為 childNodes 是一個動態節點組成的集合,只要移動節點就會影響到他的index索引值。我們用while循環一直偵測父元素的 firstChild ,如果其傳回一個代表 false 的值, 那麼你就知道所有的節點都已經移到新的parent中了!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

熱門話題
 使用SWIG將C/C++包裝為Python
Aug 25, 2023 pm 08:25 PM
使用SWIG將C/C++包裝為Python
Aug 25, 2023 pm 08:25 PM
有多種方法可以將現有的C或C++功能封裝在Python中。在本節中,我們將了解如何使用SWIG包裝C/C++功能。以下是在python中包裝C/C++功能的其他選項。手動包裝使用Pyrex包裝C代碼。 CtypesSIPBoostPythonSWIG(簡單包裝介面產生器)能夠使用許多其他語言(包括Perl、Python、PHP、Ruby、Tcl、C#、CommonLisp(CLISP、Allegro、CL、UFFI、CFFI)、Java、Modula-3和OCAML。Swig還支援多種解釋和編譯的
 查詢從節點X開始,距離最多為D的子樹中的最小權重
Aug 25, 2023 am 11:25 AM
查詢從節點X開始,距離最多為D的子樹中的最小權重
Aug 25, 2023 am 11:25 AM
在進行電腦程式設計時,有時需要求出源自特定節點的子樹的最小權重,條件是該子樹不能包含距離指定節點超過D個單位的節點。這個問題出現在各個領域和應用中,包括圖論、基於樹的演算法和網路最佳化。子樹是較大樹結構的子集,指定的節點作為子樹的根節點。子樹包含根節點的所有後代及其連接邊。節點的權重是指分配給該節點的特定值,可以表示其重要性、重要性或其他相關指標。在這個問題中,目標是找到子樹中所有節點中的最小權重,同時將子樹限制在距離根節點最多D個單位的節點。在下面的文章中,我們將深入研究從子樹中挖掘最小權重的複雜性
 如何透過Vue和jsmind實現心智圖的節點複製和剪切功能?
Aug 15, 2023 pm 05:57 PM
如何透過Vue和jsmind實現心智圖的節點複製和剪切功能?
Aug 15, 2023 pm 05:57 PM
如何透過Vue和jsmind實現心智圖的節點複製和剪切功能?心智圖是一種常見的思考工具,能夠幫助我們整理想法、梳理思考邏輯。而節點複製和剪切功能是心智圖中常用的操作,能讓我們更方便重複利用現有的節點,提高思考整理的效率。在本文中,我們將使用Vue和jsmind這兩個工具來實現心智圖的節點複製和剪切功能。首先,我們需要安裝Vue和jsmind,並創建
 js刪除節點的方法是什麼
Sep 01, 2023 pm 05:00 PM
js刪除節點的方法是什麼
Sep 01, 2023 pm 05:00 PM
js刪除節點的方法有:1、removeChild()方法,用於從父節點移除指定的子節點,它需要兩個參數,第一個參數是要刪除的子節點,第二個參數是父節點;2、parentNode.removeChild()方法,可以直接透過父節點呼叫來刪除子節點;3、remove()方法,可以直接刪除節點,而無需指定父節點;4、innerHTML屬性,用於刪除節點的內容。
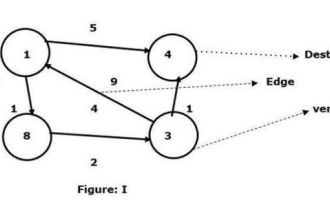 使用佛洛伊德-沃沙爾演算法找到任兩個節點之間的最短路徑
Sep 20, 2023 pm 02:21 PM
使用佛洛伊德-沃沙爾演算法找到任兩個節點之間的最短路徑
Sep 20, 2023 pm 02:21 PM
C++有一個宏,它被定義為一段程式碼或期望的值,並且每當使用者需要時,它將被重複使用。佛洛伊德-沃爾夏爾演算法是在給定的加權圖中找到所有頂點對之間最短路徑的過程。該演算法遵循動態規劃的方法來找到最小權重圖。讓我們透過圖表來理解佛洛伊德-沃爾夏爾演算法的意義-以頂點1為來源,頂點4為目的地,求它們之間的最短路徑。我們已經看到有兩條路徑可以連接到目標頂點4。1->4–邊的權重為51->8->3->4–邊權重(1+2+1)為4。在給定的圖I中,我們看到兩個頂點之間連接的最小邊。所以這裡頂點
 檢查給定的圖中兩個節點之間的路徑是否表示最短路徑
Sep 07, 2023 pm 06:57 PM
檢查給定的圖中兩個節點之間的路徑是否表示最短路徑
Sep 07, 2023 pm 06:57 PM
要檢查圖表的兩個中心之間的給定路徑是否符合最短路徑,可以透過使用可靠的最短路徑將沿著給定路徑的整個邊緣權重與相同中心組合之間的最短距離進行比較方式計算,例如Dijkstra計算或Floyd−Warshall計算。如果給定路徑上的所有邊權重與最有限的刪除相匹配,那麼它就代表最簡單的路徑。另外:如果整個邊權重比最短距離更突出,則表示圖表中兩個中心之間存在較短的距離。使用的方法Dijkstra演算法具有邊緣反轉成本的Floyd−Warshall演算法貪心演算法Dijkstra的計算可能是一種流行的圖表遍歷計算
 有了插件的 ChatGPT ,是一個節點,卻不是中心
Apr 04, 2023 am 11:45 AM
有了插件的 ChatGPT ,是一個節點,卻不是中心
Apr 04, 2023 am 11:45 AM
OpenAI 是機器人和機器人對話的世界裡面的一個節點(雖然是一個重要的節點),卻不是中心。 ChatGPT 推出了 Plugin 機制,這是一項非常令人興奮的進展。大家不約而同評價「一個作業系統就此誕生」。這個說法,大錯特錯。 OpenAI 是機器人和機器人對話的世界裡面的一個節點(雖然是一個重要的節點),卻不是中心。我腦中一直有個圖景:一個機器人和機器人對話的世界。人跟一個機器人聊天,讓這個機器人透過它的機器人朋友幫助人類完成任務。 ChatGPT Plugin 嚴絲合縫的示範了這個世界的







