javascript中解析四則運算表達式的演算法與範例_javascript技巧

在寫程式碼時我們有時候會碰到需要自己解析四則運算表達式的情況，本文簡單的介紹使用JavaScript實作對簡單四則運算表達式的解析。

一、熟悉概念

中綴表示法（或中綴記法）是一個通用的算術或邏輯公式表示方法， 操作符是以中綴形式處於操作數的中間（例：3 4）。也就是我們最常用的算術表達式，中綴表達式對人類來說比較容易理解，但不容易電腦解析。

逆波蘭表示法（Reverse Polish notation，RPN，或逆波蘭記法），是一種是由波蘭數學家揚·武卡謝維奇1920年引入的數學表達式方式，在逆波蘭記法中，所有運算子置於操作數的後面，因此也被稱為後綴表示法。逆波蘭記法不需要括號來識別運算元的優先權。逆波蘭表示法容易使用堆疊結構對表達式進行解析計算，所以，這裡我們解析四則元素表達式，是先從中綴表達式，轉換為逆波蘭表達式。然後再計算值。

二、轉換流程

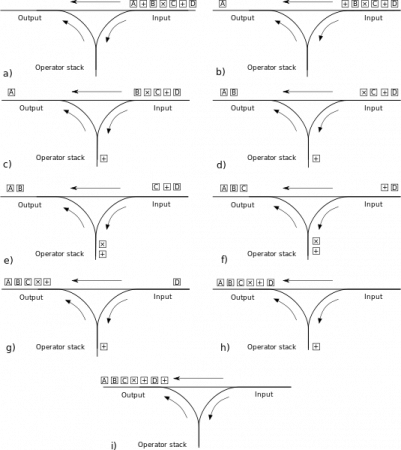
中綴表達式轉換為後綴表達式（調度場演算法）

1.輸入佇列彈出一個記號
2.如果記號為數字，加入輸出佇列
3.如果是操作符（ -*/）則比較它與輸出堆疊中棧頂的操作符，如果優先權小於或等於棧頂的操作符，那麼將棧頂的操作符彈出並加入輸出佇列（循環，直到上述條件不滿足），最後將本次的操作符壓入堆疊。
4.如果是左括號，壓入堆疊
5.如果是右括號，從棧中不斷的彈出運算符，並加入輸出佇列，知道棧頂的元素為左括號。彈出左括號，不加入輸出佇列。如果沒有發現左括號，表示原來的表達式中括號不對稱，有誤差。
6.若輸入佇列為空，而棧中尚有運算元時，若棧頂的運算子為左括號，表示原運算式有不符的括號。將堆疊中的操作符逐一彈出，加入輸出佇列。
7.完成

三、轉換程式碼實作

function isOperator(value){
	var operatorString = "+-*/()";
	return operatorString.indexOf(value) > -1
}

function getPrioraty(value){
	switch(value){
		case '+':
		case '-':
			return 1;
		case '*':
		case '/':
			return 2;
		default:
			return 0;
	}
}

function prioraty(o1, o2){
	return getPrioraty(o1) <= getPrioraty(o2);
}

function dal2Rpn(exp){
	var inputStack = [];
	var outputStack = [];
	var outputQueue = [];

	for(var i = 0, len = exp.length; i < len; i++){
		var cur = exp[i];
		if(cur != ' ' ){
			inputStack.push(cur);
		}
	}
	console.log('step one');
	while(inputStack.length > 0){
		var cur = inputStack.shift();
		if(isOperator(cur)){
			if(cur == '('){
				outputStack.push(cur);
			}else if(cur == ')'){
				var po = outputStack.pop();
				while(po != '(' && outputStack.length > 0){
					outputQueue.push(po);
					po = outputStack.pop();
				}
				if(po != '('){
					throw "error: unmatched ()";
				}
			}else{
				while(prioraty(cur, outputStack[outputStack.length - 1]) && outputStack.length > 0){
					outputQueue.push(outputStack.pop());
				}
				outputStack.push(cur);
			}
		}else{
			outputQueue.push(new Number(cur));
		}
	}
	console.log('step two');
	if(outputStack.length > 0){
		if(outputStack[outputStack.length - 1] == ')' || outputStack[outputStack.length - 1] == '('){
			throw "error: unmatched ()";
		}
		while(outputStack.length > 0){
			outputQueue.push(outputStack.pop());
		}
	}
	console.log('step three');
	return outputQueue;

}

console.log(dal2Rpn('1 + 2'));
console.log(dal2Rpn('1 + 2 + 3'));
console.log(dal2Rpn('1 + 2 * 3'));
console.log(dal2Rpn('1 + 2 * 3 - 4 / 5'));
console.log(dal2Rpn('( 1 + 2 )'));

console.log(dal2Rpn('( 1 + 2 ) * ( 3 - 4 ) / 5'));
console.log(dal2Rpn('( 1 + 2 ) * (( 3 - 4 ) / 5)'));

四、逆波蘭表達式求值

1.從輸入佇列中彈出一個記號
2.如果是操作數，加入輸出堆疊
3.如果是一個操作符，從輸出堆疊中彈出兩個操作數並進行計算，並將計算得到的值壓入輸出堆疊。
4.循環操作，如果輸入佇列為空，且輸出堆疊只有一個數則這個數為結果，否則是出現了多餘的操作數。

五、計算程式碼

function evalRpn(rpnQueue){
	var outputStack = [];
	while(rpnQueue.length > 0){
		var cur = rpnQueue.shift();

		if(!isOperator(cur)){
			outputStack.push(cur);
		}else{
			if(outputStack.length < 2){
				throw "unvalid stack length";
			}
			var sec = outputStack.pop();
			var fir = outputStack.pop();

			outputStack.push(getResult(fir, sec, cur));
		}
	}

	if(outputStack.length != 1){
		throw "unvalid expression";
	}else{
		return outputStack[0];
	}
}

六、結語

逆波蘭表示法，在初次接觸的時候感覺不太習慣，但是熟悉之後，會發現，其實思路特別簡單，不像中綴表示法，還有各種優先級啊，還有小括號之類的，邏輯特別麻煩，還是逆波蘭表示法比較簡潔，完全不用考慮優先級，也沒用小括號，中括號還有大括號攪局。