遞歸方法是一種呼叫自身的方法。許多數學函數是使用遞歸定義的。讓我們從一個簡單的例子開始。數字 n 的階乘可以遞歸定義如下:
0! = 1;
嗯! = n × (n - 1)!; n> 0
如何找到給定 n 的 n!?找到 1! 很容易,因為您知道 0! 是 1,而 1! 是 1 × 0 ! 。假設你知道(n - 1)!,你可以透過使用n × (n - 1)!立即獲得n!。因此,計算 n! 的問題就簡化為計算 (n - 1)!。當計算 (n - 1)! 時,您可以遞歸地應用相同的想法,直到 n 減少到 0.
設 factorial(n) 計算 n! 的方法。如果您使用 n = 0 呼叫該方法,它會立即傳回結果。此方法知道如何解決最簡單的情況,稱為基本情況或停止條件。如果您使用 n > 呼叫該方法; 0,它將問題簡化為計算 n - 1 階乘的子問題。 子問題本質上與原始問題相同,但更簡單或更小。由於子問題與原始問題具有相同的屬性,因此您可以使用不同的參數來呼叫該方法,稱為遞歸呼叫。
計算factorial(n)的遞迴演算法可以簡單描述如下:
如果(n == 0)
回傳 1;
其他
返回 n * 階乘(n - 1);
遞歸調用可能會導致更多的遞歸調用,因為該方法不斷將子問題劃分為新的子問題。對於要終止的遞歸方法,問題最終必須減少到停止情況,此時該方法將結果傳回給其呼叫者。然後呼叫者執行計算並將結果傳回給自己的呼叫者。這個過程一直持續到結果傳回原始呼叫者為止。現在可以透過將 n 乘以階乘(n - 1) 的結果來解決原來的問題。
下面的程式碼給了一個完整的程序,提示使用者輸入一個非負整數並顯示該數字的階乘。

factorial 方法(第 17-22 行)本質上是將階乘的遞歸數學定義直接轉換為 Java 程式碼。對 factorial 的呼叫是遞歸的,因為它呼叫自身。傳遞給 factorial 的參數會遞減,直到達到 0 的基本情況。
您將了解如何撰寫遞歸方法。遞歸在幕後如何運作?下圖說明了遞歸呼叫的執行過程,從 n = 4.
開始
遞歸呼叫時棧空間的使用如下圖。
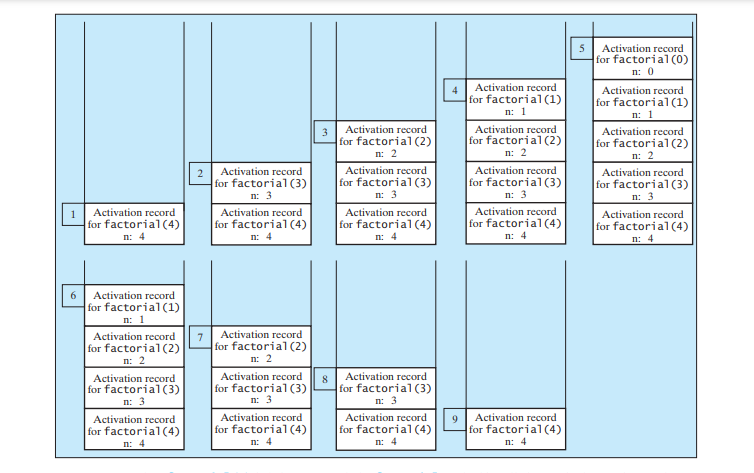
使用循環實作 factorial 方法更簡單、更有效率。然而,我們在這裡使用遞歸階乘方法來示範遞歸的概念。在本章後面,我們將介紹一些本質上是遞歸的問題,如果不使用遞迴就很難解決。
如果遞歸不能以允許問題最終收斂到基本情況的方式減少問題,或者未指定基本情況,則可能會發生無限遞歸。例如,假設您錯誤地將 factorial 方法寫如下:
公用靜態長階乘(int n) {
返回 n * 階乘(n - 1);
}
此方法無限運行並導致 StackOverflowError.
本節討論的範例顯示了一個呼叫自身的遞歸方法。這稱為直接遞歸。也可以建立間接遞歸。當方法 A 呼叫方法 B 時,會發生這種情況,方法 B 又呼叫方法 A。遞歸中甚至可以涉及更多方法。例如,方法A 呼叫方法B,方法B 呼叫方法
C,方法C 呼叫方法A。以上是案例研究:計算階乘的詳細內容。更多資訊請關注PHP中文網其他相關文章!




