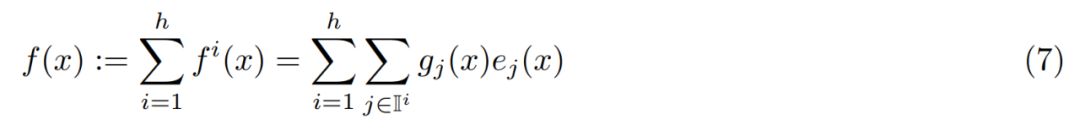釋放進一步擴展 Transformer 的潛力,同時還可以保持運算效率。
標準 Transformer 架構中的前饋(FFW)層會隨著隱藏層寬度的增加而導致計算成本和激活內存的線性增加。在大語言模型(LLM)體量不斷增大的現在,稀疏混合專家(MoE)架構已成為解決此問題的可行方法,它將模型大小與計算成本分開。許多新興的 MoE 模型都可以實現相同體積之上,更好的性能與更強大的表現。 最近發現的細粒度 MoE 擴展定律表明,更高的粒度可帶來更好的性能。然而由於計算和優化方面的挑戰,現有的 MoE 模型僅限於低數量專家。 本週二,Google DeepMind 的新研究引入了一種參數高效的專家檢索機制,其利用乘積密鑰技術從一百萬個微型專家中進行稀疏檢索。 
連結:https://arxiv.org/abs/2407.04153該方法嘗試透過用於路由的學習索引結構有效地串聯到大量微小專家,從而將計算成本與參數計數分離。與密集的 FFW、粗粒度 MoE 和產品金鑰記憶體 (PKM) 層相比,表現出卓越的效率。 這項工作引入了參數高效專家檢索(PEER) 架構(parameter efficient expert retrieval),利用產品金鑰(product key)檢索高效地路由到大量專家,將計算成本與參數量分離。這種設計在實驗中展示了卓越的運算效能水平,將其定位為擴展基礎模型的密集 FFW 層的競爭性替代方案。這項工作的主要貢獻是:極端 MoE 設定的探索:與先前的 MoE 研究中對少數大型專家的關注不同,這項工作研究了眾多小型專家的未充分探索的情況。 用於路由的學習索引結構:首次證明學習索引結構可以有效地路由到超過一百萬個專家。 新的層設計:將產品金鑰路由與單一神經元專家結合,我們引入了 PEER 層,它可以擴展層容量而無需大量計算開銷。實證結果表明,與密集 FFW、粗粒度 MoE 和產品金鑰記憶體 (PKM) 層相比,其效率更高。 綜合消融研究:我們研究了 PEER 的不同設計選擇(例如專家數量、活動參數、頭數量和查詢批量規範化)對語言建模任務的影響。 本節中,研究者詳解了參數高效專家檢索(PEER) 層,它一種混合專家架構,使用路由中的產品和單神經元MLP作為專家。下圖 2 展示了 PEER 層內的計算過程。 
PEER 層概覽。從形式上看,PEER 層是一個函數f : R^n → R^m,它由三個部分組成:一個由N 個專家組成的池E := {e_i}^N_i=1,其中每個專家e_i : R^n → R^m 與f 共用相同的簽章;一組對應的N 個產品金鑰K := {k_i}^N_i=1 ⊂ R^d ;以及一個查詢網路q : R^n → R ^d,它將輸入向量x ∈ R^n 對應到查詢向量q (x)。 令 T_k 表示 top-k 運算子。給定輸入 x,首先檢索 k 個專家的子集,這些專家對應的產品鍵與查詢 q (x) 具有最高的內積。 
然後將非線性激活(例如 softmax 或 sigmoid)應用於前 k 個專家的查詢鍵內積,以獲得路由分數。 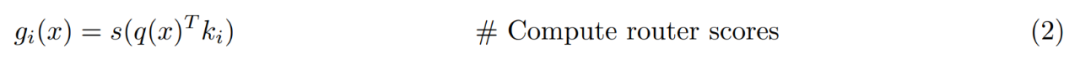
最後透過對路由分數加權的專家輸出進行線性組合來計算輸出。 
產品金鑰檢索。由於研究者打算使用大量專家(N ≥ 10^6),單純計算公式 1 中的前 k 個索引可能成本非常高,因此應用了產品金鑰檢索技術。他們不使用N 個獨立的d 維向量作為密鑰k_i,而是透過連接兩個獨立的d/2 維子密鑰集(即C, C ′ ⊂ R d/2) 中的向量來創建它們: 
參數高效專家和多頭檢索。與其他 MoE 架構不同,這些架構通常會將每個專家的隱藏層設定為與其他 FFW 層相同的大小。而在PEER 中,每個專家e_i 都是一個單例MLP,換句話說,它只有一個帶有單一神經元的隱藏層:
研究者沒有改變單一專家的規模,而是使用了多頭檢索來調整PEER 層的表達能力,這類似於transformer 中的多頭注意力機制和PKM 中的多頭記憶。 具體來說,他們使用 h 個獨立的查詢網絡,每個網絡計算自己的查詢並檢索一組單獨的 k 個專家。不過,不同的頭共享同一個專家池,具有相同的產品金鑰集。這 h 個頭的輸出簡單地總結如下: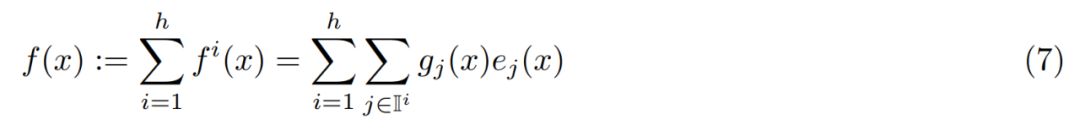
為什麼要有大量的小專家?給定的 MoE 層可以用三個超參數來表徵它:參數總數 P、每個 token 的活躍參數數量 P_active 和單一專家的大小 P_expert。 Krajewski 等人(2024) 表明,MoE 模型的scaling law 具有以下形式:
對於PEER,研究者透過設定d_expert = 1 來使用盡可能最小的專家規模,激活神經元的數量是檢索頭的數量乘以每個頭檢索到的專家數量:d_active = hk。因此,PEER 的粒徑始終為 G = P_active/P_expert = d_active/d_expert = hk。 
在根據isoFLOP 曲線確定每種方法的計算最優模型後,研究者在以下幾個流行語言建模資料集上評估了這些預訓練模型的性能:
- 研究者根據訓練期間使用的 FLOP 預算對模型進行了分組。可以看到,PEER 在這些語言建模資料集上的困惑度最低。
在消融實驗中,研究者改變了專家總數。下圖 1 中 isoFLOP 曲線所示的模型都有超過一百萬個(1024^2 )專家。
研究者選擇了isoFLOP 最優位置的模型,並改變了PEER 層中的專家數量(N = 128^2、256^2、512^2、1024^2),同時保持活躍專家數量不變(h = 8,k = 16)。結果如下圖 3 (a) 所示。 可以看到,isoFLOP 曲線在具有 1024^2 個專家的 PEER 模型和相應的密集主幹之間進行插值,而無需用 PEER 層替換中間塊中的 FFW 層。這表明,只需增加專家數量即可提高模型效能。 同時,研究者改變了活躍專家的數量。他們系統性地改變了活躍專家的數量(hk = 32、64、128、256、512),同時保持專家總數不變(N = 1024^2)。對於給定的 hk,研究者則聯合改變 h 和 k 以確定最佳組合。下圖 3 (b) 繪製了關於頭數量 (h) 的 isoFLOP 曲線。 
下表 2 列出了使用和不使用 BN 時不同數量專家的專家使用率和不均勻性。可以看到,即使對於 1M 個專家,專家使用率也接近 100%,使用 BN 可以使專家的利用率更加均衡,困惑度更低。這些發現證明了 PEER 模型在利用大量專家方面的有效性。 
研究者也比較了有無 BN 的 isoFLOP 曲線。下圖 4 顯示,有 BN 的 PEER 模型通常可以達到較低的困惑度。雖然差異並不顯著,但在 isoFLOP 最適區域附近差異最為明顯。 
PEER 研究只有一位作者 Xu He(Owen),他是 Google DeepMind 研究科學家,2017 年博士畢業於荷蘭格羅寧根大學。 
以上是單一作者論文,Google提出百萬專家Mixture,超越密集前饋、稀疏MoE的詳細內容。更多資訊請關注PHP中文網其他相關文章!