TPAMI 2024 | ProCo: 無限contrastive pairs的長尾對比學習

AIxiv專欄是本站發布學術、技術內容的欄位。過去數年，本站AIxiv專欄接收通報了2,000多篇內容，涵蓋全球各大專院校與企業的頂尖實驗室，有效促進了學術交流與傳播。如果您有優秀的工作想要分享，歡迎投稿或聯絡報道。投稿信箱：liyazhou@jiqizhixin.com；zhaoyunfeng@jiqizhixin.com

本論文第一作者杜超群是清華大學自動化系 2020 級直博生。導師為黃高副教授。此前於清華大學物理系獲理學士學位。研究興趣為不同資料分佈上的模型泛化和穩健性研究，如長尾學習，半監督學習，遷移學習等。在 TPAMI、ICML 等國際級期刊、會議上發表多篇論文。

個人主頁：https://andy-du20.github.io

本文介紹清華大學的一篇關於長尾視覺識別的論文: Probabilistic Contrastive Learning for Long-Tailed Visual Recognition. TPAMI 2024 錄用，程式碼已開源。

研究主要關注對比學習在長尾視覺識別任務中的應用，提出了一種新的長尾對比學習方法ProCo，透過對contrastive loss 的改進實現了無限數量contrastive pairs 的對比學習，有效解決了監督對比學習(supervised contrastive learning)[1] 對batch (memory bank) size 大小的固有依賴問題。除了長尾視覺分類任務，該方法還在長尾半監督學習、長尾目標偵測和平衡資料集上進行了實驗，取得了顯著的效能提升。

• 論文連結: https://arxiv.org/pdf/2403.06726

• 專案連結: https://githubo.com/LeapLabTH學習在自監督學習中的成功表明了其在學習視覺特徵表示方面的有效性。影響對比學習表現的核心因素是

  contrastive pairs 的數量
，這使得模型能夠從更多的負樣本中學習，體現在兩個最具代表性的方法SimCLR [2] 和MoCo [3] 中分別為batch size 和memory bank 的大小。然而在長尾視覺辨識任務中，由於

類別不均衡

，增加contrastive pairs 的數量所帶來的增益會產生嚴重的邊際遞減效應，這是由於大部分的contrastive pairs 都是由頭部類別的樣本構成的，

難以覆蓋到尾部類別

。 例如，在長尾Imagenet 資料集中，若batch size (memory bank) 大小設為常見的4096 和8192，那麼每個batch (memory bank) 中平均分別有212 個和89 個類別的 個類別的樣本數不足一個。 因此，ProCo 方法的核心 idea 是：在長尾數據集上，透過對每類數據的分佈進行

建模、參數估計並從中採樣

以構建 contrastive pairs，保證能夠覆蓋到所有的類別。進一步，當採樣數量趨於無窮時，可以從理論上嚴格推導出contrastive loss 期望的解析解，從而直接以此作為優化目標，避免了對contrastive pairs 的低效採樣，實現無限數量contrastive pairs 的對比學習。 然而，實現以上想法主要有以下幾個困難：

如何對每類資料的分佈進行建模。

如何有效率地估計分佈的參數，尤其是對於樣本數量較少的尾部類別。

• 如何保證 contrastive loss 的期望的解析解存在且可計算。

• 事實上，以上問題可以透過一個統一的機率模型來解決，即選擇一個簡單有效的機率分佈對特徵分佈進行建模，從而可以利用最大似然估計高效地估計分佈的參數，併計算期望contrastive loss 的解析解。

由於對比學習的特徵是分佈在單位超球面上的，因此一個可行的方案是選擇球面上的von Mises-Fisher (vMF) 分佈作為特徵的分佈（該分佈類似於球面上的正態分佈） 。 vMF 分佈參數的最大似然估計有近似解析解且僅依賴於特徵的一階矩統計量，因此可以高效地估計分佈的參數，並且嚴格推導出contrastive loss 的期望，從而實現無限數量contrastive pairs 的對比學習。

Figure 1 The ProCo algorithm estimates the distribution of samples based on the characteristics of different batches. By sampling an unlimited number of samples, the analytical solution of the expected contrastive loss can be obtained, effectively eliminating the inherent dependence of supervised contrastive learning on the batch size (memory bank) size. .

Details of the method

The following will introduce the ProCo method in detail from four aspects: distribution assumption, parameter estimation, optimization objectives and theoretical analysis.

Distribution Assumption

As mentioned before, the features in contrastive learning are constrained to the unit hypersphere. Therefore, it can be assumed that the distribution obeyed by these features is the von Mises-Fisher (vMF) distribution, and its probability density function is:

where z is the unit vector of p-dimensional features, I is the modified Bessel function of the first kind,



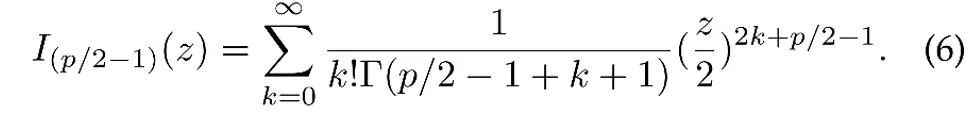
μ is the mean direction of the distribution, κ is the concentration parameter, which controls the degree of concentration of the distribution. When κ is larger, the degree of sample clustering near the mean is higher; when κ =0, the vMF distribution degenerates into a sphere. uniform distribution.

Parameter estimation

Based on the above distribution assumption, the overall distribution of data features is a mixed vMF distribution, where each category corresponds to a vMF distribution.



where the parameter represents the prior probability of each category, corresponding to the frequency of category y in the training set. The mean vector and lumping parameter of the feature distribution are estimated by maximum likelihood estimation.

Assuming that N independent unit vectors are sampled from the vMF distribution of category y, the maximum likelihood estimate (approximately) [4] of the mean direction and concentration parameters satisfies the following equation:



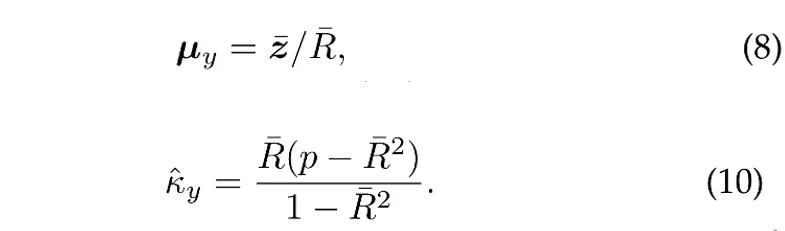
where is the sample mean, is the modulus length of the sample mean. In addition, in order to utilize historical samples, ProCo adopts an online estimation method, which can effectively estimate the parameters of the tail category.

Optimization objective

Based on the estimated parameters, a straightforward approach is to sample from the mixed vMF distribution to construct contrastive pairs. However, sampling a large number of samples from the vMF distribution in each training iteration is inefficient. Therefore, this study theoretically extends the number of samples to infinity and strictly derives the analytical solution of the expected contrast loss function directly as the optimization goal.



By introducing an additional feature branch (representation learning based on this optimization goal) during the training process, this branch can be trained together with the classification branch and will not increase since only the classification branch is needed during inference Additional computational cost. The weighted sum of the losses of the two branches is used as the final optimization goal, and α=1 is set in the experiment. Finally, the overall process of the ProCo algorithm is as follows: Theoretical analysis

In order to further analyze the To theoretically verify the effectiveness of the ProCo method, the researchers analyzed its generalization error bound and excess risk bound. To simplify the analysis, it is assumed here that there are only two categories, namely y∈{-1,+1}. The analysis shows that the generalization error bound is mainly controlled by the number of training samples and the variance of the data distribution. This finding is consistent with The theoretical analysis of related work [6][7] is consistent, ensuring that ProCo loss does not introduce additional factors and does not increase the generalization error bound, which theoretically guarantees the effectiveness of this method.

Furthermore, this method relies on certain assumptions about feature distributions and parameter estimates. To evaluate the impact of these parameters on model performance, the researchers also analyzed the excess risk bound of ProCo loss, which measures the deviation between the expected risk using estimated parameters and the Bayes optimal risk, which is in the true distribution. Expected risk under parameters.



This shows that the excess risk of ProCo loss is mainly controlled by the first-order term of the parameter estimation error.

Experimental results

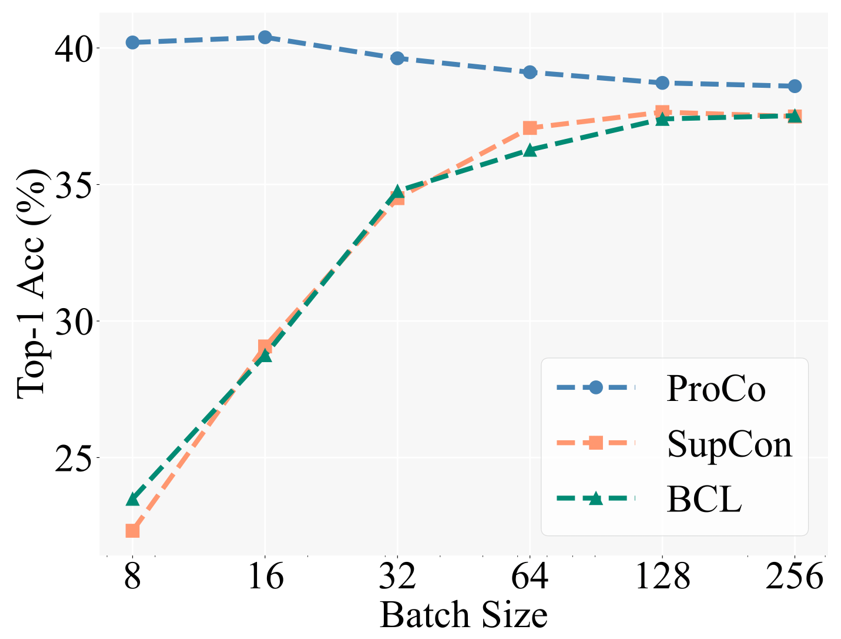
As a verification of core motivation, researchers first compared the performance of different contrastive learning methods under different batch sizes. Baseline includes Balanced Contrastive Learning [5] (BCL), an improved method also based on SCL on long-tail recognition tasks. The specific experimental setting follows the two-stage training strategy of Supervised Contrastive Learning (SCL), that is, first only use contrastive loss to train representation learning, and then train a linear classifier for testing with freeze backbone.

The figure below shows the experimental results on the CIFAR100-LT (IF100) data set. The performance of BCL and SupCon is obviously limited by the batch size, but ProCo effectively eliminates the impact of SupCon on the batch size by introducing the feature distribution of each category. dependence, thereby achieving the best performance under different batch sizes.



In addition, the researchers also conducted experiments on long-tail recognition tasks, long-tail semi-supervised learning, long-tail object detection and balanced data sets. Here we mainly show the experimental results on the large-scale long-tail data sets Imagenet-LT and iNaturalist2018. First, under a training schedule of 90 epochs, compared to similar methods of improving contrastive learning, ProCo has at least 1% performance improvement on two data sets and two backbones.



The following results further show that ProCo can also benefit from a longer training schedule. Under the 400 epochs schedule, ProCo achieved SOTA performance on the iNaturalist2018 data set, and also verified that it can compete with other non- A combination of contrastive learning methods, including distillation (NCL) and other methods. "A simple framework for contrastive learning of visual representations." International conference on machine learning. PMLR, 2020.



He, Kaiming, et al. "Momentum contrast for unsupervised visual representation learning." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2020.

1. S . Sra, “A short note on parameter approximation for von mises-fisher distributions: and a fast implementation of is (x),” Computational Statistics, 2012.

2. J. Zhu, et al. “Balanced contrastive learning for long -tailed visual recognition," in CVPR, 2022.

3. W. Jitkrittum, et al. "ELM: Embedding and logit margins for long-tail learning," arXiv preprint, 2022.

4. A. K. Menon, et al. . “Long-tail learning via logit adjustment,” in ICLR, 2021.

以上是TPAMI 2024 | ProCo: 無限contrastive pairs的長尾對比學習的詳細內容。更多資訊請關注PHP中文網其他相關文章！