投機取樣會損失大語言模型的推理精確度嗎？

Mitchell Stern 等人於 2018 年提出了投機取樣的原型概念。這個方法後來被各種工作進一步發展和完善，包括 Lookahead Decoding、REST、Medusa 和 EAGLE，投機採樣顯著加快了大型語言模型 (LLM) 的推理過程。

一個重要的問題是：LLM 中的投機取樣會損害原始模型的準確性嗎？先說答案：不會。

標準的投機採樣演算法是無損的，本文將透過數學分析和實驗來證明這一點。

數學證明

投機取樣公式可以定義如下：

其中：

• ? 是從均勻分佈中取樣的實數。
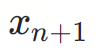• 是下一個要預測的token。
• ?(?) 是草稿模型給出的下一個token分佈。
• ?(?) 是基礎模型給出的下一個token分佈。

為簡單起見，我們省略了機率條件。實際上，? 和 ? 是基於前綴token序列 的條件分佈。

以下是 DeepMind 論文中關於這個公式無損性的證明：

如果你覺得閱讀數學方程式太枯燥，接下來我們將透過一些直觀的圖表來說明證明過程。

這是草稿模型 ? 和基礎模型 ? 的分佈示意圖：

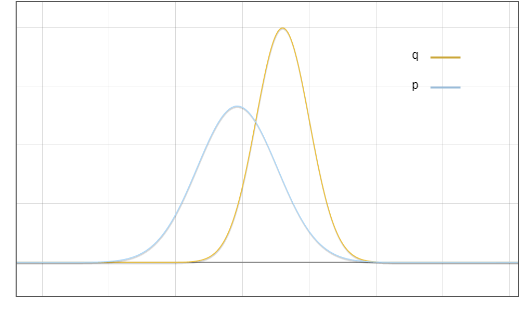
圖1：草案模型p和基礎模型q輸出分佈的機率密度函數

需要說明的是，這只是一個理想化的圖表。在實踐中，我們計算的是一個離散分佈，它看起來像這樣：

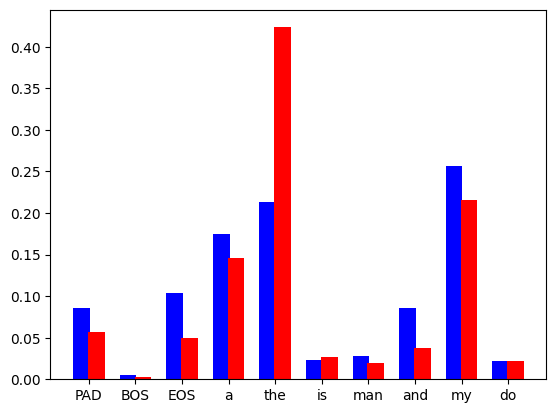
圖2：語言模型預測詞彙集中每個token的離散機率分佈，藍色條來自草稿模型，紅色條來自基礎模型。

然而，為了簡單和清晰起見，我們使用它的連續近似來討論這個問題。

現在的問題是：我們從分佈 ? 中取樣，但我們希望最終結果就像我們從 ? 中取樣。一個關鍵思想是：將紅色區域的概率搬運到黃色區域：

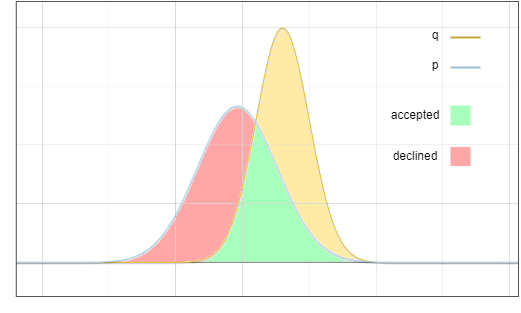
圖3：接受和拒絕採樣的區域

目標分佈 ? 可以看作是兩部分的總和：

I. 校驗接受

該分支中有兩個獨立事件：

1. 在草稿分佈 ? 上取樣產生特定token ?。機率為 ?(?)
2. 隨機變數 ? 接受該token ?。機率為：

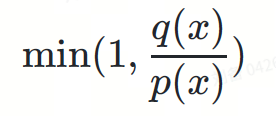
將這些機率相乘：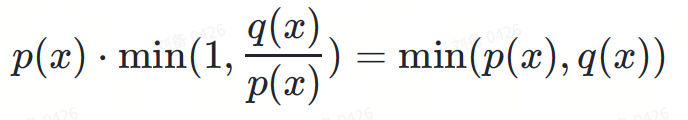

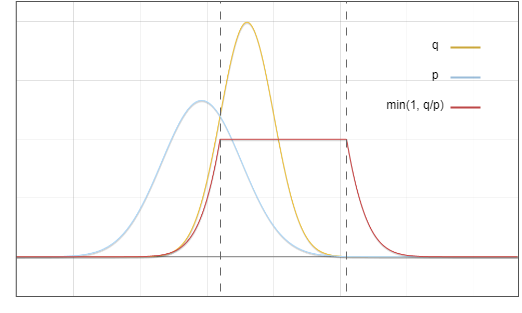
圖4：將藍線和紅線相乘，結果是圖6中的綠線

II. 校拒絕該分支拒絕該分支也有兩個獨立事件：

? 拒絕了? 中的某個token，機率為：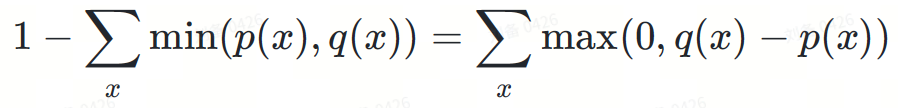 

1. 
這是一個積分值，數值與特定token x 

在分佈在分佈部分）上取樣產生特定token ?，機率為：

其分母作用是將機率分佈歸一化，以維持機率密度積分等於 1。

兩項相乘，第二項的分母被約掉：

max(0,?(?)−?(?))

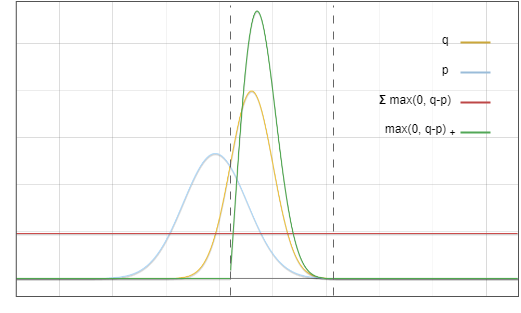
圖5. 該圖中的紅線與綠線對應函數相乘，結果等於圖6中的紅線

為什麼拒絕機率剛好可以歸一化max(0,?−?) ？看起來似乎是巧合，這裡一個重要的觀察是，圖 3 中紅色區域的面積等於黃色區域的面積，因為所有機率密度函數的積分都等於 1。

將I, II兩部分相加：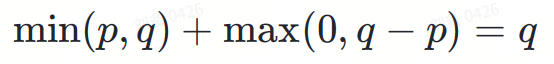 

最後，我們得到了目標分佈 ?。

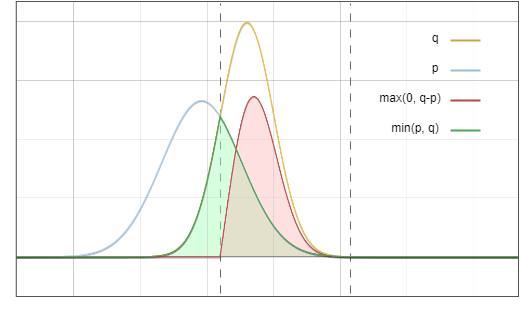
圖6. 綠色區域與紅色區域相加，剛好等於黃線以下的面積

而這正是我們的目標。

實驗

儘管我們已經從原理上證明了投機採樣是無損的，但演算法的實現仍然可能存在bug。因此，實驗驗證也是必要的。

我們對兩種情況進行了實驗：貪婪解碼的確定性方法和多項式採樣的隨機方法。

貪婪解碼

我們要求 LLM 產生兩次短篇故事，先使用普通推理，然後再使用投機取樣。兩次採樣溫度均設定為 0。我們使用了 Medusa 中的投機取樣實作。模型權重為 medusa-1.0-vicuna-7b-v1.5 及其基礎模型 vicuna-7b-v1.5。

測試運行完成後，我們得到了兩個精確相同的結果。產生的文字如下：

情況更加複雜。大多數在隨機程序中重現結果的方法都使用固定的隨機種子來利用偽隨機產生器的確定性。但是，這種方法不適合我們的場景。我們的實驗依賴大數定律：如果有足夠的樣本，則實際分佈與理論分佈之間的誤差將收斂於零。

User: Please tell a tale about a cyperpunk knight named PPIO keeps a charming llama as his pet.

advanced beyond our wildest dreams, there lived a cyberpunk knight named PPIO. PPIO was a skilled warrior, with advanced cybernetic enhancements that gave him incredible strength and spad strength and spad was gave 飾, was strength and was wasth .

One day, while out on a mission, PPIO stumbled upon a beautiful llama. Despite being a cybernetic being, PPIO had a soft spot for animals and he couldn' resister cuing int resist from ing animals and he couldn't resist表 cuing . From that day on, the llama followed PPIO wherever he went, and the two became fast friends.

The llama, whose name was Llama-ella, was a special llama. It had a unique ability to densen unique 是would let out a loud, distinctive call to alert them to the danger. PPIO was grateful for Llama-ella's ability and the two became an unstoppable team.

Together, PPIO and Llama-ellasor tookin villains to rescuing innocent people from harm. They were a force to be reckoned with, and their bravery and honor were an inspiration to all who knew them.

我們編制了四個提示文本，對LLM在每個提示下生成的首個token進行了 1,000,000 次投機採樣迭代。使用的模型權重為 

Llama3 8B Instruct 和 EAGLE-LLaMA3-Instruct-8B

。統計結果如下：

• 青: ベースモデルの出力ロジットからのソフトマックス
• 緑: ドラフトモデルの出力ロジットからのソフトマックス オレンジ: キャストマシンのサンプリングから (1,000,000 回)トークン数の割合
• の基本モデルの出力結果と標本分布の間の標準偏差は 9.694e-5 です。予想通り。

結論

投機的サンプリングは、大規模な言語モデルの推論精度を損なうことはありません。厳密な数学的分析と実践的な実験を通じて、標準的な投機的サンプリング アルゴリズムの損失のない性質を実証します。数学的証明は、投機的なサンプリング公式が基礎となるモデルの元の分布をどのように保存するかを示しています。決定論的な貪欲デコードや確率論的な多項式サンプリングを含む私たちの実験は、これらの理論的発見をさらに検証します。貪欲なデコード実験では、投機的サンプリングの有無にかかわらず同じ結果が得られましたが、多項式サンプリング実験では、多数のサンプルにわたってトークン分布の差が無視できることが示されました。

これらの結果を総合すると、投機的サンプリングによって精度を犠牲にすることなく LLM 推論が大幅に高速化され、将来的にはより効率的でアクセスしやすい AI システムへの道が開かれることが実証されています。

以上是投機取樣會損失大語言模型的推理精確度嗎？的詳細內容。更多資訊請關注PHP中文網其他相關文章！