Graph 介面定義了圖的常見操作。 Java 集合框架是設計複雜資料結構的一個很好的例子。資料結構的共同特徵在介面中定義（例如，Collection、Set、List、Queue），如下圖20.1 。抽象類別（例如，AbstractCollection、AbstractSet、AbstractList）部分實作了介面。具體類別（例如，HashSet、LinkedHashSet、TreeSet、ArrayList、LinkedList 🎜>）提供具體的實作。這種設計模式對於圖形建模很有用。我們將定義一個名為Graph 的接口，其中包含圖的所有常見操作，以及一個名為AbstractGraph 的抽象類，它部分實現Graph 接口。許多具體的圖表可以添加到設計中。例如，我們將定義名為 UnweightedGraph 和 WeightedGraph 的圖。這些介面和類別的關係如下圖所示。
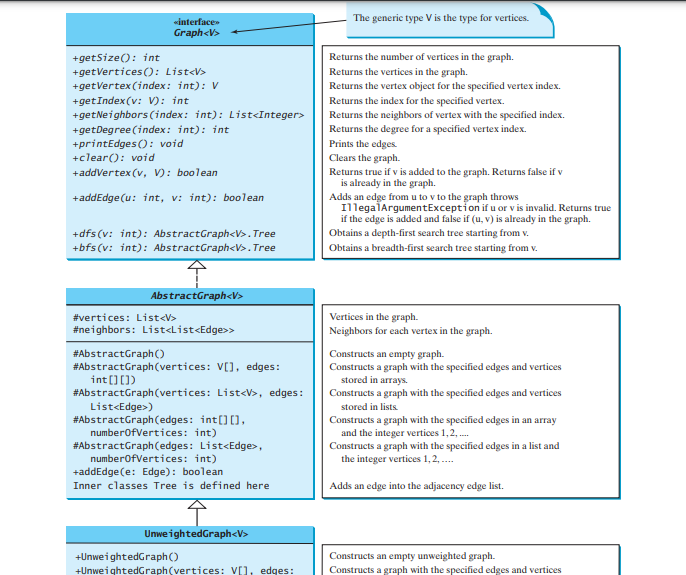
圖的常見操作有哪些？一般來說，您需要取得圖中的頂點數量，取得圖中的所有頂點，取得指定索引的頂點對象，取得指定名稱的頂點的索引，取得頂點的鄰居，取得頂點的度數，清除圖，新增頂點，新增邊，執行深度優先搜索，並執行廣度優先搜索。深度優先搜尋和廣度優先搜尋將在下一節中介紹。下圖在 UML 圖中說明了這些方法。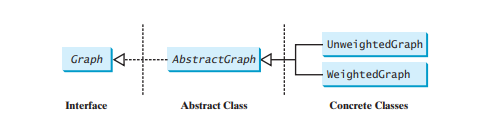 
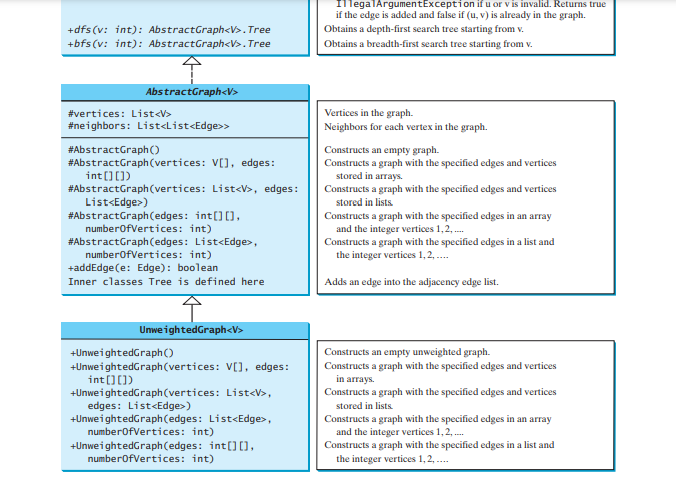AbstractGraph
AbstractGraph 類別中定義。有了這些資料字段，就足以實現 Graph 介面中定義的所有方法。為了方便起見，我們假設該圖是一個簡單圖，即一個頂點本身沒有邊，並且從頂點 u 到 v 沒有平行邊。 AbstractGraph
實現了Graph 中的所有方法，並且除了一個方便的addEdge(edge) 添加 方法之外，它沒有引入任何新方法>Edge 物件到鄰接邊列表。 UnweightedGraph 只是用五個建構子擴充 AbstractGraph，用於建立特定的 Graph 實例。 您可以建立具有任何類型頂點的圖形。每個頂點都與索引相關聯，該索引與頂點列表中該頂點的索引相同。如果您在建立圖形時未指定頂點，則頂點與其索引相同。
AbstractGraph
類別實作了Graph 介面中的所有方法。那為什麼它被定義為抽象呢？將來，您可能需要向 Graph 介面添加在 AbstractGraph 中無法實現的新方法。為了使類別易於維護，最好將 AbstractGraph 類別定義為抽象類別。
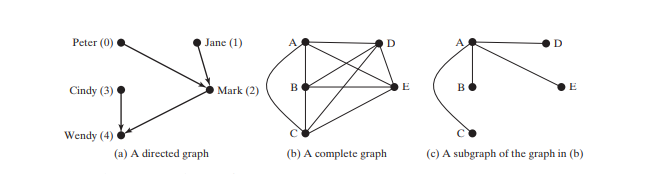
假設所有這些介面和類別都可用。下面的程式碼給出了一個測試程序，該程序創建上圖所示的圖形以及下圖 (a) 中的另一個圖形。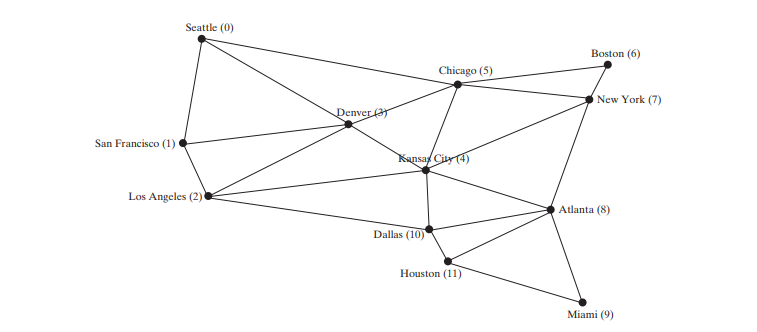 
graph1 的頂點數量：12
public class TestGraph {
public static void main(String[] args) {
String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};
// Edge array for graph
int[][] edges = {
{0, 1}, {0, 3}, {0, 5},
{1, 0}, {1, 2}, {1, 3},
{2, 1}, {2, 3}, {2, 4}, {2, 10},
{3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
{4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
{5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
{6, 5}, {6, 7},
{7, 4}, {7, 5}, {7, 6}, {7, 8},
{8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
{9, 8}, {9, 11},
{10, 2}, {10, 4}, {10, 8}, {10, 11},
{11, 8}, {11, 9}, {11, 10}
};
Graph<String> graph1 = new UnweightedGraph<>(vertices, edges);
System.out.println("The number of vertices in graph1: " + graph1.getSize());
System.out.println("The vertex with index 1 is " + graph1.getVertex(1));
System.out.println("The index for Miami is " + graph1.getIndex("Miami"));
System.out.println("The edges for graph1:");
graph1.printEdges();
// List of Edge objects for graph
String[] names = {"Peter", "Jane", "Mark", "Cindy", "Wendy"};
java.util.ArrayList<AbstractGraph.Edge> edgeList = new java.util.ArrayList<>();
edgeList.add(new AbstractGraph.Edge(0, 2));
edgeList.add(new AbstractGraph.Edge(1, 2));
edgeList.add(new AbstractGraph.Edge(2, 4));
edgeList.add(new AbstractGraph.Edge(3, 4));
// Create a graph with 5 vertices
Graph<String> graph2 = new UnweightedGraph<>(java.util.Arrays.asList(names), edgeList);
System.out.println("\nThe number of vertices in graph2: " + graph2.getSize());
System.out.println("Te edges for graph2:");
graph2.printEdges();
}
}
graph1 的邊：
西雅圖 (0): (0, 1) (0, 3) (0, 5)
舊金山 (1): (1, 0) (1, 2) (1, 3)
洛杉磯 (2): (2, 1) (2, 3) (2, 4) (2, 10)
丹佛 (3): (3, 0) (3, 1) (3, 2) (3, 4) (3, 5)
堪薩斯市 (4): (4, 2) (4, 3) (4, 5) (4, 7) (4, 8) (4, 10)
芝加哥 (5): (5, 0) (5, 3) (5, 4) (5, 6) (5, 7)
波士頓 (6): (6, 5) (6, 7)
紐約 (7): (7, 4) (7, 5) (7, 6) (7, 8)
亞特蘭大 (8): (8, 4) (8, 7) (8, 9) (8, 10) (8, 11)
邁阿密 (9): (9, 8) (9, 11)
達拉斯 (10): (10, 2) (10, 4) (10, 8) (10, 11)
休斯頓 (11): (11, 8) (11, 9) (11, 10)
The number of vertices in graph2: 5
The edges for graph2:
Peter (0): (0, 2)
Jane (1): (1, 2)
Mark (2): (2, 4)
Cindy (3): (3, 4)
Wendy (4):
The program creates graph1 for the graph in Figure 28.1 in lines 3–23. The vertices for graph1 are defined in lines 3–5. The edges for graph1 are defined in 8–21. The edges are represented using a two-dimensional array. For each row i in the array, edges[i][0] and edges[i][1] indicate that there is an edge from vertex edges[i][0] to vertex edges[i][1]. For example, the first row, {0, 1}, represents the edge from vertex 0 (edges[0][0]) to vertex 1 (edges[0][1]). The row {0, 5} represents the edge from vertex 0 (edges[2][0]) to vertex 5 (edges[2][1]). The graph is created in line 23. Line 31 invokes the printEdges() method on graph1 to display all edges in graph1.
The program creates graph2 for the graph in Figure 28.3a in lines 34–43. The edges for graph2 are defined in lines 37–40. graph2 is created using a list of Edge objects in line 43. Line 47 invokes the printEdges() method on graph2 to display all edges in graph2.
Note that both graph1 and graph2 contain the vertices of strings. The vertices are associated with indices 0, 1, . . . , n-1. The index is the location of the vertex in vertices. For example, the index of vertex Miami is 9.
Now we turn our attention to implementing the interface and classes. The codes below give the Graph interface, the AbstractGraph class, and the UnweightedGraph class, respectively.
public interface Graph<V> {
/** Return the number of vertices in the graph */
public int getSize();
/** Return the vertices in the graph */
public java.util.List<V> getVertices();
/** Return the object for the specified vertex index */
public V getVertex(int index);
/** Return the index for the specified vertex object */
public int getIndex(V v);
/** Return the neighbors of vertex with the specified index */
public java.util.List<Integer> getNeighbors(int index);
/** Return the degree for a specified vertex */
public int getDegree(int v);
/** Print the edges */
public void printEdges();
/** Clear the graph */
public void clear();
/** Add a vertex to the graph */
public void addVertex(V vertex);
/** Add an edge to the graph */
public void addEdge(int u, int v);
/** Obtain a depth-first search tree starting from v */
public AbstractGraph<V>.Tree dfs(int v);
/** Obtain a breadth-first search tree starting from v */
public AbstractGraph<V>.Tree bfs(int v);
}
import java.util.*;
public abstract class AbstractGraph<V> implements Graph<V> {
protected List<V> vertices = new ArrayList<>(); // Store vertices
protected List<List<Edge>> neighbors = new ArrayList<>(); // Adjacency lists
/** Construct an empty graph */
protected AbstractGraph() {}
/** Construct a graph from vertices and edges stored in arrays */
protected AbstractGraph(V[] vertices, int[][] edges) {
for(int i = 0; i < vertices.length; i++)
addVertex(vertices[i]);
createAdjacencyLists(edges, vertices.length);
}
/** Construct a graph from vertices and edges stored in List */
protected AbstractGraph(List<V> vertices, List<Edge> edges) {
for(int i = 0; i < vertices.size(); i++)
addVertex(vertices.get(i));
createAdjacencyLists(edges, vertices.size());
}
/** Construct a graph for integer vertices 0, 1, 2 and edge list */
protected AbstractGraph(List<Edge> edges, int numberOfVertices) {
for(int i = 0; i < numberOfVertices; i++)
addVertex((V)(new Integer(i))); // vertices is {0, 1, ...}
createAdjacencyLists(edges, numberOfVertices);
}
/** Construct a graph from integer vertices 0, 1, and edge array */
protected AbstractGraph(int[][] edges, int numberOfVertices) {
for(int i = 0; i < numberOfVertices; i++)
addVertex((V)(new Integer(i))); // vertices is {0, 1, ...}
createAdjacencyLists(edges, numberOfVertices);
}
/** Create adjacency lists for each vertex */
private void createAdjacencyLists(int[][] edges, int numberOfVertices) {
for(int i = 0; i < edges.length; i++) {
addEdge(edges[i][0], edges[i][1]);
}
}
/** Create adjacency lists for each vertex */
private void createAdjacencyLists(List<Edge> edges, int numberOfVertices) {
for(Edge edge: edges) {
addEdge(edge.u, edge.v);
}
}
@Override /** Return the number of vertices in the graph */
public int getSize() {
return vertices.size();
}
@Override /** Return the vertices in the graph */
public List<V> getVertices() {
return vertices;
}
@Override /** Return the object for the specified vertex */
public V getVertex(int index) {
return vertices.get(index);
}
@Override /** Return the index for the specified vertex object */
public int getIndex(V v) {
return vertices.indexOf(v);
}
@Override /** Return the neighbors of the specified vertex */
public List<Integer> getNeighbors(int index) {
List<Integer> result = new ArrayList<>();
for(Edge e: neighbors.get(index))
result.add(e.v);
return result;
}
@Override /** Return the degree for a specified vertex */
public int getDegree(int v) {
return neighbors.get(v).size();
}
@Override /** Print the edges */
public void printEdges() {
for(int u = 0; u < neighbors.size(); u++) {
System.out.print(getVertex(u) + " (" + u + "): ");
for(Edge e: neighbors.get(u)) {
System.out.print("(" + getVertex(e.u) + ", " + getVertex(e.v) + ") ");
}
System.out.println();
}
}
@Override /** Clear the graph */
public void clear() {
vertices.clear();
neighbors.clear();
}
@Override /** Add a vertex to the graph */
public void addVertex(V vertex) {
if(!vertices.contains(vertex)) {
vertices.add(vertex);
neighbors.add(new ArrayList<Edge>());
}
}
/** Add an edge to the graph */
protected boolean addEdge(Edge e) {
if(e.u < 0 || e.u > getSize() - 1)
throw new IllegalArgumentException("No such index: " + e.u);
if(e.v < 0 || e.v > getSize() - 1)
throw new IllegalArgumentException("No such index: " + e.v);
if(!neighbors.get(e.u).contains(e)) {
neighbors.get(e.u).add(e);
return true;
}
else {
return false;
}
}
@Override /** Add an edge to the graph */
public void addEdge(int u, int v) {
addEdge(new Edge(u, v));
}
/** Edge inner class inside the AbstractGraph class */
public static class Edge {
public int u; // Starting vertex of the edge
public int v; // Ending vertex of the edge
/** Construct an edge for (u, v) */
public Edge(int u, int v) {
this.u = u;
this.v = v;
}
public boolean equals(Object o) {
return u == ((Edge)o).u && v == ((Edge)o).v;
}
}
@Override /** Obtain a DFS tree starting from vertex v */
public Tree dfs(int v) {
List<Integer> searchOrder = new ArrayList<>();
int[] parent = new int[vertices.size()];
for(int i = 0; i < parent.length; i++)
parent[i] = -1; // Initialize parent[i] to -1
// Mark visited vertices
boolean[] isVisited = new boolean[vertices.size()];
// Recursively search
dfs(v, parent, searchOrder, isVisited);
// Return a search tree
return new Tree(v, parent, searchOrder);
}
/** Recursive method for DFS search */
private void dfs(int u, int[] parent, List<Integer> searchOrder, boolean[] isVisited) {
// Store the visited vertex
searchOrder.add(u);
isVisited[u] = true; // Vertex v visited
for(Edge e: neighbors.get(u)) {
if(!isVisited[e.v]) {
parent[e.v] = u; // The parent of vertex e.v is u
dfs(e.v, parent, searchOrder, isVisited); // Recursive search
}
}
}
@Override /** Starting bfs search from vertex v */
public Tree bfs(int v) {
List<Integer> searchOrder = new ArrayList<>();
int[] parent = new int[vertices.size()];
for(int i = 0; i < parent.length; i++)
parent[i] = -1; // Initialize parent[i] to -1
java.util.LinkedList<Integer> queue = new java.util.LinkedList<>(); // list used as queue
boolean[] isVisited = new boolean[vertices.size()];
queue.offer(v); // Enqueue v
isVisited[v] = true; // Mark it visited
while(!queue.isEmpty()) {
int u = queue.poll(); // Dequeue to u
searchOrder.add(u); // u searched
for(Edge e: neighbors.get(u)) {
if(!isVisited[e.v]) {
queue.offer(e.v); // Enqueue w
parent[e.v] = u; // The parent of w is u
isVisited[e.v] = true; // Mark it visited
}
}
}
return new Tree(v, parent, searchOrder);
}
/** Tree inner class inside the AbstractGraph class */
public class Tree {
private int root; // The root of the tree
private int[] parent; // Store the parent of each vertex
private List<Integer> searchOrder; // Store the search order
/** Construct a tree with root, parent, and searchOrder */
public Tree(int root, int[] parent, List<Integer> searchOrder) {
this.root = root;
this.parent = parent;
this.searchOrder = searchOrder;
}
/** Return the root of the tree */
public int getRoot() {
return root;
}
/** Return the parent of vertex v */
public int getParent(int v) {
return parent[v];
}
/** Return an array representing search order */
public List<Integer> getSearchOrder() {
return searchOrder;
}
/** Return number of vertices found */
public int getNumberOfVerticesFound() {
return searchOrder.size();
}
/** Return the path of vertices from a vertex to the root */
public List<V> getPath(int index) {
ArrayList<V> path = new ArrayList<>();
do {
path.add(vertices.get(index));
index = parent[index];
}
while(index != -1);
return path;
}
/** Print a path from the root vertex v */
public void printPath(int index) {
List<V> path = getPath(index);
System.out.print("A path from " + vertices.get(root) + " to " + vertices.get(index) + ": ");
for(int i = path.size() - 1; i >= 0; i--)
System.out.print(path.get(i) + " ");
}
/** Print the whole tree */
public void printTree() {
System.out.println("Root is: " + vertices.get(root));
System.out.print("Edges: ");
for(int i = 0; i < parent.length; i++) {
if(parent[i] != -1) {
// Display an edge
System.out.print("(" + vertices.get(parent[i]) + "' " + vertices.get(i) + ") ");
}
}
System.out.println();
}
}
}
import java.util.*;
public class UnweightedGraph<V> extends AbstractGraph<V> {
/** Construct an empty graph */
public UnweightedGraph() {}
/** Construct a graph from vertices and edges stored in arrays */
public UnweightedGraph(V[] vertices, int[][] edges) {
super(vertices, edges);
}
/** Construct a graph from vertices and edges stored in List */
public UnweightedGraph(List<V> vertices, List<Edge> edges) {
super(vertices, edges);
}
/** Construct a graph for integer vertices 0, 1, 2, and edge list */
public UnweightedGraph(List<Edge> edges, int numberOfVertices) {
super(edges, numberOfVertices);
}
/** Construct a graph from integer vertices 0, 1, and edge array */
public UnweightedGraph(int[][] edges, int numberOfVertices) {
super(edges, numberOfVertices);
}
}
The code in the Graph interface and the UnweightedGraph class are straightforward. Let us digest the code in the AbstractGraph class.
The AbstractGraph class defines the data field vertices (line 4) to store vertices and neighbors (line 5) to store edges in adjacency lists. neighbors.get(i) stores all edges adjacent to vertex i. Four overloaded constructors are defined in lines 9–42 to create a default graph, or a graph from arrays or lists of edges and vertices. The createAdjacencyLists(int[][] edges, int numberOfVertices) method creates adjacency lists from edges in an array (lines 45–50). The createAdjacencyLists(List edges, int numberOfVertices) method creates adjacency lists from edges in a list (lines 53–58).
The getNeighbors(u) method (lines 81–87) returns a list of vertices adjacent to vertex u. The clear() method (lines 106–110) removes all vertices and edges from the graph. The addVertex(u) method (lines 112–122) adds a new vertex to vertices and returns true. It returns false if the vertex is already in the graph (line 120).
The addEdge(e) method (lines 124–139) adds a new edge the adjacency edge list and returns true. It returns false if the edge is already in the graph. This method may throw IllegalArgumentException if the edge is invalid (lines 126–130).
The printEdges() method (lines 95–104) displays all vertices and edges adjacent to each vertex.
The code in lines 164–293 gives the methods for finding a depth-first search tree and a breadth-first search tree, which will be introduced in Depth-First Search (DFS) and Breadth-First Search (BFS), respectively.
以上是建模圖的詳細內容。更多資訊請關注PHP中文網其他相關文章！
