用光訓練神經網絡,清華成果最新登上了 Nature!
無法應用反向傳播演算法怎麼辦?
他們提出了一種全前向模式(Fully Forward Mode,FFM)的訓練方法,在物理光學系統中直接執行訓練過程,克服了傳統基於數位電腦模擬的限制。

簡單點說,以前需要對物理系統進行詳細建模,然後在電腦上模擬這些模型來訓練網路。而 FFM 方法省去了建模過程,讓系統直接使用實驗數據進行學習和最佳化。
這也意味著,訓練不需要再從後向前檢查每一層(反向傳播),而是可以直接從前向後更新網路的參數。
打個比方,就像拼圖一樣,反向傳播需要先看到最終圖片(輸出),然後逆向一塊塊檢查復原;而FFM 方法更像手中已有部分完成的拼圖,只需按照一些光原理(對稱互易性)繼續填充,而無需回頭檢查之前的拼圖。

這樣下來,使用FFM優勢也很明顯:
一是減少了對數學模型的依賴,可以避免模型不準確帶來的問題;二是節省了時間(同時能耗更低),使用光學系統可以並行處理大量的資料和操作,消除反向傳播也減少了整個網路中需要檢查和調整的步驟。
論文共同一作是來自清華的薛智威、週天貺,通訊作者是清華的方璐教授、戴瓊海院士。此外,清華電子系徐智昊、之江實驗室虞紹良也參與了這項研究。
消除反向傳播
一句話概括 FFM 原理:
將光學系統映射為參數化的現場神經網絡,透過測量輸出光場來計算梯度,並使用梯度下降演算法更新參數。
簡單說就是讓光學系統自學,透過觀察自己如何處理光線(即測量輸出光場)來了解自己的表現,然後利用這些資訊來逐步調整自己的設定(參數)。
下圖展示了 FFM 在光學系統中的運作機制:
其中 a 為傳統設計方法的限制;b 為光學系統的組成;c 為光學系統到神經網路的映射。

展開來說,一般的光學系統(b),包括自由空間透鏡光學和集成光子學,由調製區域(暗綠色)和傳播區域(淺綠色)組成。在這些區域中,調製區域的折射率是可調的,而傳播區域的折射率是固定的。
而這裡的調製和傳播區域可以映射到神經網路中的權重和神經元連接。
在神經網路中,這些可調整的部分就像是神經元之間的連接點,可以改變它們的強度(權重)來學習。
利用空間對稱互易性原理,數據和誤差計算可以共享相同的前向物理傳播過程和測量方法。
這有點像鏡子裡的反射,系統中的每個部分都能以相同的方式回應光的傳播和錯誤回饋。這意味著無論光如何進入系統,系統都能以一致的方式處理它,並根據結果來調整自己。
這樣,可以在現場直接計算梯度,用於更新設計區域內的折射率,從而優化系統性能。
透過現場梯度下降方法,光學系統可以逐步調整其參數,直到達到最優狀態。
原文將上述全前向模式的梯度下降方法(替代反向傳播)用方程式最終表示為:
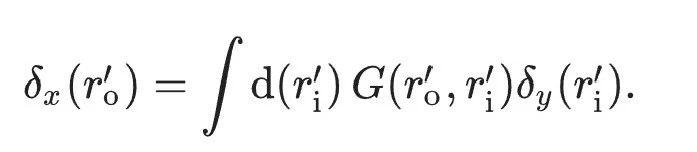
一種光學神經網路訓練方法
作為一種光學神經網路訓練的方法,FFM有以下優點:
與理想模型相當的準確率
使用FFM 可以在自由空間光學神經網路(Optical Neural Network,ONN)上實現有效的自訓練過程。

要說明這個結論,研究人員首先用一個單層的ONN 在基準資料集上進行了物件分類訓練(a)。
具體來說,他們用了一些手寫數字的圖片(MNIST 資料集)來訓練這個系統,然後將結果進行了視覺化(b)。
結果顯示,透過 FFM 學習訓練的 ONN 在實驗光場與理論光場之間相似性極高(SSIM 超過 0.97)。
換句話說,它學習得非常好,幾乎能夠完美地複製給它的範例。
不過研究者也提醒:
由於系統存在的不完美之處,理論上計算出的光場和梯度無法完全準確地反映實際物理現象。
接下來,研究人員用更複雜的圖片(Fashion-MNIST 資料集)來訓練系統辨識不同的時尚物品。
一開始,當層數從 2 層增加到 8 層,電腦訓練網路的平均準確度幾乎只有理論準確度的一半。
而透過 FFM 學習方法,系統的網路準確度提升到 92.5%,接近理論值。
這表明了,隨著網路層數的增加,傳統方法訓練的網路效能下降,而 FFM 學習能夠維持高精度。
同時,透過將非線性活化納入 FFM 學習,可以進一步提升 ONN 的效能。在實驗中,非線性 FFM 學習能夠將分類準確率從 90.4% 提高到 93.0%。
研究進一步證明,透過批量訓練非線性 ONN,錯誤傳播過程可以簡化,並且訓練時間僅增加 1 到 1.7 倍。
高解析度的聚焦能力
FFM 在實際應用中也能實現高品質的成像,即使在複雜的散射環境中也能達到接近物理極限的解析度。
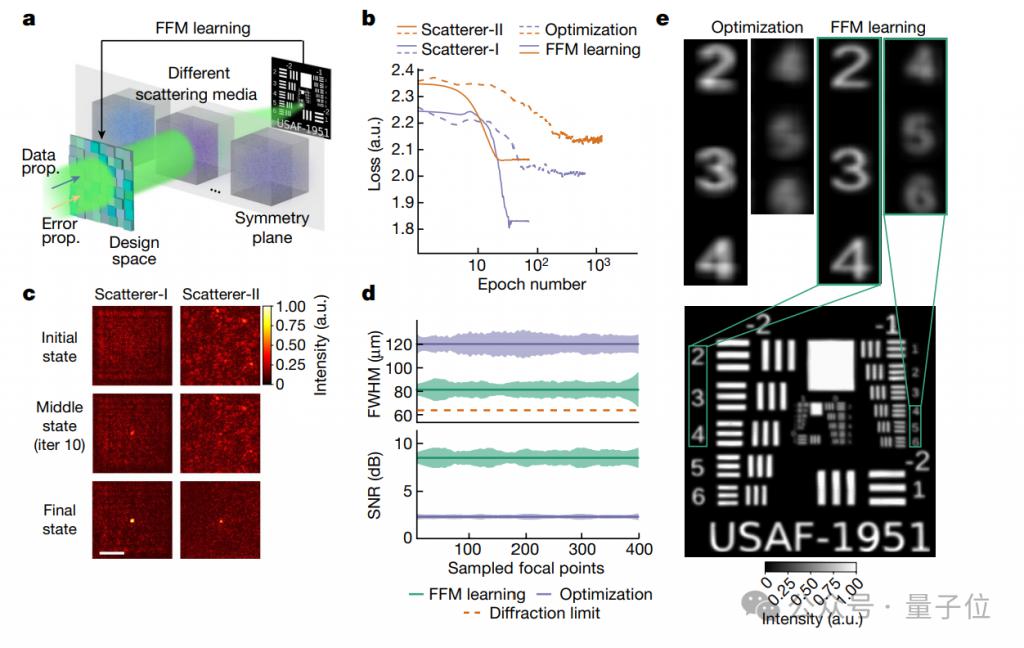
首先,當光波進入散射介質(如霧、煙或生物組織等),聚焦會變得複雜,不過光波在介質中的傳播往往保持一定的對稱性。
FFM 就利用了這種對稱性,透過優化光波的傳播路徑和相位,以減少散射效應對聚焦的負面影響。
其效果也很顯著,圖 b 展示了 FFM 與 PSO(粒子群優化)這兩種最佳化方法的對比。
具體來說,實驗採用了兩種散射介質,一種是隨機相位板(Scatterer-I),另一種是透明膠帶(Scatterer-II)。
在這兩種介質中,FFM 僅經過 25 次設計迭代就實現了收斂(更快找到最佳化解),收斂損失值分別為 1.84 和 2.07(越低效能越好)。
而 PSO 方法需要至少 400 次設計迭代才能達到收斂,且在最終收斂時的損失值為 2.01 和 2.15。
同時,圖 c 展示了 FFM 能夠不斷自我最佳化,它設計的焦點從最初的隨機分佈逐漸演化和收斂到一個緊密的焦點。
在 3.2 mm × 3.2 mm 的設計區域內,研究人員進一步對 FFM 和 PSO 優化的焦點進行了均勻採樣,並比較了它們的 FWHM(半峰全寬)和 PSNR(峰值信噪比)。
結果顯示,FFM 聚焦精度更高,成像品質更好。
圖 e 進一步評估了設計的焦點陣列在掃描位於散射介質後面的分辨率圖時的性能。
結果令人驚喜,FFM 設計的焦點尺寸接近 64.5 m 的衍射極限,這是光學成像理論上的最高解析度標準。
能夠並行成像視線之外的物體
既然在散射介質中如此厲害,研究人員又嘗試了非視距(NLOS)場景,即物體被隱藏在視線之外的地方。

FFM 利用了從隱藏物體到觀察者之間光路的空間對稱性,這允許系統透過全光學的方式在現場重建和分析動態隱藏物體。
透過設計輸入波前,FFM 能夠同時將物體中的所有網格投影到它們的目標位置,實現隱藏物體的平行恢復。
實驗中使用了字母形狀的隱藏鉻靶 "T"、"H" 和 "U",並設定了曝光時間(1 毫秒)和光功率(0.20 mW),以實現對這些動態目標的快速成像。
結果顯示,沒有 FFM 設計的波前,影像會嚴重扭曲。而 FFM 設計的波前能夠恢復所有三個字母的形狀,SSIM(結構相似性指數)達到 1.0,顯示與原始影像的高度相似性。
進一步,與人工神經網路(ANN)在光子效率和分類性能方面相比,FFM 顯著優於 ANN,尤其是在低光子條件下。
具體而言,在光子數量受限的情況下(如許多反射或高度漫射的表面),FFM 能夠自適應地糾正波前畸變,並需要更少的光子來進行準確分類。
在非 Hermitian 系統中自動搜尋異常點
FFM 方法不僅適用於自由空間光學系統,還可以擴展到整合光子系統的自我設計。

研究人員使用串聯和並聯配置的對稱光子核心,建構了一個整合神經網路(a)。
實驗中,對稱核心透過不同程度的注入電流配置了可變光衰減器(VOA),實現了不同的衰減係數,以模擬不同的權重。
図 c では、対称コアのプログラムされたマトリックス値の忠実度は非常に高く、時間ドリフトの標準偏差はそれぞれ 0.012%、0.012%、0.010% であり、マトリックス値が非常に安定していることを示しています。
そして、研究者たちは各層の誤差を視覚化しました。実験による勾配を理論上のシミュレーション値と比較すると、平均偏差は 3.5% です。
約 100 回の反復 (エポック) の後、ネットワークは収束に達します。
実験結果は、3 つの異なる対称比構成 (1.0、0.75、または 0.5) の下で、ネットワークの分類精度がそれぞれ 94.7%、89.2%、89.0% であることを示しています。
FFM手法を用いたニューラルネットワークを使用して得られた分類精度は、94.2%、89.2%、88.7%です。
対照的に、従来のコンピューター シミュレーション手法を使用してネットワークを設計した場合、実験の分類精度はそれぞれ 71.7%、65.8%、55.0% と低くなります。
最後に、研究者らは、数値シミュレーションを通じて、FFM が非エルミート システムを自己設計し、物理モデルを必要とせずに特異点の通過を達成できることも実証しました。
非エルミート系とは、エルミート条件を満たさない量子力学や光学などの分野の系を含む物理学の概念です。
エルミート特性は系の対称性とエネルギーの実数に関連しており、非エルミート系はこれらの条件を満たさない場合があります。例外点 (Exceptional Points) などの特殊な物理現象が存在します。学習行動が特定の時点で奇妙な変化を起こすシステム。
記事全文を要約すると、FFM は物理システム上に計算集約型のトレーニング プロセスを実装する方法であり、ほとんどの機械学習操作を効率的に並行して実行できます。
より詳細な実験設定とデータセット準備プロセスについては、元の記事を参照してください。
コード:
https://zenodo.org/records/10820584
「Nature」の原文:
https://www.nature.com/articles/s41586-024-07687-4
以上是清華光學 AI 登 Nature!物理神經網絡,反向傳播不需要了的詳細內容。更多資訊請關注PHP中文網其他相關文章!




