在先前的文章中,我們學習了相當多的排序演算法,例如冒泡排序、選擇排序以及插入排序。我們了解到,雖然這些排序演算法非常容易實現,但它們對於大型資料集來說效率不高,這意味著我們需要一種更有效的演算法來處理大型資料集的排序,因此需要合併排序。在本系列中,我們將介紹合併排序的工作原理以及如何在 JavaScript 中實現它。你準備好了嗎?

合併排序演算法是一種遵循分治原則的優秀排序演算法。與選擇排序和冒泡排序等更簡單的演算法不同,這些演算法多次遍歷數組來比較相鄰元素,合併排序採用了更具策略性的方法:
在處理較大的資料集時,這種方法始終優於更簡單的 O(n²) 演算法,例如選擇排序和冒泡排序。
我們已經看到合併排序是透過使用流行的分而治之方法來工作的。下面是其工作原理的直觀表示。
現在我們已經看到了它的魔力,讓我們透過使用上述方法手動排序這個陣列:[38, 27, 43, 3, 9, 82, 10]來了解合併排序演算法的工作原理。
歸併排序的第一步是將數組分成子數組,然後將每個子數組劃分為子數組,然後將子數組劃分為子數組,直到所有子數組中只剩下一項。
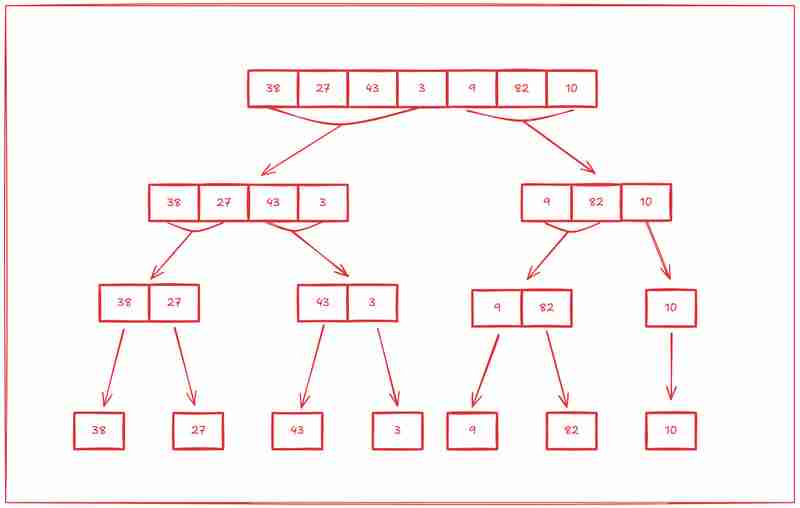
第二步是開始從頭開始對這些子陣列進行排序。
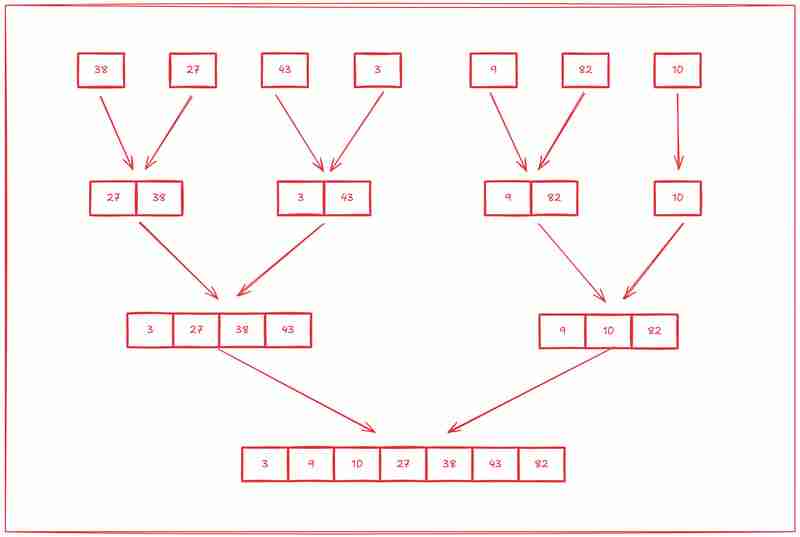
歸併排序在所有情況下(最佳、平均和最差)都實現了 O(n log n) 時間複雜度,使其比處理較大資料集的 O(n²) 演算法更有效率。
原因如下:
將此與:
進行比較對於 1,000 個元素的陣列:
歸併排序需要 O(n) 的額外空間來儲存合併期間的臨時數組。雖然這超過了冒泡排序或選擇排序所需的 O(1) 空間,但時間效率通常使得這種權衡在實踐中是值得的。
// The Merge Helper Function
function merge(left, right) {
const result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] <= right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
// Add remaining elements
while (leftIndex < left.length) {
result.push(left[leftIndex]);
leftIndex++;
}
while (rightIndex < right.length) {
result.push(right[rightIndex]);
rightIndex++;
}
return result;
}
const result = []; let leftIndex = 0; let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] <= right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
while (leftIndex < left.length) {
result.push(left[leftIndex]);
leftIndex++;
}
function mergeSort(arr) {
// Base case
if (arr.length <= 1) {
return arr;
}
// Divide
const middle = Math.floor(arr.length / 2);
const left = arr.slice(0, middle);
const right = arr.slice(middle);
// Conquer and Combine
return merge(mergeSort(left), mergeSort(right));
}
if (arr.length <= 1) {
return arr;
}
const middle = Math.floor(arr.length / 2); const left = arr.slice(0, middle); const right = arr.slice(middle);
return merge(mergeSort(left), mergeSort(right));
讓我們看看它是如何排序的 [38, 27, 43, 3]:
// The Merge Helper Function
function merge(left, right) {
const result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] <= right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
// Add remaining elements
while (leftIndex < left.length) {
result.push(left[leftIndex]);
leftIndex++;
}
while (rightIndex < right.length) {
result.push(right[rightIndex]);
rightIndex++;
}
return result;
}
const result = []; let leftIndex = 0; let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] <= right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
合併排序作為一種高效的排序演算法脫穎而出,在大型資料集上始終表現良好。雖然與更簡單的排序演算法相比,它需要額外的空間,但其 O(n log n) 時間複雜度使其成為許多效能至關重要的實際應用程式的首選。
重點:
確保您不會錯過本系列的任何部分,並與我聯繫以進行更深入的了解
關於軟體開發(Web、伺服器、行動或抓取/自動化)、資料的討論
結構和演算法,以及其他令人興奮的技術主題,請關注我:

敬請期待並祝您編碼愉快????
以上是了解合併排序演算法:掌握排序演算法的初學者指南的詳細內容。更多資訊請關注PHP中文網其他相關文章!




