想像一隻老鼠在複雜的迷宮中尋找起司。每一條路看起來都充滿希望,直到它走進死胡同。它如何能夠有系統地探索每條路線,而不遺漏任何可能的解決方案?這就是回溯演算法的用武之地,它是解決複雜謎題和現實世界問題的強大工具。
回溯是一種遞歸演算法技術,它逐步建立解決方案並放棄無法得出有效解決方案的路徑。它的意義在於它的簡單性和多功能性,使其適用於人工智慧、機器人和優化等領域。
在本部落格中,我們將深入探討回溯的工作原理,探索其實際應用,並專注於解決迷宮中的老鼠問題。
回溯是一種深度優先搜尋 (DFS) 技術,用於透過增量建立解決方案來解決問題。當路徑導致無效狀態時,演算法「回溯」到上一步並嘗試不同的選項。
老鼠走迷宮

領域:機器人
回溯在機器人技術中起著至關重要的作用,特別是在尋路和導航演算法中。自主機器人使用這種技術來探索未知環境,確保不會忽略任何潛在路線。

挑戰:穿越迷宮
機器人和搜救行動經常面臨迷宮般的環境。挑戰在於在事先不了解地形的情況下找到最佳路徑。
解
回溯演算法允許系統地探索每條可能的路線,確保找到解決方案(如果存在)。它透過回溯和探索替代路徑來處理死胡同,使其在動態場景中高度可靠。
計算複雜度:
回溯可能會在大型或複雜的迷宮中探索許多不必要的路徑,導致效率低下。
即時約束:
對於機器人等現實應用來說,速度至關重要。使用啟發式方法優化回溯(例如,對某些路徑進行優先排序)可以提高效能。
**案例研究:**自主無人機導航
一家領先的機器人公司在受災地區實施了無人機尋路回溯。無人機使用這種演算法來導航倒塌的結構,系統地探索路徑,同時避開障礙物。結果呢?更快地識別被困人員並有效分配資源。

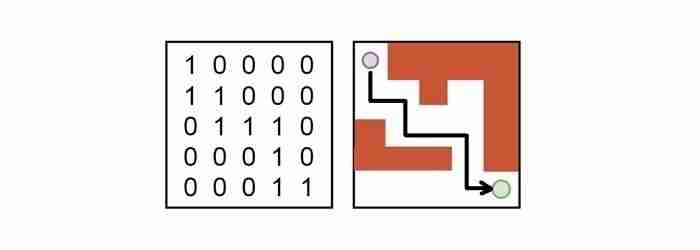
迷宮圖:老鼠運動和回溯的視覺表示。
樹形圖: 遞歸呼叫表示為決策樹。
解(0, 0)
└── 求解(1, 0)
└── 求解(1, 1)
└── 求解(2, 1)
└── 解(2, 2)
└── 解(2, 3)
└── 解(3, 3)
└── 解(4, 3)
└── 解決(4, 4)(目的地)
系統探索:確保考慮所有可能性。
簡單性:易於解決各種問題。
適應性:適用於調度、解謎和最佳化問題

回溯演算法是解決問題的基石,提供多功能性和可靠性。從幫助老鼠找到起司到引導機器人穿過迷宮,它的應用範圍廣泛且影響深遠。
隨著運算需求的成長,最佳化回溯將為新的機會打開大門,例如人工智慧系統中的即時導航和複雜決策。它的簡單和強大讓我們想起系統解決問題的美妙。
以上是尋找道路:迷宮中的老鼠的回溯演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章!




