到達角落所需清除的障礙物最少

2290。最少清除障礙物才能到達轉角

難度：難

主題：陣列、廣度優先搜尋、圖、堆疊（優先權佇列）、矩陣、最短路徑

給你一個 0 索引 大小為 m x n 的 2D 整數陣列網格。每個單元格都有兩個值之一：

• 0 代表空白單元格，
• 1 代表可以移除的障礙物。

您可以在空白儲存格之間向上、向下、向左或向右移動。

將最小個障礙物回到移除，這樣你就可以從左上角(0, 0)移到右下角角(m - 1, n - 1).

範例1：

• 輸入： grid = [[0,1,1],[1,1,0],[1,1,0]]
• 輸出： 2
• 解釋：我們可以移除 (0, 1) 和 (0, 2) 處的障礙物，創造一條從 (0, 0) 到 (2, 2) 的路徑。
  • 可以證明我們需要移除至少 2 個障礙物，因此我們返回 2。
  • 請注意，可能還有其他方法可以移除 2 個障礙物來建立一條路徑。

範例2：

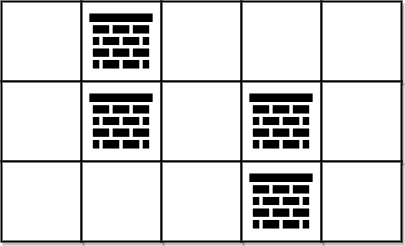
• 輸入： grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
• 輸出： 0
• 解釋：我們可以在不移除任何障礙的情況下從 (0, 0) 移動到 (2, 4)，因此我們返回 0。

約束：

• m == grid.length
• n == grid[i].length
• 1 5
• 2 5
• grid[i][j] 為 0 或 1。
• 網格[0][0] == 網格[m - 1][n - 1] == 0

提示：

1. 將網格建模為圖形，其中單元格是節點，邊是相鄰單元格之間的。有障礙物的單元格的邊緣的成本為 1，所有其他邊緣的成本為 0。
2. 你能使用0-1廣度優先搜尋或Dijkstra演算法嗎？

解：

我們需要使用圖表來模擬這個問題，其中網格中的每個單元格都是一個節點。目標是從左上角 (0, 0) 導航到右下角 (m-1, n-1)，同時最大限度地減少我們需要移除的障礙物 (1s) 的數量。

方法：

1. 圖形表示：

   • 網格中的每個單元格都是一個節點。
   • 相鄰單元格之間的移動（上、下、左、右）被視為邊緣。
   • 如果一條邊穿過帶有 1（障礙物）的單元格，則成本為 1（移除障礙物），如果它穿過 0（空單元格），則成本為 0。

2. 演算法選擇：

   • 由於我們需要最小化移除的障礙物數量，因此我們可以使用0-1 BFS（使用雙端隊列的廣度優先搜尋）或Dijkstra 演算法 以及優先級隊列。
   • 0-1 BFS 適合這裡，因為每條邊的成本為 0 或 1。

3. 0-1 BFS：

   • 我們使用deque（雙端佇列）來處理不同成本的節點：
     • 將成本為 0 的單元推到雙端隊列的前方。
     • 將成本為 1 的單元推到雙端隊列的後面。
   • 這個想法是探索網格並始終先擴展不需要移除障礙物的路徑，並且僅在必要時移除障礙物。

讓我們用 PHP 實作這個解：2290。到達角落所需清除的最小障礙物

解釋：

1. 輸入解析：

   • 網格被視為二維數組。
   • 計算行和列以進行邊界檢查。

2. 雙端隊列實作：

   • SplDoublyLinkedList用來模擬雙端佇列。支援在前面（unshift）或後面（push）添加元素。

3. 已存取陣列：

   • 追蹤已造訪過的儲存格以避免冗餘處理。

4. 0-1 BFS 邏輯：

   • 從 (0, 0) 開始，成本為 0。
   • 對於每個相鄰單元格：
     • 如果為空（grid[nx][ny] == 0），則以相同的成本將其添加到雙端隊列的前面。
     • 如果它是一個障礙物 (grid[nx][ny] == 1)，則將其添加到雙端隊列的後面，並增加成本。

5. 回傳結果：

   • 到達右下角時，回程費用。
   • 如果不存在有效路徑（儘管問題保證有一個），則回傳 -1。

---

複雜：

• 時間複雜度： O(m x n)，其中m 是行數，n 是列數。每個單元格都會被處理一次。
空間複雜度：
• O(m x n)，對於存取的陣列和雙端隊列。
此實現在給定的限制內有效地工作。

聯絡連結

如果您發現本系列有幫助，請考慮在 GitHub 上給 存儲庫 一個星號或在您最喜歡的社交網絡上分享該帖子？ 。您的支持對我來說意義重大！

如果您想要更多類似的有用內容，請隨時關注我：

• 領英
• GitHub

以上是到達角落所需清除的障礙物最少的詳細內容。更多資訊請關注PHP中文網其他相關文章！