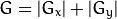前言
上一篇文章,我們講解了影像處理中的膨脹和腐蝕函數,這篇文章將做邊緣梯度計算函數。
影像的邊緣
影像的邊緣從數學上是如何表示的呢?

影像的邊緣上,鄰近的像素值應顯著地改變了。而在數學上,導數是表示改變快慢的一種方法。梯度值的大變預示著影像中內容的顯著變化了。
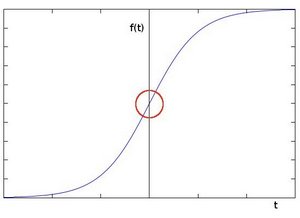
用更形象的圖像來解釋,假設我們有一張一維圖形。下圖灰階值的「躍升」表示邊緣的存在:

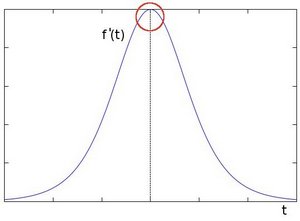
使用一階微分求導我們可以更清晰的看到邊緣「躍升」的存在(這裡顯示為高峰值):

由此我們可以得到:邊緣可以透過定位梯度值大於鄰域的相素的方法來找到。
近似梯度
例如內核為3時。
先對x方向計算近似導數:

然後對y方向計算近似導數:

然後計算梯度:

當然你也可以寫成:

函數實作
複製程式碼
複製程式碼
var Sobel = function(__src, __xorder, __yorder, __size, __borderType, __dst){
(__src && (__xorder ^ __yorder)) || error(arguments.cal. /);
if(__src.type && __src.type === "CV_GRAY"){
var kernel1,
kernel2,
height = __src.row,
width = __src. col,
dst = __dst || new Mat(height, width, CV_16I, 1),
dstData = dst.data
size = __size || 3;
>case 1:
size = 3;
case 3:
if(__xorder){
kernel = [-1, 0, 1,
-2, 0, 2,
-1, 0, 1
];
}else if(__yorder){
kernel = [-1, -2, -1,
, 0, 0,
, 2 , 1
];
}
break;
case 5:
if(__xorder){
kernel = [-1, -2, 0, 2, 1,
-4, -8, 0, 8, 4,
-6,-12, 0,12, 6,
-4, -8, 0, 8, 4,
-1, - 2, 0, 2, 1
];
}else if(__yorder){
kernel = [-1, -4, -6, -4, -1,
-2, - 8,-12, -8, -2,
, 0, 0, 0, 0,
, 8, 12, 8, 2,
, 4, 6, 4, 1
] ;
}
break;
default:
error(arguments.callee, UNSPPORT_SIZE/* {line} */);
}
FilAY216IC1ter(>} , size, height, width, kernel, dstData, __borderType);
}else{
error(arguments.callee, UNSPPORT_DATA_TYPE/* {line} */);
} dst;
};
複製程式碼 程式碼如下:
function GRAY216IC1Filter(__src, size, height, width, kernel, dstData, __borderType){
var start = size >> 1;
start, 0, 0, __borderType);
var mData = withBorderMat.data,
mWidth = withBorderMat.col;
var i, j, y, x, c;
var i, j, y, x, c;
var newValue, nowX, offsetY, offsetI;
for(i = height; i--;){
offsetI = i * width;
for(j = width; j--; ){
newValue = 0;
for(y = size; y--;){
offsetY = (y i) * mWidth;
for(x = size; x--;){
nowX = x j;
newValue = (mData[offsetY nowX] * kernel[y * size x]);
}
}
dstData[j offsetI] = new
}
dstData[j offsetI] = new
}
dstData[j offsetI] = new
}
dstData[j offsetI] = new
} } }
}
然後把內核和矩陣交給這個濾波器處理,就OK了。
複製程式碼
程式碼如下:
function convertScales(__s(__src)> || error(arguments.callee, IS_UNDEFINED_OR_NULL/* {line} */);
var height = __src.row,
width = __src.col,
channel = __src.chan. = __src.data;
if(!__dst){
if(channel === 1)
dst = new Mat(height, width, CV_GRAY);
else if(channel === 4)
dst = new Mat(height, width, CV_RGBA);
else
dst = new Mat(height, width, CV_8I, channel);
}else{
dst = __dst;
}
var dData = dst.data;
var i, j, c;
for(i = height; i--; ){
for(j = width * channel; j--;){
dData[i * width * channel j] = Math.abs(sData[i * width * channel j]);
} }
return dst;
}
複製程式碼
程式碼如下:
var addWeighted = function(__src1, betaphaalpha , __gamma, __dst){
(__src1 && __src2) || error(arguments.callee, IS_UNDEFINED_OR_NULL/* {line} */);
var height = __src1.row, widwid. ,
alpha = __alpha || 0,
beta = __beta || 0,
channel = __src1.channel,
gamma = __gamma || 0;
if(height !==__src2 .row || width !== __src2.col || channel !== __src2.channel){
error(arguments.callee, "Src2 must be the same size and channel number as src1!"/* {line} */);
return null;
}
if(!__dst){
if(__src1.type.match(/CV_d /))
dst = new Mat( height, width, __src1.depth(), channel);
else
dst = new Mat(height, width, __src1.depth());
}else{
dst =d; 🎜>}
var dData = dst.data,
s1Data = __src1.data,
s2Data = __src2.data;
var i
dData[i] = __alpha * s1Data[i] __beta * s2Data[i] gamma;
return dst;
};
這個函數很簡單,其實只是對兩個矩陣的對應元素以固定比例相加而已。
效果圖