π是一個無數人追隨的真正的神奇數字。我不是很清楚一個永遠重複的無理數的迷人之處。在我看來,我樂於計算π,也就是計算π的值。因為π是一個無理數,它是無限的。這就意味著任何對π的計算都只是個近似值。如果你計算100位,我可以計算101位並且更精確。到目前為止,有些人已經選拔出超級電腦來試圖計算最精確的π。一些極值包括 計算π的5億位。你甚至可以從網路上找到包含 π的一百億位元的文字檔案(注意啦!下載這個檔案可能得花一會兒時間,並且沒法用你平常使用的記事本應用程式打開。)。對我而言,如何用幾行簡單的Python來計算π才是我的興趣。

你總是可以 使用 math.pi 變數的 。它被 包含在 標準庫中, 在你試圖自己 計算它之前,你應該去使用它 。 事實上 , 我們將 用它來計算 精度 。作為 開始, 讓我們來看 一個 非常直截了當的 計算Pi的 方法 。像往常一樣,我將使用Python 2.7,同樣的想法和程式碼可能應用於不同的版本。我們將要使用的大部分演算法來自 Pi WikiPedia page並加以實現。讓我們看看下面的程式碼:
importsys
importmath
defmain(argv):
iflen(argv) !=1:
sys.exit('Usage: calc_pi.py <n>')
print'\nComputing Pi v.01\n'
a=1.0
b=1.0/math.sqrt(2)
t=1.0/4.0
p=1.0
foriinrange(int(sys.argv[1])):
at=(a+b)/2
bt=math.sqrt(a*b)
tt=t-p*(a-at)**2
pt=2*p
a=at;b=bt;t=tt;p=pt
my_pi=(a+b)**2/(4*t)
accuracy=100*(math.pi-my_pi)/my_pi
print"Pi is approximately: "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if__name__=="__main__":
main(sys.argv[1:])這是一個非常簡單的腳本,你可以下載,運行,修改,和隨意分享給別人。你能夠看到類似下面的輸出結果:
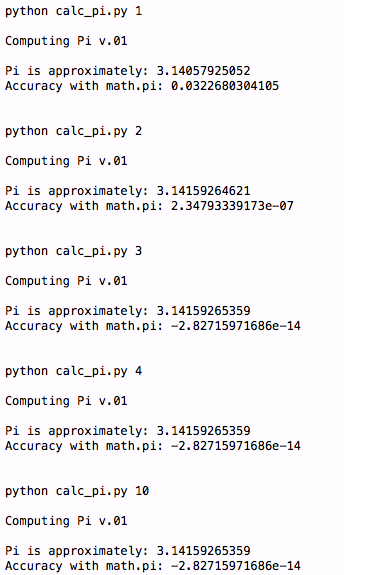
你會發現,儘管 n 大於4 ,我們逼近 Pi 精度卻沒有多大的提升。 我們可以猜到即使 n的值更大,同樣的事情(pi的逼近精度沒有提升)仍會發生。幸運的是,有不只一種方法來揭開這個謎。使用 Python Decimal (十進位)函式庫,我們可以就可以得到更精確的值來逼近Pi。讓我們來看看庫函數是如何使用的。這個簡化的版本,可以得到多於11位的數字 通常情況小Python 浮點數給出的精度。以下是Python Decimal 庫中的一個例子 :

看到這些數字。不對! 我們輸入的只是 3.14,為什麼我們得到了一些垃圾(junk)? 這是記憶體垃圾(memory junk)。 在堅果殼,Python給你想要的十進制數,再加上一點額外的值。 只要精度小於垃圾號碼開始時,它不會影響任何計算只要精度小於前面的垃圾號碼(junk number)開始時。 您可以指定你想要多少位數的通過設定getcontext().prec 。我們試試。
很好。 現在讓我們 試著用這個 來 看看我們是否能 與我們以前的 程式碼 有更好的 逼近 。 現在, 我通常 是反對 使用「 from library import * 」 , 但在這種情況下, 它會 讓程式碼 看起來更漂亮 。
importsys
importmath
fromdecimalimport*
defmain(argv):
iflen(argv) !=1:
sys.exit('Usage: calc_pi.py <n>')
print'\nComputing Pi v.01\n'
a=Decimal(1.0)
b=Decimal(1.0/math.sqrt(2))
t=Decimal(1.0)/Decimal(4.0)
p=Decimal(1.0)
foriinrange(int(sys.argv[1])):
at=Decimal((a+b)/2)
bt=Decimal(math.sqrt(a*b))
tt=Decimal(t-p*(a-at)**2)
pt=Decimal(2*p)
a=at;b=bt;t=tt;p=pt
my_pi=(a+b)**2/(4*t)
accuracy=100*(Decimal(math.pi)-my_pi)/my_pi
print"Pi is approximately: "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if__name__=="__main__":
main(sys.argv[1:])輸出結果:
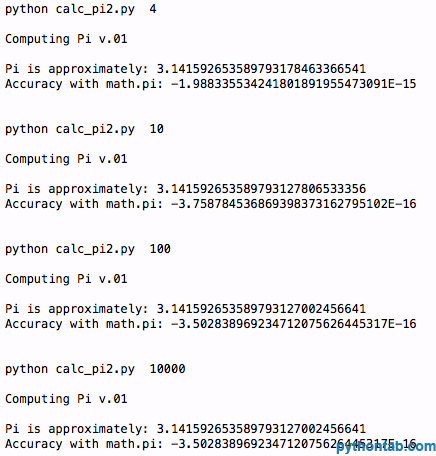
好了。我們更準確了,但看起來似乎有些捨去。從n = 100和n = 1000,我們有相同的精度。現在怎麼辦?好吧,現在我們來求助於公式。到目前為止,我們計算Pi的方式是透過對幾部分加在一起。我從DAN 的關於 Calculating Pi 的文章中發現一些程式碼。他建議我們用以下3個公式:
Bailey–Borwein–Plouffe 公式
Bellard的公式
Chudnovsky 演算法
讓我們從Bailey–Borwein–Plouffe 公式開始。它看起來是這個樣子:
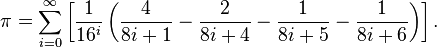
在程式碼中我們可以這樣寫它:
import sys
import math
from decimal import *
def bbp(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(1)/(16**k))*((Decimal(4)/(8*k+1))-(Decimal(2)/(8*k+4))-(Decimal(1)/(8*k+5))-(Decimal(1)/(8*k+6)))
k+=1
return pi
def main(argv):
if len(argv) !=2:
sys.exit('Usage: BaileyBorweinPlouffe.py <prec> <n>')
getcontext().prec=(int(sys.argv[1]))
my_pi=bbp(int(sys.argv[2]))
accuracy=100*(Decimal(math.pi)-my_pi)/my_pi
print"Pi is approximately "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if __name__=="__main__":
main(sys.argv[1:])拋開「 包裝」的程式碼,BBP(N)的功能是你真正想要的。你給它越大的N和給 getcontext().prec 設定越大的值,你就會讓計算越精確。讓我們來看看一些程式碼結果:
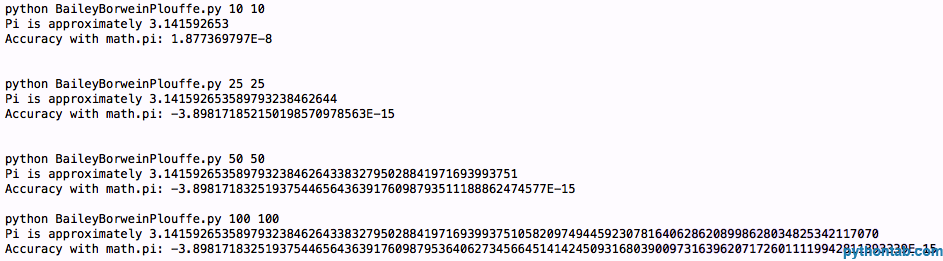
這有許多數字位。你可以看出,我們並沒有比以前更準確。所以我們需要前進到下一個公式,貝拉公式,希望能獲得更好的精確度。它看起來像這樣:
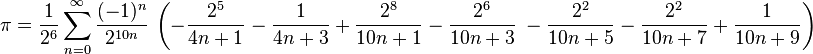
我們將只改變我們的變換公式,其餘的程式碼將保持不變。點這裡下載Python實現的貝拉公式。讓我們來看看bellards(n):
def bellard(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(-1)**k/(1024**k))*( Decimal(256)/(10*k+1)+Decimal(1)/(10*k+9)-Decimal(64)/(10*k+3)-Decimal(32)/(4*k+1)-Decimal(4)/(10*k+5)-Decimal(4)/(10*k+7)-Decimal(1)/(4*k+3))
k+=1
pi=pi*1/(2**6)
return pi輸出結果:
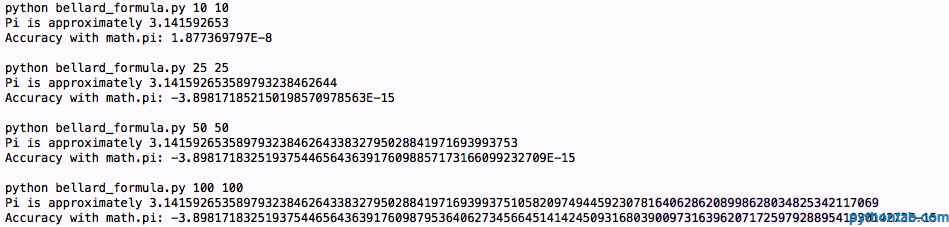
哦,不,我们得到的是同样的精度。好吧,让我们试试第三个公式, Chudnovsky 算法,它看起来是这个样子:
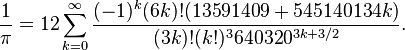
再一次,让我们看一下这个计算公式(假设我们有一个阶乘公式)。 点击这里可下载用 python 实现的 Chudnovsky 公式。
下面是程序和输出结果:
def chudnovsky(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(-1)**k)*(Decimal(factorial(6*k))/((factorial(k)**3)*(factorial(3*k)))*(13591409+545140134*k)/(640320**(3*k)))
k+=1
pi=pi*Decimal(10005).sqrt()/4270934400
pi=pi**(-1)
return pi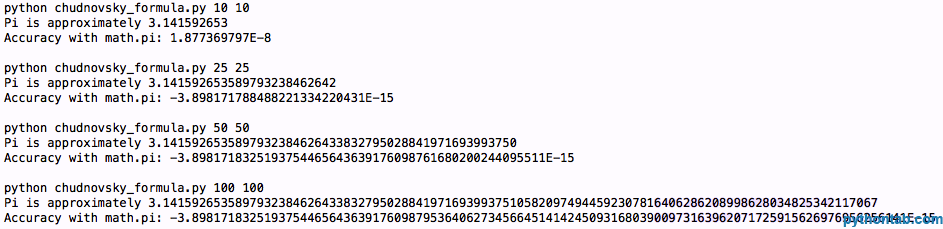
所以我们有了什么结论?花哨的算法不会使机器浮点世界达到更高标准。我真的很期待能有一个比我们用求和公式时所能得到的更好的精度。我猜那是过分的要求。如果你真的需要用PI,就只需使用math.pi变量了。然而,作为乐趣和测试你的计算机真的能有多快,你总是可以尝试第一个计算出Pi的百万位或者更多位是几。




