這篇主要著重在影像的二值化,也就是在灰階化的基礎上,進行閾值分割。二值化的方法很多,事實上,在影像進行處理的時候,能夠完美的分割出目標區域,那麼已經成功了一大半,可見二值化的重要性。本文主要介紹三種二值化方法。
1.固定閾值法,設定好閾值,大於該閾值的像素點設為255,否則為0,這是最簡單的,效果也是最不穩定的。
<span style="font-size:14px;"><span style="font-size:10px;">public void SimBinary(){
toGray();//灰度化
int Threshold = 128;
for (int y = 0; y < h; y++) {
for (int x = 0; x < w; x++) {
if(data[x + y * w] < Threshold){
data[x + y * w] = 0;
}else{
data[x + y * w] = 255;
}
}
}
}</span></span>運作效果如下:
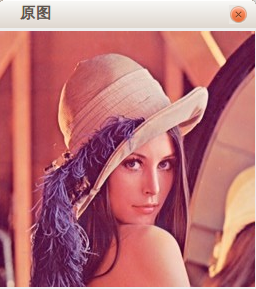

2.循環法(參考:影像處理之常見二值化方法總表)
1. 一個閾值
2. 根據閾值圖每個像素資料P(n,m)分為物件像素資料G1與背景像素資料G2。 (n為
行,m為列)
3. G1的平均值是m1, G2的平均值是m2
4. 一個新的閾值T' = (m1 + m2)/2
5.回到第二步,用新的閾值繼續分像素資料為物件與北京像素數據,繼續2~4步,
直到計算出來的新閾值等於上一次閾值。
程式碼如下:
<span style="max-width:90%"> public void IterBinary(){
toGray();
int Threshold = 128;
int preThreshold = 256;
while (Math.abs(Threshold-preThreshold) > 4){
int s1 = 0;
int s2 = 0;
int f1 = 0;
int f2 = 0;
for (int y = 0; y < h; y++) {
for (int x = 0; x < w; x++) {
if(data[x + y * w] < Threshold){
s1 += data[x + y * w];
f1++;
}else{
s2 += data[x + y * w];
f2++;
}
}
}
preThreshold = Threshold;
Threshold = (int)((s1/f1+s2/f2)/2);
}
for (int y = 0; y < h; y++) {
for (int x = 0; x < w; x++) {
if(data[x + y * w] < Threshold){
data[x + y * w] = 0;
}else{
data[x + y * w] = 255;
}
}
}
}</span>效果如下:

3.大津閾值法(參考:自適應閾值演算法(大津閾值法))
最大類間方差法是由日本學者提出大津於1979年的,是一種自適應的閾值確定的方法,又叫大津法,簡稱OTSU。它是依影像的灰階特性,將影像分成背景和目標2部分。背景與目標之間的類間方差越大,說明構成圖像的2部分的差異越大,當部分目標錯分為背景或部分背景錯分為目標都會導致2部分差別變小。因此,使類間方差最大的分割意味著錯分機率最小。對於影像I(x,y),前景(即目標)和背景的分割閾值記作T,屬於前景的像素點數佔整幅影像的比例記為ω0,其平均灰階μ0;背景像素點數佔整幅影像的比例為ω1,其平均灰度為μ1。影像的總平均值
灰度記為μ,類間變異數記為g。假設影像的背景較暗,且影像的大小為M×N,影像中像素的灰階值小於閾值T的像素個數記作N0,像素灰度大於閾值T的像素個數記作N1,則有:
ω0=N0/ M×N (1)
ω1=N1/ M×N (2)🀎 ω1=N1/ M×N (2) -N
ω0+ω1=1 (4)
μ =ω0*μ0+ω1*μ1 (5)
g=ω0(μ0-μ)^2+ω1(μ1-μ)^2 (6)
將式(5)代入式(6),得到等價公式:
g=ω0ω1(μ0-μ1)^2 (7)
採用遍歷的方法得到使類間方差最大的閾值T,即為所求。
程式碼如下:
<span style="max-width:90%">public void Otsu(){
toGray();
int num = h*w;
int[] hist = hist();
int sum = math.sum(hist);
double[] res = new double[256];
double m1=0,m2=0,w1=0,w2=0;
for(int k=0;k<256;k++){
for(int i=0;i<k;i++){
m1 +=hist[i];
}
w1 = m1/num;
w2 = 1-w1;
m2 = (sum-m1)/(255-k);
m1 = m1/(k+1);
res[k] = w1*w2*Math.abs(m1 - m2)*Math.abs(m1 - m2);
}
int Threshold = math.maxIndex(res); //获得最大值的下标
for (int y = 0; y < h; y++) {
for (int x = 0; x < w; x++) {
if(data[x + y * w] < Threshold){
data[x + y * w] = 0;
}else{
data[x + y * w] = 255;
}
}
}
}</span> 以上就是java 影像的二值化與大津閾值法的內容,更多相關內容請關注PHPcn中文(www.php.)! 




