詳解常用查找資料結構及演算法（Python實作）

一、基本概念

查找（Searching）就是根據給定的某個值，在查找表中確定一個其關鍵字等於給定值的資料元素（或記錄）。

查找表（Search Table）：由相同類型的資料元素（或記錄）構成的集合

關鍵字（Key）：資料元素中某個資料項的值，又稱為鍵值。

主鍵（Primary Key）：可唯一地識別某個資料元素或記錄的關鍵字。

查找表依照操作方式可分為：

靜態查找表（Static Search Table）：只做查找操作的查找表。它的主要操作是：

查詢某個「特定的」資料元素是否在表中

檢索某個「特定的」資料元素和各種屬性

動態查找表（Dynamic Search Table）：在查找中同時進行插入或刪除等操作：

查找時插入資料

查找時刪除資料

二、無序表查找

也就是資料不排序的線性查找，遍歷資料元素。

演算法分析：最好情況是在第一個位置就找到了，此為O(1)；最壞情況在最後一個位置才找到，此為O(n)；所以平均查找次數為(n +1)/2。最終時間複雜度為O(n)

# 最基础的遍历无序列表的查找算法
# 时间复杂度O(n)
 
def sequential_search(lis, key):
  length = len(lis)
  for i in range(length):
    if lis[i] == key:
      return i
    else:
      return False
 
 
if __name__ == '__main__':
  LIST = [1, 5, 8, 123, 22, 54, 7, 99, 300, 222]
  result = sequential_search(LIST, 123)
  print(result)

三、有序表查找

查找表中的資料必須按某個主鍵進行某種排序！

1. 二分查找(​​Binary Search)

演算法核心：在查找表中不斷取中間元素與查找值進行比較，以二分之一的倍率進行表範圍的縮小。

# 针对有序查找表的二分查找算法
# 时间复杂度O(log(n))
 
def binary_search(lis, key):
  low = 0
  high = len(lis) - 1
  time = 0
  while low < high:
    time += 1
    mid = int((low + high) / 2)
    if key < lis[mid]:
      high = mid - 1
    elif key > lis[mid]:
      low = mid + 1
    else:
      # 打印折半的次数
      print("times: %s" % time)
      return mid
  print("times: %s" % time)
  return False
 
if __name__ == &#39;__main__&#39;:
  LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
  result = binary_search(LIST, 99)
  print(result)

2. 插值查找

二分查找法雖然已經很不錯了，但還有可以最佳化的地方。

有的時候，對半過濾還不夠狠，要是每次都排除十分之九的數據豈不是更好？選擇這個值就是關鍵問題，插值的意義就是：以更快的速度進行縮減。

插值的核心就是使用公式：

value = (key - list[low])/(list[high] - list[low])

用這個value來代替二分查找中的1/2。

上面的程式碼可以直接使用，只需改一句。

# 插值查找算法
# 时间复杂度O(log(n))
 
def binary_search(lis, key):
  low = 0
  high = len(lis) - 1
  time = 0
  while low < high:
    time += 1
    # 计算mid值是插值算法的核心代码
    mid = low + int((high - low) * (key - lis[low])/(lis[high] - lis[low]))
    print("mid=%s, low=%s, high=%s" % (mid, low, high))
    if key < lis[mid]:
      high = mid - 1
    elif key > lis[mid]:
      low = mid + 1
    else:
      # 打印查找的次数
      print("times: %s" % time)
      return mid
  print("times: %s" % time)
  return False
 
if __name__ == &#39;__main__&#39;:
  LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
  result = binary_search(LIST, 444)
  print(result)

插值演算法的整體時間複雜度仍屬於O(log(n))層級的。其優點是，對於表內資料量較大，且關鍵字分佈較為均勻的查找表，使用插值演算法的平均效能比二分查找好得多。反之，對於分佈極端不均勻的數據，則不適合使用內插法演算法。

3. 斐波那契查找

由插值演算法帶來的啟發，發明了斐波那契演算法。其核心也是如何優化那個縮減速率，使得查找次數盡量降低。

使用這種演算法，前提是已經有一個包含斐波那契資料的清單

F = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ,...]

# 斐波那契查找算法
# 时间复杂度O(log(n))
 
def fibonacci_search(lis, key):
  # 需要一个现成的斐波那契列表。其最大元素的值必须超过查找表中元素个数的数值。
  F = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,
     233, 377, 610, 987, 1597, 2584, 4181, 6765,
     10946, 17711, 28657, 46368]
  low = 0
  high = len(lis) - 1
   
  # 为了使得查找表满足斐波那契特性，在表的最后添加几个同样的值
  # 这个值是原查找表的最后那个元素的值
  # 添加的个数由F[k]-1-high决定
  k = 0
  while high > F[k]-1:
    k += 1
  print(k)
  i = high
  while F[k]-1 > i:
    lis.append(lis[high])
    i += 1
  print(lis)
   
  # 算法主逻辑。time用于展示循环的次数。
  time = 0
  while low <= high:
    time += 1
    # 为了防止F列表下标溢出，设置if和else
    if k < 2:
      mid = low
    else:
      mid = low + F[k-1]-1
     
    print("low=%s, mid=%s, high=%s" % (low, mid, high))
    if key < lis[mid]:
      high = mid - 1
      k -= 1
    elif key > lis[mid]:
      low = mid + 1
      k -= 2
    else:
      if mid <= high:
        # 打印查找的次数
        print("times: %s" % time)
        return mid
      else:
        print("times: %s" % time)
        return high
  print("times: %s" % time)
  return False
 
if __name__ == &#39;__main__&#39;:
  LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444]
  result = fibonacci_search(LIST, 444)
  print(result)

演算法分析：斐波那契找出的整體時間複雜度也為O(log(n))。但就平均性能，要優於二分查找。但在最壞情況下，例如這裡如果key為1，則始終處於左側半區查找，此時其效率要低於二分查找。

總結：二分查找的mid運算是加法與除法，插值查找則是複雜的四則運算，而斐波那契查找只是最簡單的加減運算。在海量資料的查找中，這種細微的差別可能會影響最終的查找效率。因此，三種有序表的查找方法本質上是分割點的選擇不同，各有優劣，並應根據實際情況進行選擇。

四、線性索引查找

對於海量的無序數據，為了提高查找速度，一般會為其構造索引表。

索引就是把一個關鍵字與它相對應的記錄進行關聯的過程。

一個索引由若干個索引項目構成，每個索引項目至少包含關鍵字和其對應的記錄在記憶體中的位置等資訊。

索引依結構可分為：線性索引、樹狀索引和多層索引。

線性索引：將索引項的集合透過線性結構來組織，也叫索引表。

線性索引可分為：稠密索引、分塊索引和倒排索引

1.稠密索引

稠密索引指的是線性索引中，為資料集合中的每個記錄建立索引項。

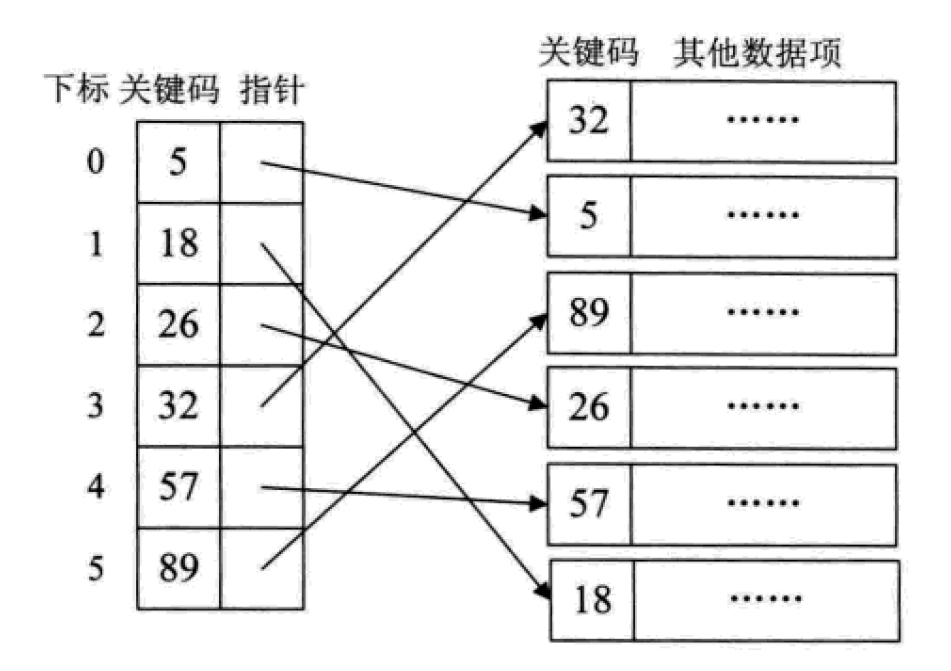
這其實就相當於給無序的集合，建立了一張有序的線性表。其索引項一定是依照關鍵碼進行有序的排列。

這也相當於把查找過程中需要的排序工作給提前做了。

1.分塊索引

給大量的無序資料集合進行分塊處理，使得區塊內無序，區塊與區塊之間有序。

这其实是有序查找和无序查找的一种中间状态或者说妥协状态。因为数据量过大，建立完整的稠密索引耗时耗力，占用资源过多；但如果不做任何排序或者索引，那么遍历的查找也无法接受，只能折中，做一定程度的排序或索引。

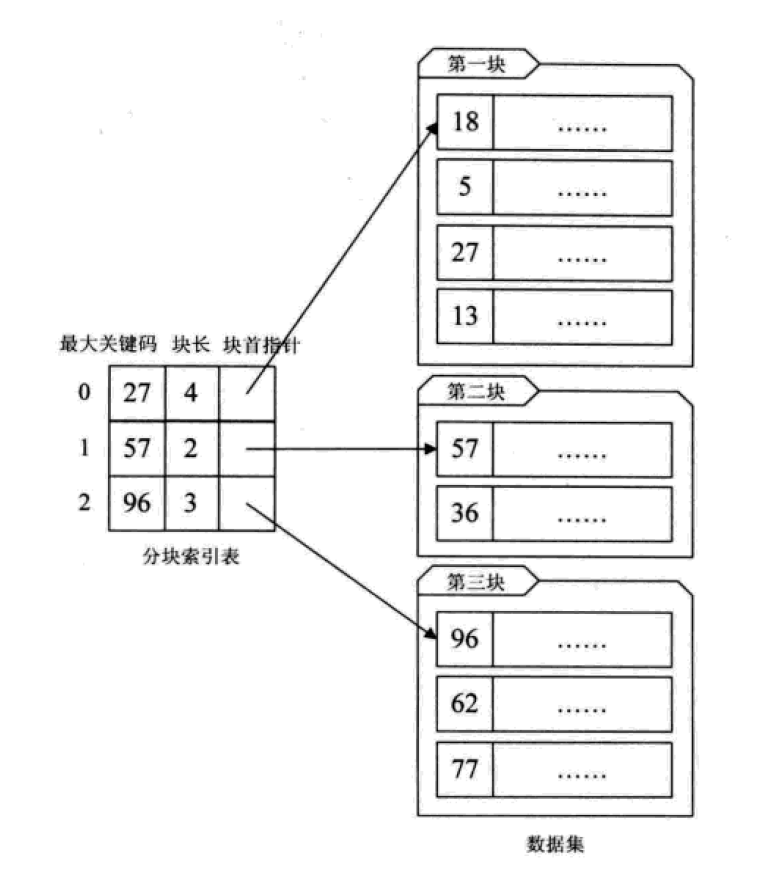
分块索引的效率比遍历查找的O(n)要高一些，但与二分查找的O(logn)还是要差不少。

1.倒排索引

不是由记录来确定属性值，而是由属性值来确定记录的位置，这种被称为倒排索引。其中记录号表存储具有相同次关键字的所有记录的地址或引用（可以是指向记录的指针或该记录的主关键字）。

倒排索引是最基础的搜索引擎索引技术。

五、二叉排序树

二叉排序树又称为二叉查找树。它或者是一颗空树，或者是具有下列性质的二叉树：

若它的左子树不为空，则左子树上所有节点的值均小于它的根结构的值；

若它的右子树不为空，则右子树上所有节点的值均大于它的根结构的值；

它的左、右子树也分别为二叉排序树。

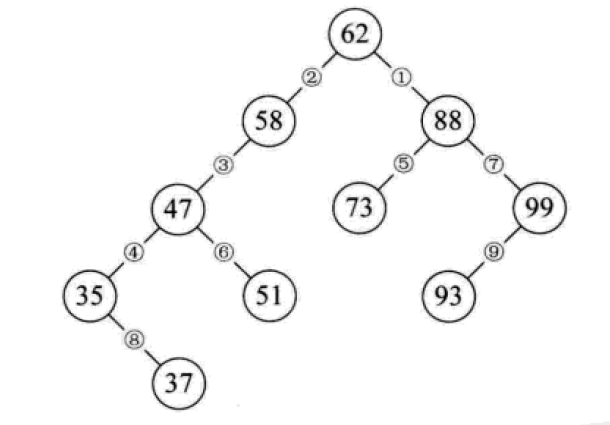
构造一颗二叉排序树的目的，往往不是为了排序，而是为了提高查找和插入删除关键字的速度。

二叉排序树的操作：

1.查找：对比节点的值和关键字，相等则表明找到了；小了则往节点的左子树去找，大了则往右子树去找，这么递归下去，最后返回布尔值或找到的节点。

2.插入：从根节点开始逐个与关键字进行对比，小了去左边，大了去右边，碰到子树为空的情况就将新的节点链接。

3.删除：如果要删除的节点是叶子，直接删；如果只有左子树或只有右子树，则删除节点后，将子树链接到父节点即可；如果同时有左右子树，则可以将二叉排序树进行中序遍历，取将要被删除的节点的前驱或者后继节点替代这个被删除的节点的位置。

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: Liu Jiang
# Python 3.5
 
 
class BSTNode:
  """
  定义一个二叉树节点类。
  以讨论算法为主，忽略了一些诸如对数据类型进行判断的问题。
  """
  def __init__(self, data, left=None, right=None):
    """
    初始化
    :param data: 节点储存的数据
    :param left: 节点左子树
    :param right: 节点右子树
    """
    self.data = data
    self.left = left
    self.right = right
 
 
class BinarySortTree:
  """
  基于BSTNode类的二叉排序树。维护一个根节点的指针。
  """
  def __init__(self):
    self._root = None
 
  def is_empty(self):
    return self._root is None
 
  def search(self, key):
    """
    关键码检索
    :param key: 关键码
    :return: 查询节点或None
    """
    bt = self._root
    while bt:
      entry = bt.data
      if key < entry:
        bt = bt.left
      elif key > entry:
        bt = bt.right
      else:
        return entry
    return None
 
  def insert(self, key):
    """
    插入操作
    :param key:关键码
    :return: 布尔值
    """
    bt = self._root
    if not bt:
      self._root = BSTNode(key)
      return
    while True:
      entry = bt.data
      if key < entry:
        if bt.left is None:
          bt.left = BSTNode(key)
          return
        bt = bt.left
      elif key > entry:
        if bt.right is None:
          bt.right = BSTNode(key)
          return
        bt = bt.right
      else:
        bt.data = key
        return
 
  def delete(self, key):
    """
    二叉排序树最复杂的方法
    :param key: 关键码
    :return: 布尔值
    """
    p, q = None, self._root   # 维持p为q的父节点，用于后面的链接操作
    if not q:
      print("空树！")
      return
    while q and q.data != key:
      p = q
      if key < q.data:
        q = q.left
      else:
        q = q.right
      if not q:        # 当树中没有关键码key时，结束退出。
        return
    # 上面已将找到了要删除的节点，用q引用。而p则是q的父节点或者None（q为根节点时）。
    if not q.left:
      if p is None:
        self._root = q.right
      elif q is p.left:
        p.left = q.right
      else:
        p.right = q.right
      return
    # 查找节点q的左子树的最右节点，将q的右子树链接为该节点的右子树
    # 该方法可能会增大树的深度，效率并不算高。可以设计其它的方法。
    r = q.left
    while r.right:
      r = r.right
    r.right = q.right
    if p is None:
      self._root = q.left
    elif p.left is q:
      p.left = q.left
    else:
      p.right = q.left
 
  def __iter__(self):
    """
    实现二叉树的中序遍历算法,
    展示我们创建的二叉排序树.
    直接使用python内置的列表作为一个栈。
    :return: data
    """
    stack = []
    node = self._root
    while node or stack:
      while node:
        stack.append(node)
        node = node.left
      node = stack.pop()
      yield node.data
      node = node.right
 
 
if __name__ == &#39;__main__&#39;:
  lis = [62, 58, 88, 48, 73, 99, 35, 51, 93, 29, 37, 49, 56, 36, 50]
  bs_tree = BinarySortTree()
  for i in range(len(lis)):
    bs_tree.insert(lis[i])
  # bs_tree.insert(100)
  bs_tree.delete(58)
  for i in bs_tree:
    print(i, end=" ")
  # print("\n", bs_tree.search(4))

二叉排序树总结：

二叉排序树以链式进行存储，保持了链接结构在插入和删除操作上的优点。

在极端情况下，查询次数为1，但最大操作次数不会超过树的深度。也就是说，二叉排序树的查找性能取决于二叉排序树的形状，也就引申出了后面的平衡二叉树。

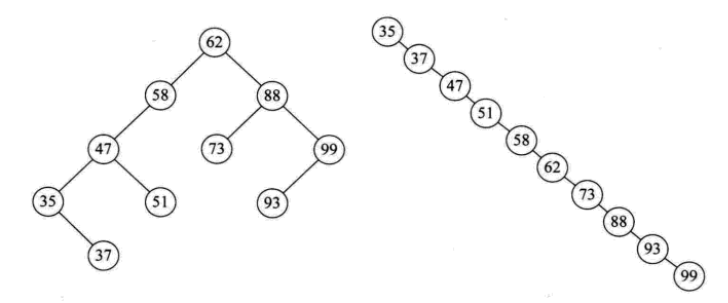
给定一个元素集合，可以构造不同的二叉排序树，当它同时是一个完全二叉树的时候，查找的时间复杂度为O(log(n))，近似于二分查找。

当出现最极端的斜树时，其时间复杂度为O(n)，等同于顺序查找，效果最差。

六、 平衡二叉树

平衡二叉树（AVL树，发明者的姓名缩写）：一种高度平衡的排序二叉树，其每一个节点的左子树和右子树的高度差最多等于1。

平衡二叉树首先必须是一棵二叉排序树！

平衡因子（Balance Factor）：将二叉树上节点的左子树深度减去右子树深度的值。

对于平衡二叉树所有包括分支节点和叶节点的平衡因子只可能是-1,0和1，只要有一个节点的因子不在这三个值之内，该二叉树就是不平衡的。

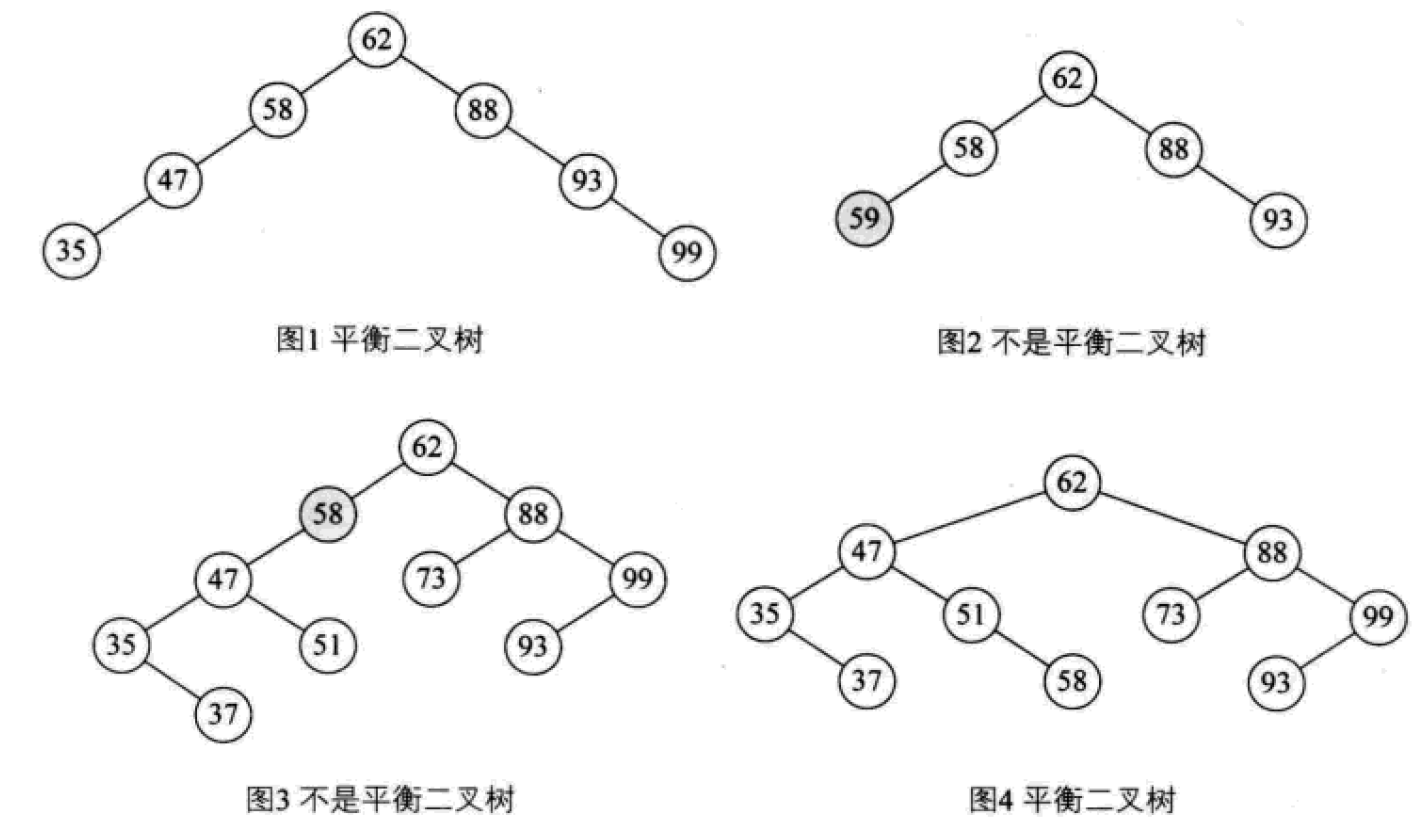
最小不平衡子树：距离插入结点最近的，且平衡因子的绝对值大于1的节点为根的子树。

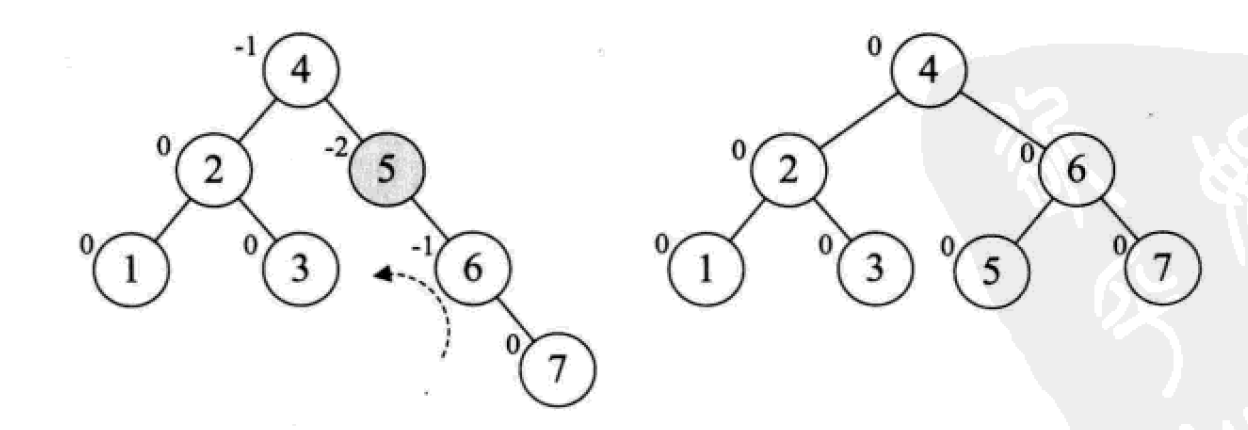
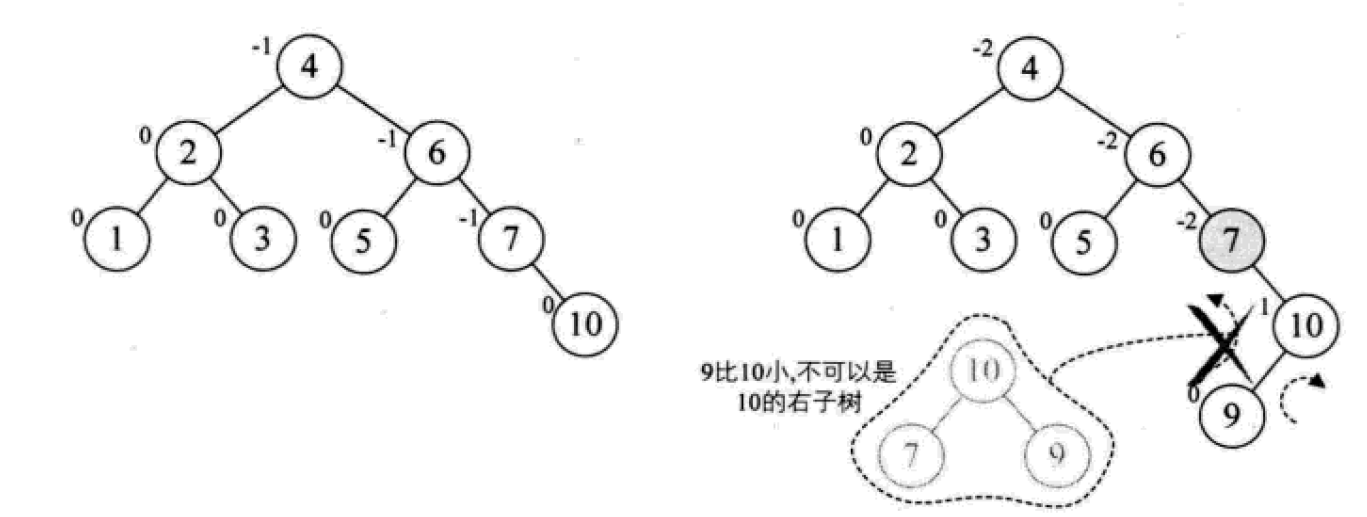
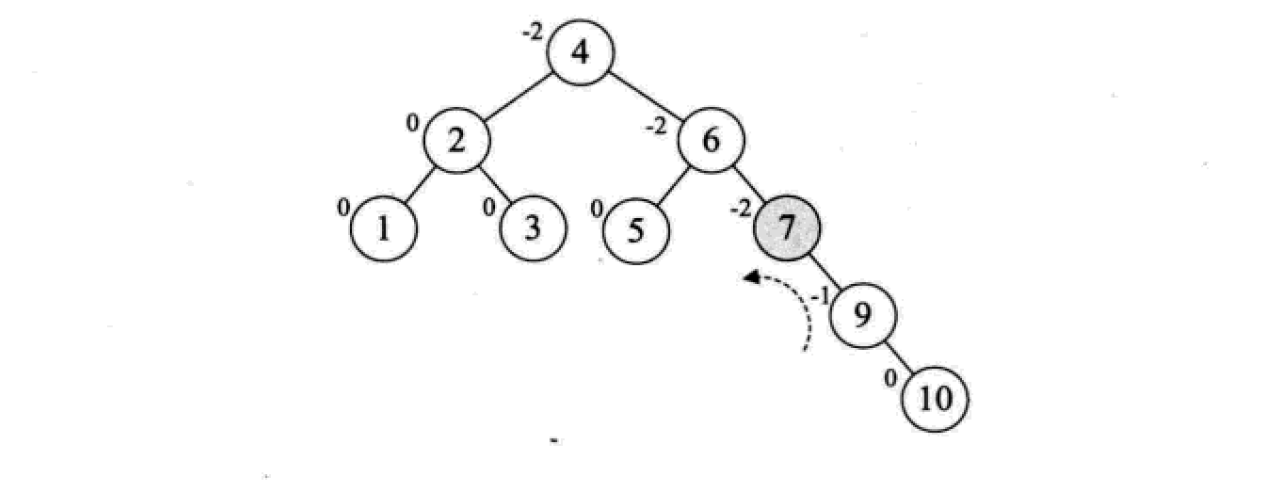
平衡二叉树的构建思想：每当插入一个新结点时，先检查是否破坏了树的平衡性，若有，找出最小不平衡子树。在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点之间的连接关系，进行相应的旋转，成为新的平衡子树。

下面是由[1,2,3,4,5,6,7,10,9]构建平衡二叉树

）其每一個節點的孩子可以多於兩個，每一個結點可以儲存多個元素。

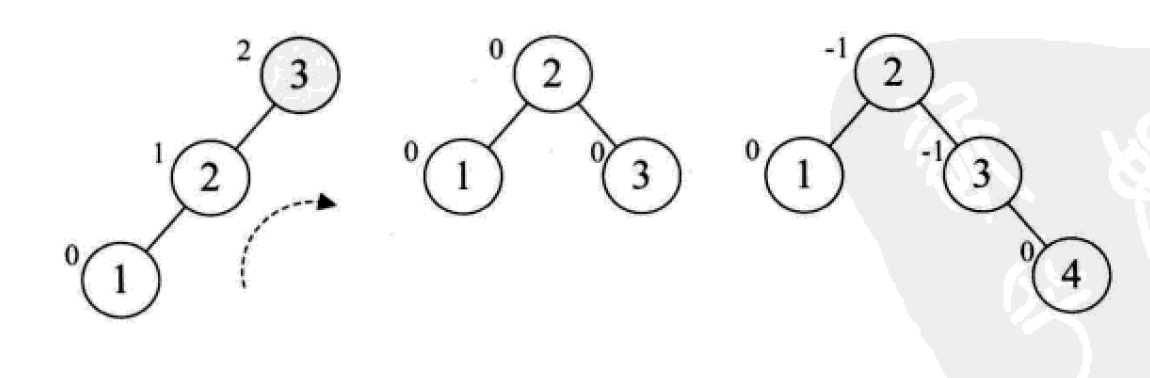
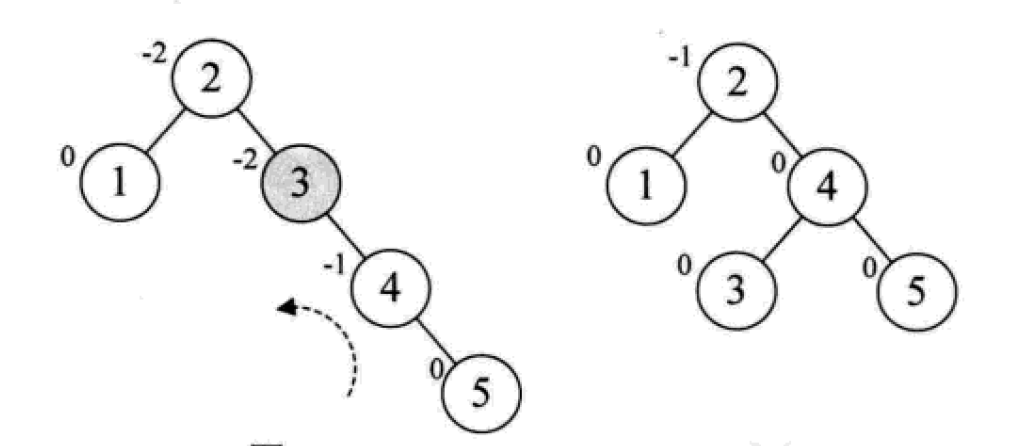
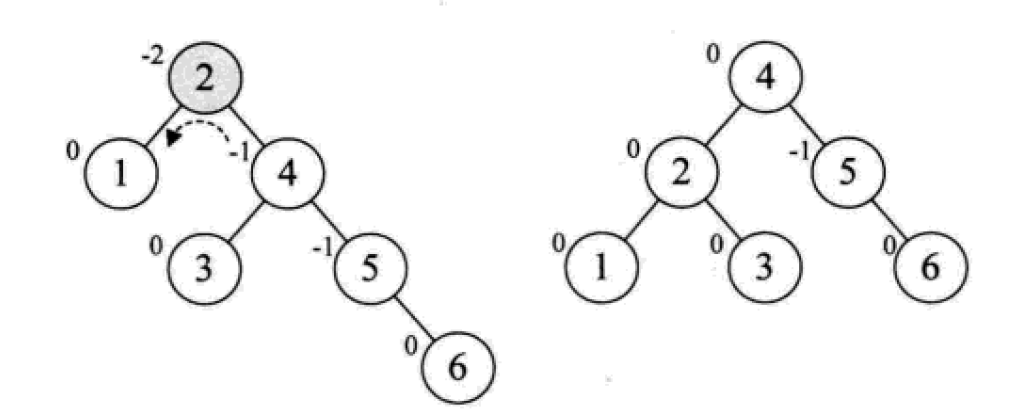
 對於多路查找樹，每個節點可以儲存多少個元素，以及它的孩子數的多少是關鍵，常用的有這4種形式：2-3樹、2-3-4樹、B樹和B+樹。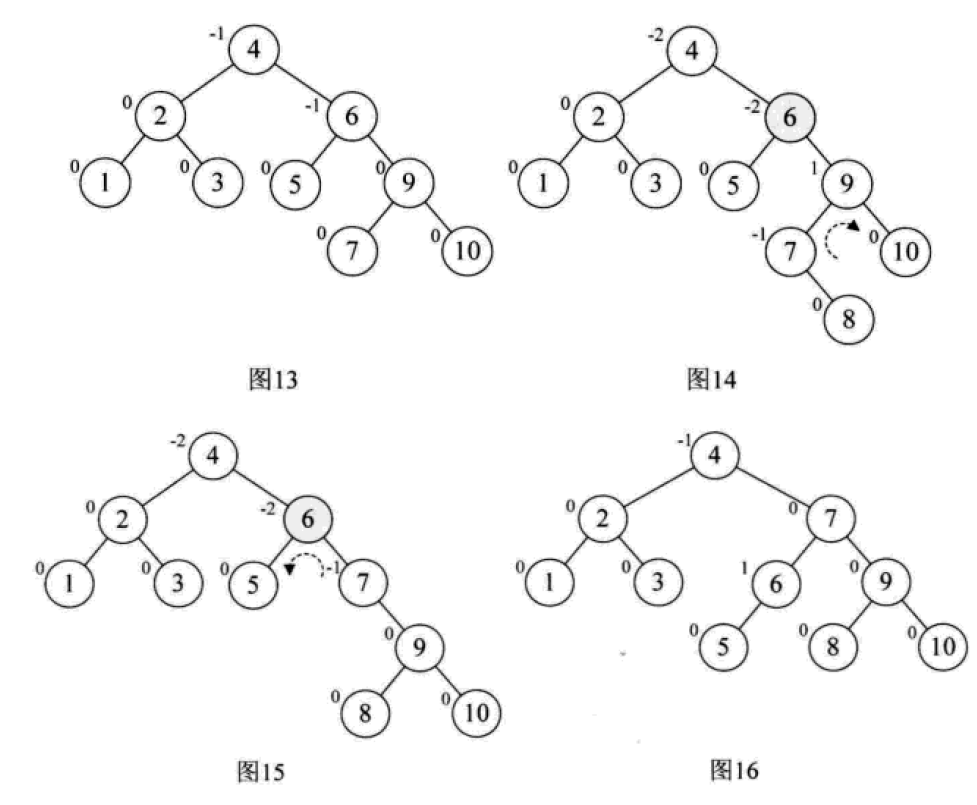

2-3樹

2-3樹：每個結點都有2個孩子，或3個孩子，或沒有孩子。

一個2結點包含一個元素和兩個孩子（或沒有孩子，不能只有一個孩子）。與二元排序樹類似，其左子樹包含的元素都小於該元素，右子樹包含的元素都大於該元素。

一個3結點包含兩個元素和三個孩子（或沒有孩子，不能只有一個或兩個孩子）。

2-3樹中所有的葉子都必須在同一層次上。

其插入操作如下：

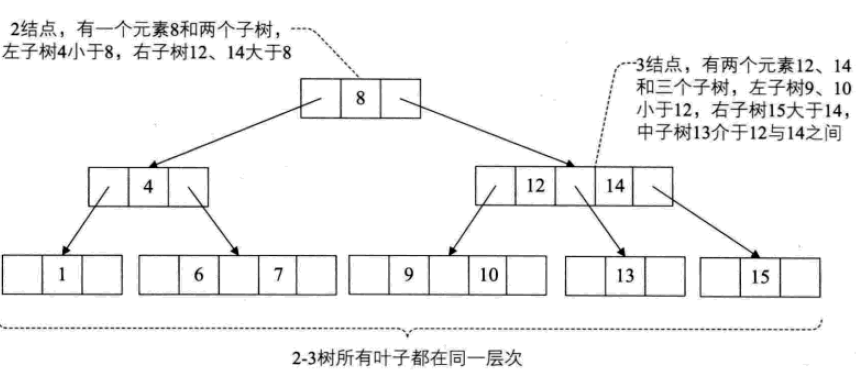
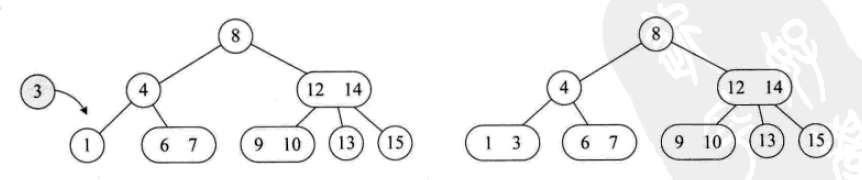
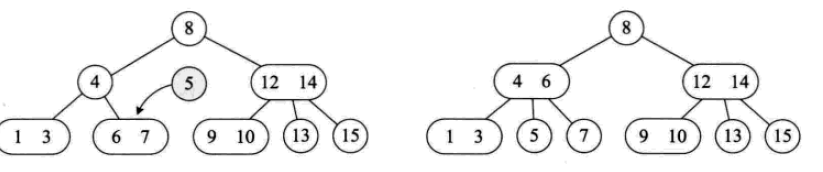
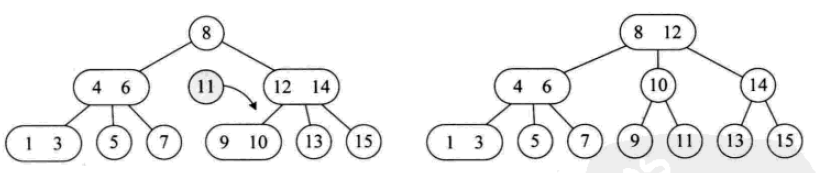
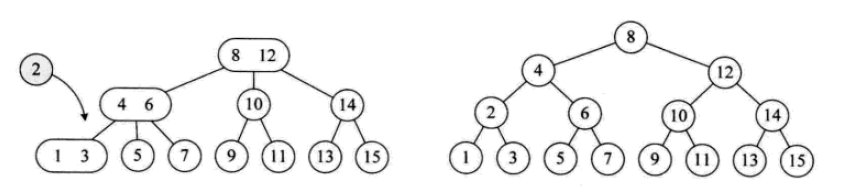
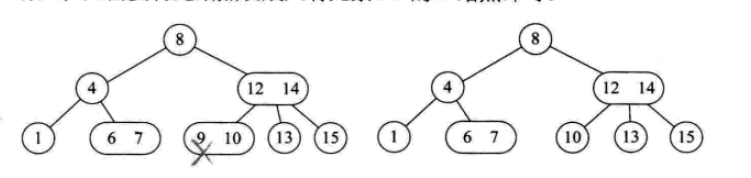
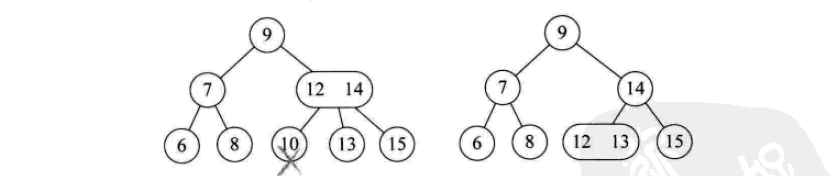
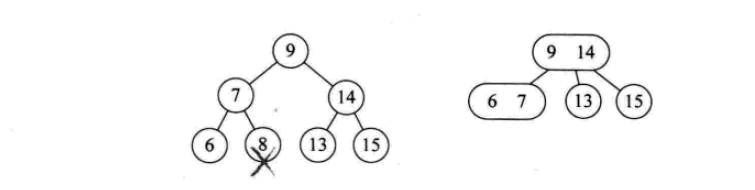
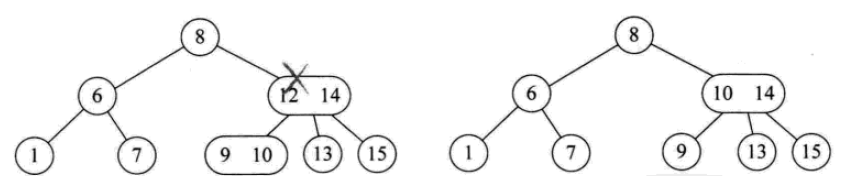
2-3-4樹

其實的使用2-34-34-34-34-34-34-34-34-34-34-34-342-342-342-34點的樹結。一個4個結點包含小中大三個元素和四個孩子（或沒有孩子）。

其插入操作:

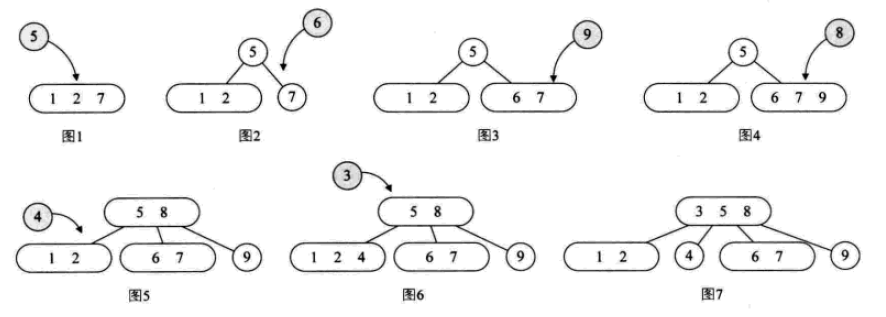
其刪除操作：

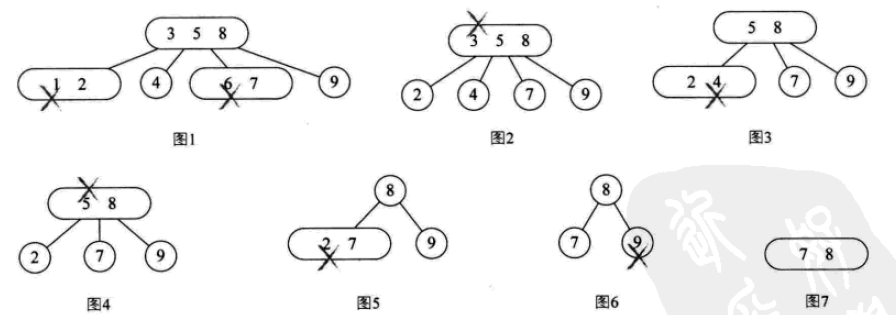
B樹

B樹是一種平衡的多路查找樹。節點最大的孩子數目稱為B樹的階（order）。 2-3樹是3階B樹，2-3-4是4階B樹。

B樹的資料結構主要用在記憶體和外部記憶體的資料互動中。

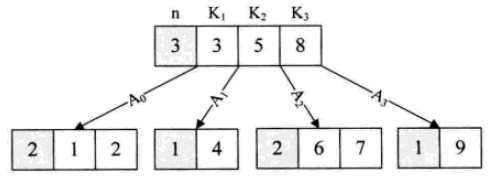
B+樹

為了解決B樹的所有元素組織等基本問題，在原歷等基本問題，在原始的結構基礎上，加入新的元素組織方式後，形成了B+樹曆。

B+樹是應文件系統所需而出現的一種B樹的變形樹，嚴格意義上將，它已經不是最基本的樹了。

B+樹中，出現在分支節點中的元素會被當作他們在該分支節點位置的中序後繼者（葉子節點）中再次列出。另外，每一個葉子節點都會保存一個指向後一葉節點的指標。

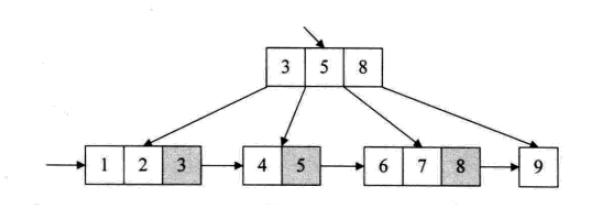
所有的葉子節點包含全部的關鍵字的信息，及相關指針，葉子節點本身依關鍵字的大小自小到大順序鏈接

B+樹的結構特別適合帶有範圍的查找。例如查找年齡在20~30歲之間的人。

八、散列表（雜湊表）

散列表：所有的元素之間沒有任何關係。元素的儲存位置，是利用元素的關鍵字透過某個函數直接計算出來的。這個一一對應的關係函數稱為雜湊函數或Hash函數。

採用雜湊技術將記錄儲存在一塊連續的儲存空間中，稱為雜湊表或雜湊表（Hash Table）。關鍵字對應的儲存位置，稱為雜湊位址。

散列表是一種面向查找的儲存結構。它最適合求解的問題是尋找與給定值相等的記錄。但是某個關鍵字能對應很多記錄的情況就不適用，例如找出所有的「男」性。也不適合範圍查找，例如查找年齡20~30之間的人。排序、最大、最小等也不合適。

因此，散列表通常用於關鍵字不重複的資料結構。例如python的字典資料型別。

設計出一個簡單、均勻、儲存利用率高的雜湊函數是雜湊技術中最關鍵的問題。

 但是，一般雜湊函數都面臨衝突的問題。

衝突：兩個不同的關鍵字，透過雜湊函數計算後結果卻相同的現象。 collision。

8.1 雜湊函數的建構方法

好的雜湊函數：計算簡單、雜湊位址分佈均勻

1.直接定址法

 例如取關鍵字的某個線性函數為雜湊函數：

f(key) = a*key + b (a,b為常數）

2.数字分析法

抽取关键字里的数字，根据数字的特点进行地址分配

3.平方取中法

将关键字的数字求平方，再截取部分

4.折叠法

将关键字的数字分割后分别计算，再合并计算，一种玩弄数字的手段。

5.除留余数法

最为常见的方法之一。

对于表长为m的数据集合，散列公式为：

f(key) = key mod p (p<=m)

mod：取模（求余数）

该方法最关键的是p的选择，而且数据量较大的时候，冲突是必然的。一般会选择接近m的质数。

6.随机数法

选择一个随机数，取关键字的随机函数值为它的散列地址。

f(key) = random(key)

总结，实际情况下根据不同的数据特性采用不同的散列方法，考虑下面一些主要问题：

计算散列地址所需的时间

关键字的长度

散列表的大小

关键字的分布情况

记录查找的频率

8.2 处理散列冲突

1、开放定址法

就是一旦发生冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。

公式是：

这种简单的冲突解决办法被称为线性探测，无非就是自家的坑被占了，就逐个拜访后面的坑，有空的就进，也不管这个坑是不是后面有人预定了的。

线性探测带来的最大问题就是冲突的堆积，你把别人预定的坑占了，别人也就要像你一样去找坑。

改进的办法有二次方探测法和随机数探测法。

2、再散列函数法

发生冲突时就换一个散列函数计算，总会有一个可以把冲突解决掉，它能够使得关键字不产生聚集，但相应地增加了计算的时间。

3、链接地址法
碰到冲突时，不更换地址，而是将所有关键字为同义词的记录存储在一个链表里，在散列表中只存储同义词子表的头指针，如下图：

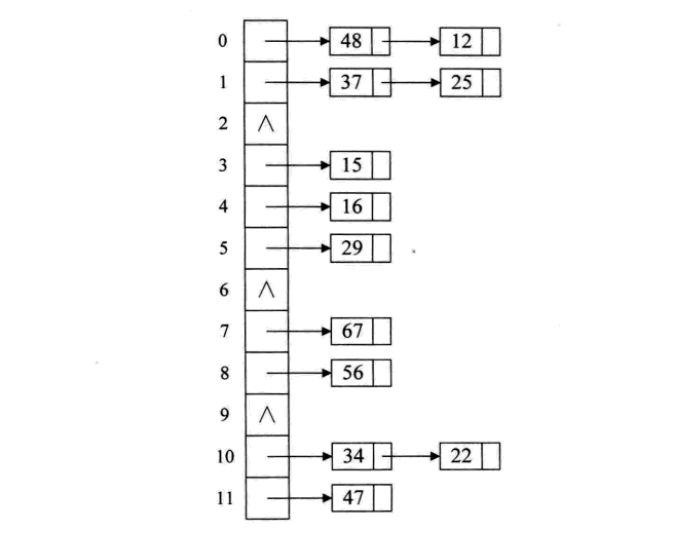
这样的好处是，不怕冲突多；缺点是降低了散列结构的随机存储性能。本质是用单链表结构辅助散列结构的不足。

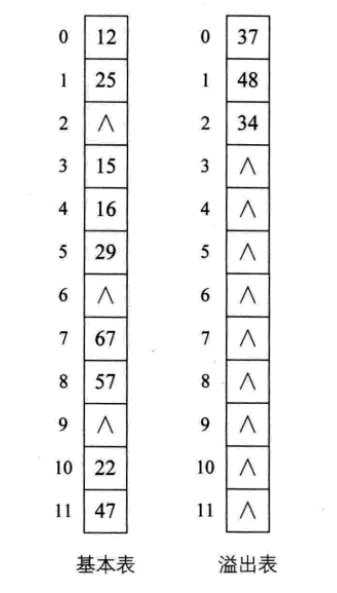
4、公共溢出区法

其实就是为所有的冲突，额外开辟一块存储空间。如果相对基本表而言，冲突的数据很少的时候，使用这种方法比较合适。

8.3 散列表查找实现

下面是一段简单的实现代码：

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: Liu Jiang
# Python 3.5
# 忽略了对数据类型，元素溢出等问题的判断。
 
 
class HashTable:
  def __init__(self, size):
    self.elem = [None for i in range(size)] # 使用list数据结构作为哈希表元素保存方法
    self.count = size # 最大表长
 
  def hash(self, key):
    return key % self.count # 散列函数采用除留余数法
 
  def insert_hash(self, key):
    """插入关键字到哈希表内"""
    address = self.hash(key) # 求散列地址
    while self.elem[address]: # 当前位置已经有数据了，发生冲突。
      address = (address+1) % self.count # 线性探测下一地址是否可用
    self.elem[address] = key # 没有冲突则直接保存。
 
  def search_hash(self, key):
    """查找关键字，返回布尔值"""
    star = address = self.hash(key)
    while self.elem[address] != key:
      address = (address + 1) % self.count
      if not self.elem[address] or address == star: # 说明没找到或者循环到了开始的位置
        return False
    return True
 
 
if __name__ == '__main__':
  list_a = [12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34]
  hash_table = HashTable(12)
  for i in list_a:
    hash_table.insert_hash(i)
 
  for i in hash_table.elem:
    if i:
      print((i, hash_table.elem.index(i)), end=" ")
  print("\n")
 
  print(hash_table.search_hash(15))
  print(hash_table.search_hash(33))

   

8.4 散列表查找性能分析

如果没发生冲突，则其查找时间复杂度为O(1)，属于最极端的好了。

但是，现实中冲突可不可避免的，下面三个方面对查找性能影响较大：

散列函数是否均匀

处理冲突的办法

散列表的装填因子（表内数据装满的程度）

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持PHP中文网。

更多詳解常用查找資料結構及演算法（Python實作）相关文章请关注PHP中文网！