之前簡單介紹了動態規劃的概念和解題步驟,但是學習中感覺動態規劃的應用範圍太靈活了,這裡就挑一些常見的題目多練習一下。
1、最長公共子序列(字串相關)
給出兩個字串,找出最長公共子序列(LCS),傳回LCS的長度。例如:
例如:給"ABCD"和"EDCA",這個LCS是"A"(或D或C),返回1;
給"ABCD" 和"EACB",這個LCS是"AC"返回2 。
思路:長度為m的字串a和長度為n的字串b,他們的最長公共子序列longest[m][n]可透過m-1長度的a和n-1長度的b推得:當a[m]等於b[n]的時候,longest[m][n] = longest[m-1][n-1] + 1;當a[m]不等於b[n]時, longest[m][n]=max(longest[m-1][n], longest[m][n-1])。當字串a或b為空字串時,它與另一個字串的最長公共子序列必然是0。最後題目的解即為longest[strlen(a)][strlen(b)]。
程式碼:
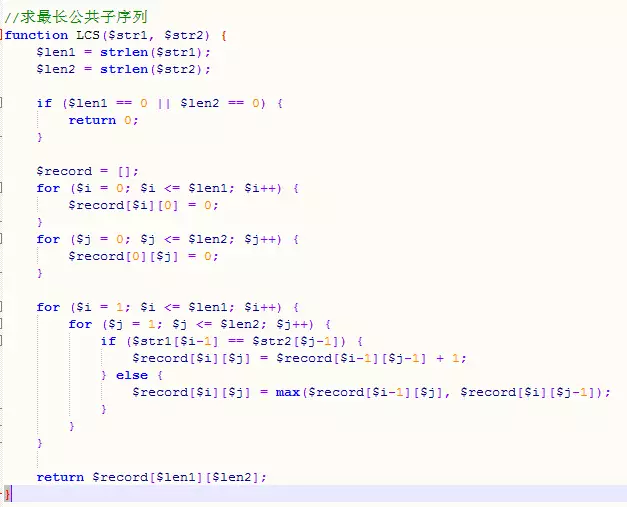
2、編輯距離(字串相關)
給出兩個單字word1和word2,計算出將word1 轉換為word2的最少操作次數。
你總共三種操作方法:插入一個字元、刪除一個字元、取代一個字元。
例如:給出 work1="mart" 和 work2="karma",回傳 3。
思路:對於長度為m的字串a和長度為n的字串b(m、n都大於0),如果a[m]不等於b[n],那麼a變成b的最小操作次數=min(a[m-1]變成b[n]的最小操作次數+1,a[m]變成b[n-1]的最小操作次數+1,a[m-1]變成b [n-1]的最小操作次數);如果a[m]等於b[n],那麼a[m]變成b[n]的最小操作次數=a[m-1]變成b[n- 1]的最小操作次數。
代碼:
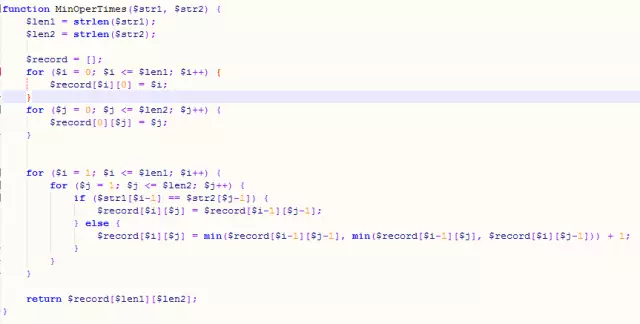
3、背包問題
給出n個物品的體積A[i]和其價值V[i],將他們裝入一個大小為m的背包,最多能裝入的總價值有多大?
例如:對於物品體積[2, 3, 5, 7]和對應的價值[1, 5, 2, 4], 假設背包大小為10的話,最大能夠裝入的價值為9。
思路:當空間為v時,對於任一個物品i,如果i可以放入(v大於等於weight[i]),則此時v空間的價值f(v)等於f(v-weight[i ]) + values[i],因此透過遍歷全部物品可以找到在空間為v時所能得到的最大值。
代碼:
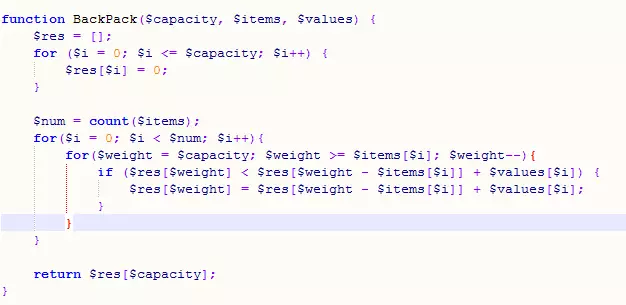
4、區間問題(Google面試題)
有n個硬幣排成一條線,每一枚硬幣有不同的價值。兩位參賽者輪流一從任何一邊拿一枚硬幣,直到沒有硬幣為止。計算拿到的硬幣總價值,價值最高的勝利。請判定第一位玩家是輸還是贏?
例如:給定陣列[3,2,2],傳回true;給定陣列[1,20,15],傳回false。
思路:對於給定的一個閉區間(i到j,j大於等於i),玩家A拿硬幣只有兩種拿法,從左拿或從右拿。如果從左拿,則A能拿到的最大面值=拿到的這枚硬幣的面值+ 剩餘區間的總面值- B玩家在剩餘區間能拿到的最大面值;A從右拿的情況與從左拿類似。由此我們可以得到狀態轉移方程式。而透過兩個循環我們能夠得到長度為n的序列裡任意i到j區間的面值總和,以及j=i的情況下先手玩家拿到的最大值(即第i個硬幣的面值)。
程式碼:
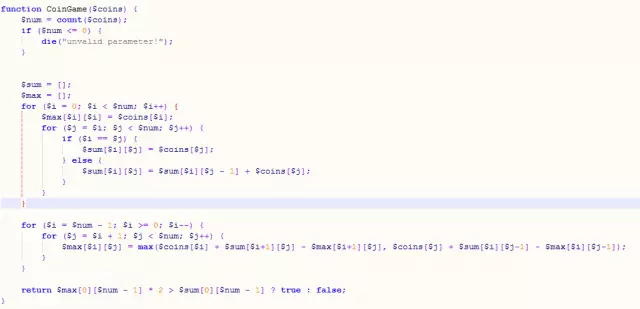
以上就是php演算法學習動態規劃(二)的內容,更多相關內容請關注PHP中文網(www.php.cn)!




