---------------------------------------- -------------------------------------------------- -------------------------------------------------- --------------------------------
TreeMap的實作是紅黑樹演算法的實現,所以要了解TreeMap就必須對紅黑樹有一定的了解,其實這篇博文的名字叫做:根據紅黑樹的算法來分析TreeMap的實現,但是為了與Java提高篇系列博文保持一致還是叫做TreeMap比較好。透過這篇文章你可以獲得以下知識要點:
1、紅黑樹的基本概念。
2、紅黑樹增加節點、刪除節點的實現過程。
3、紅黑樹左旋、右旋的複雜過程。
4、Java 中TreeMap是如何透過put、deleteEntry兩個來實現紅黑樹增加、刪除節點的。
我想透過這篇博文你對TreeMap一定有了更深的認識。好了,下面先簡單普及紅黑樹知識。
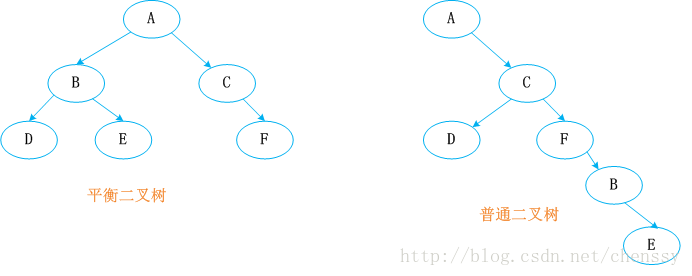
一叉樹蠔 同時紅黑樹更是一顆自平衡的排序二元樹。
我們知道一個基本的二元樹他們都需要滿足一個基本性質--即樹中的任何節點的值大於它的左子節點,並且小於它的右子節點。依照這個基本性質使得樹的檢索效率大大提升。我們知道在生成二元樹的過程是非常容易失衡的,最壞的情況就是一邊倒(只有右/左子樹),這樣勢必會導致二元樹的檢索效率大大降低(O(n)),所以為了維持二元樹的平衡,大牛提出了各種實現的演算法,如:AVL,SBT,伸展樹,TREAP ,紅黑樹等等。
平衡二元樹必須具備以下特性:它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1,並且左右兩個子樹都是一棵平衡二元樹。也就是說該二元樹的任何一個等等子節點,其左右子樹的高度都相近。
紅黑樹顧名思義是節點是紅色或黑色的平衡二元樹,而它透過顏色的限制來維持著二叉樹的平衡。一棵有效的紅黑樹二叉樹而言我們必須增加以下規則:
1、每個節點只能是紅色或黑色
2、根節點是黑色3、每個葉節點(NIL節點,節點節點)是黑色的。
4、如果一個結點是紅的,則它兩個子節點都是黑的。也就是說一條路徑上不能出現相鄰的兩個紅色結點。
5、從任何節點到其每個葉子的所有路徑都包含相同數目的黑色節點。
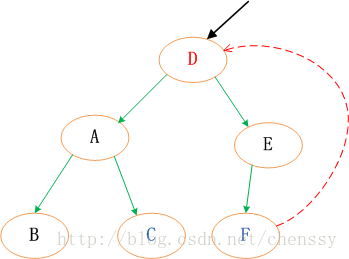
這些約束強制了紅黑樹的關鍵性質: 從根到葉子的最長的可能路徑不多於最短的可能路徑的兩倍長。結果是這棵樹大致上是平衡的。因為操作例如插入、刪除和查找某個值的最壞情況時間都要求與樹的高度成比例,這個在高度上的理論上限允許紅黑樹在最壞情況下都是高效的,而不同於普通的二元查找樹。所以紅黑樹它是複雜而有效率的,其檢索效率O(log n)。下圖為一顆典型的紅色黑色二元樹。 對於紅黑二叉樹而言它主要包括三旋大基本操作:左旋和右旋著色。 左旋 (圖片來自:http://www.php.cn/)
本節參考文獻:httphttp ://www.php.cn/百度百科 註:由於本文主要是講解中對黑樹,如果 2、紅黑樹資料結構剖面3、紅黑樹 二、TreeMap資料結構 >>>>>>回歸主角:TreeMap
TreeMap Map繼承AbstractMap,實作NavigableMap、Cloneable、Serializable三個介面。其中AbstractMap顯示TreeMap為一個Map即支援key-value的集合, NavigableMap(更多)則表示它支援一系列的導航方法,具備針對給定搜尋目標傳回最接近匹配項的導航方法 。
//比较器,因为TreeMap是有序的,通过comparator接口我们可以对TreeMap的内部排序进行精密的控制 private final Comparator<? super K> comparator; //TreeMap红-黑节点,为TreeMap的内部类 private transient Entry<K,V> root = null; //容器大小 private transient int size = 0; //TreeMap修改次数 private transient int modCount = 0; //红黑树的节点颜色--红色 private static final boolean RED = false; //红黑树的节点颜色--黑色 private static final boolean BLACK = true;
对于叶子节点Entry是TreeMap的内部类,它有几个重要的属性:
//键 K key; //值 V value; //左孩子 Entry<K,V> left = null; //右孩子 Entry<K,V> right = null; //父亲 Entry<K,V> parent; //颜色 boolean color = BLACK;
注:前面只是开胃菜,下面是本篇博文的重中之重,在下面两节我将重点讲解treeMap的put()、delete()方法。通过这两个方法我们会了解红黑树增加、删除节点的核心算法。
在了解TreeMap的put()方法之前,我们先了解红黑树增加节点的算法。
红黑树在新增节点过程中比较复杂,复杂归复杂它同样必须要依据上面提到的五点规范,同时由于规则1、2、3基本都会满足,下面我们主要讨论规则4、5。假设我们这里有一棵最简单的树,我们规定新增的节点为N、它的父节点为P、P的兄弟节点为U、P的父节点为G。
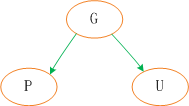
对于新节点的插入有如下三个关键地方:
1、插入新节点总是红色节点 。
2、如果插入节点的父节点是黑色, 能维持性质 。
3、如果插入节点的父节点是红色, 破坏了性质. 故插入算法就是通过重新着色或旋转, 来维持性质 。
为了保证下面的阐述更加清晰和根据便于参考,我这里将红黑树的五点规定再贴一遍:
1、每个节点都只能是红色或者黑色
2、根节点是黑色
3、每个叶节点(NIL节点,空节点)是黑色的。
4、如果一个结点是红的,则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
一、为跟节点
若新插入的節點N沒有父節點,直接當做根據節點插入即可,同時將顏色設為黑色。 (如圖一(1))
二、父這種情況新節點N同樣是直接插入,同時顏色為紅色,由於根據規則四它會存在兩個黑色的葉子節點,值為null。同時由於新增節點N為紅色,所以通過它的子節點的路徑仍會保存相同的黑色節點數,同樣滿足規則5。 (如圖一(2))
(圖一)
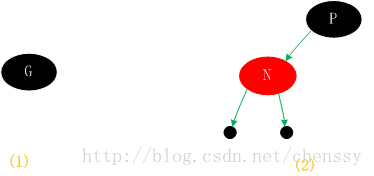
對於此情況若直接插入一定會出現不平衡現象。怎麼處理? P、U節點變黑、G節點變紅。這時由於經過節點P、U的路徑都必須經過G所以在這些路徑上面的黑節點數目還是相同的。但是經過上面的處理,可能G節點的父節點也是紅色,這時候我們需要將G節點當作新增節點遞歸處理。
四、若父節點為黑色,叔父節點為節或缺少
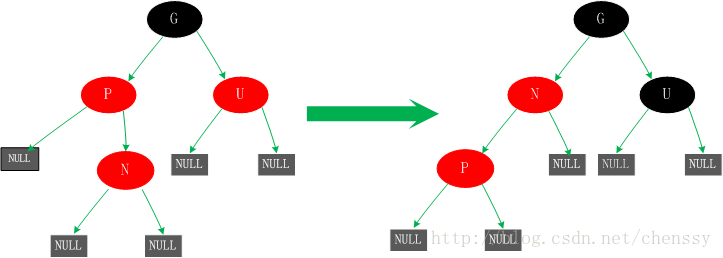
 對於這種情況我們對新增節點N、P進行一次左旋轉。這裡所產生的結果其實並沒有完成,還不是平衡的(違反了規則四),這是我們需要進行情況5的操作。
對於這種情況我們對新增節點N、P進行一次左旋轉。這裡所產生的結果其實並沒有完成,還不是平衡的(違反了規則四),這是我們需要進行情況5的操作。
在TreeMap的put()的实现方法中主要分为两个步骤,第一:构建排序二叉树,第二:平衡二叉树。 TreeMap put()方法实现分析
对于排序二叉树的创建,其添加节点的过程如下:
1、以根节点为初始节点进行检索。
2、与当前节点进行比对,若新增节点值较大,则以当前节点的右子节点作为新的当前节点。否则以当前节点的左子节点作为新的当前节点。
3、循环递归2步骤知道检索出合适的叶子节点为止。
4、将新增节点与3步骤中找到的节点进行比对,如果新增节点较大,则添加为右子节点;否则添加为左子节点。
按照这个步骤我们就可以将一个新增节点添加到排序二叉树中合适的位置。如下:
public V put(K key, V value) {
//用t表示二叉树的当前节点
Entry<K,V> t = root;
//t为null表示一个空树,即TreeMap中没有任何元素,直接插入
if (t == null) {
//比较key值,个人觉得这句代码没有任何意义,空树还需要比较、排序?
compare(key, key); // type (and possibly null) check
//将新的key-value键值对创建为一个Entry节点,并将该节点赋予给root
root = new Entry<>(key, value, null);
//容器的size = 1,表示TreeMap集合中存在一个元素
size = 1;
//修改次数 + 1
modCount++;
return null;
}
int cmp; //cmp表示key排序的返回结果
Entry<K,V> parent; //父节点
// split comparator and comparable paths
Comparator<? super K> cpr = comparator; //指定的排序算法
//如果cpr不为空,则采用既定的排序算法进行创建TreeMap集合
if (cpr != null) {
do {
parent = t; //parent指向上次循环后的t
//比较新增节点的key和当前节点key的大小
cmp = cpr.compare(key, t.key);
//cmp返回值小于0,表示新增节点的key小于当前节点的key,则以当前节点的左子节点作为新的当前节点
if (cmp < 0)
t = t.left;
//cmp返回值大于0,表示新增节点的key大于当前节点的key,则以当前节点的右子节点作为新的当前节点
else if (cmp > 0)
t = t.right;
//cmp返回值等于0,表示两个key值相等,则新值覆盖旧值,并返回新值
else
return t.setValue(value);
} while (t != null);
}
//如果cpr为空,则采用默认的排序算法进行创建TreeMap集合
else {
if (key == null) //key值为空抛出异常
throw new NullPointerException();
/* 下面处理过程和上面一样 */
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//将新增节点当做parent的子节点
Entry<K,V> e = new Entry<>(key, value, parent);
//如果新增节点的key小于parent的key,则当做左子节点
if (cmp < 0)
parent.left = e;
//如果新增节点的key大于parent的key,则当做右子节点
else
parent.right = e;
/*
* 上面已经完成了排序二叉树的的构建,将新增节点插入该树中的合适位置
* 下面fixAfterInsertion()方法就是对这棵树进行调整、平衡,具体过程参考上面的五种情况
*/
fixAfterInsertion(e);
//TreeMap元素数量 + 1
size++;
//TreeMap容器修改次数 + 1
modCount++;
return null;
}上面代码中do{}代码块是实现排序二叉树的核心算法,通过该算法我们可以确认新增节点在该树的正确位置。找到正确位置后将插入即可,这样做了其实还没有完成,因为我知道TreeMap的底层实现是红黑树,红黑树是一棵平衡排序二叉树,普通的排序二叉树可能会出现失衡的情况,所以下一步就是要进行调整。fixAfterInsertion(e); 调整的过程务必会涉及到红黑树的左旋、右旋、着色三个基本操作。代码如下:
/**
* 新增节点后的修复操作
* x 表示新增节点
*/
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED; //新增节点的颜色为红色
//循环 直到 x不是根节点,且x的父节点不为红色
while (x != null && x != root && x.parent.color == RED) {
//如果X的父节点(P)是其父节点的父节点(G)的左节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//获取X的叔节点(U)
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
//如果X的叔节点(U) 为红色(情况三)
if (colorOf(y) == RED) {
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的叔节点(U)设置为黑色
setColor(y, BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
//如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五)
else {
//如果X节点为其父节点(P)的右子树,则进行左旋转(情况四)
if (x == rightOf(parentOf(x))) {
//将X的父节点作为X
x = parentOf(x);
//右旋转
rotateLeft(x);
}
//(情况五)
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
//以X的父节点的父节点(G)为中心右旋转
rotateRight(parentOf(parentOf(x)));
}
}
//如果X的父节点(P)是其父节点的父节点(G)的右节点
else {
//获取X的叔节点(U)
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
//如果X的叔节点(U) 为红色(情况三)
if (colorOf(y) == RED) {
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的叔节点(U)设置为黑色
setColor(y, BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
//如果X的叔节点(U为黑色);这里会存在两种情况(情况四、情况五)
else {
//如果X节点为其父节点(P)的右子树,则进行左旋转(情况四)
if (x == leftOf(parentOf(x))) {
//将X的父节点作为X
x = parentOf(x);
//右旋转
rotateRight(x);
}
//(情况五)
//将X的父节点(P)设置为黑色
setColor(parentOf(x), BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
//以X的父节点的父节点(G)为中心右旋转
rotateLeft(parentOf(parentOf(x)));
}
}
}
//将根节点G强制设置为黑色
root.color = BLACK;
}对这段代码的研究我们发现,其处理过程完全符合红黑树新增节点的处理过程。所以在看这段代码的过程一定要对红黑树的新增节点过程有了解。在这个代码中还包含几个重要的操作。左旋(rotateLeft())、右旋(rotateRight())、着色(setColor())。
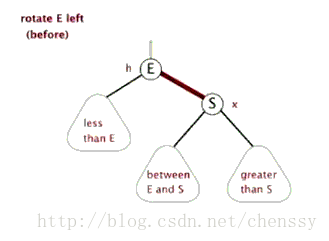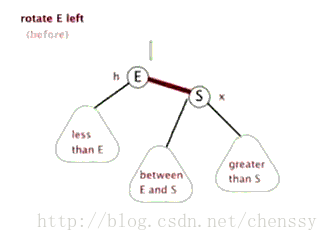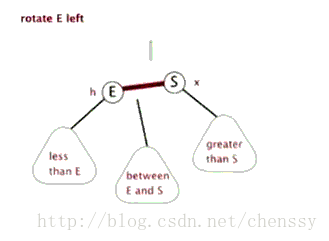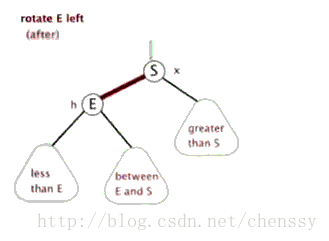
左旋:rotateLeft()
所谓左旋转,就是将新增节点(N)当做其父节点(P),将其父节点P当做新增节点(N)的左子节点。即:G.left ---> N ,N.left ---> P。
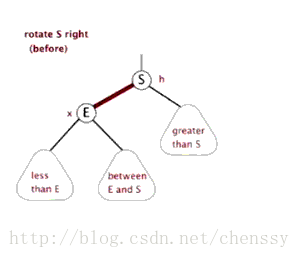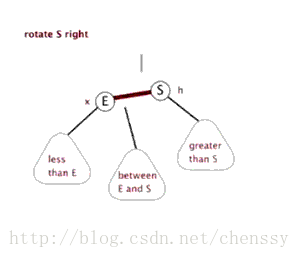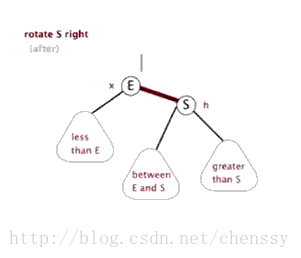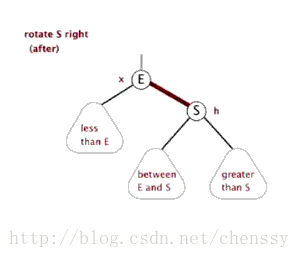
右旋:rotateRight()
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
//获取P的右子节点,其实这里就相当于新增节点N(情况四而言)
Entry<K,V> r = p.right;
//将R的左子树设置为P的右子树
p.right = r.left;
//若R的左子树不为空,则将P设置为R左子树的父亲
if (r.left != null)
r.left.parent = p;
//将P的父亲设置R的父亲
r.parent = p.parent;
//如果P的父亲为空,则将R设置为跟节点
if (p.parent == null)
root = r;
//如果P为其父节点(G)的左子树,则将R设置为P父节点(G)左子树
else if (p.parent.left == p)
p.parent.left = r;
//否则R设置为P的父节点(G)的右子树
else
p.parent.right = r;
//将P设置为R的左子树
r.left = p;
//将R设置为P的父节点
p.parent = r;
}
}所谓右旋转即,P.right ---> G、G.parent ---> P。
private void rotateRight(Entry<K,V> p) {
if (p != null) {
//将L设置为P的左子树
Entry<K,V> l = p.left;
//将L的右子树设置为P的左子树
p.left = l.right;
//若L的右子树不为空,则将P设置L的右子树的父节点
if (l.right != null)
l.right.parent = p;
//将P的父节点设置为L的父节点
l.parent = p.parent;
//如果P的父节点为空,则将L设置根节点
if (p.parent == null)
root = l;
//若P为其父节点的右子树,则将L设置为P的父节点的右子树
else if (p.parent.right == p)
p.parent.right = l;
//否则将L设置为P的父节点的左子树
else
p.parent.left = l;
//将P设置为L的右子树
l.right = p;
//将L设置为P的父节点
p.parent = l;
}
}左旋、右旋的示意图如下:

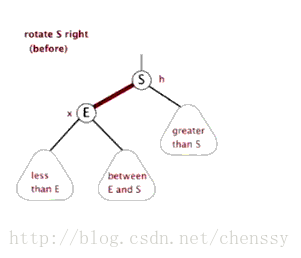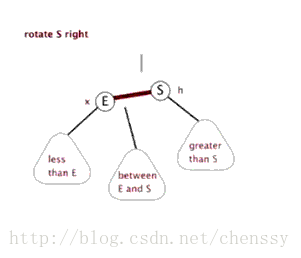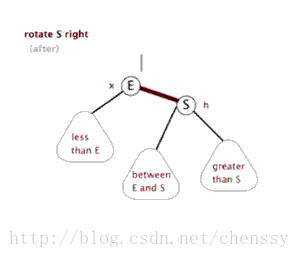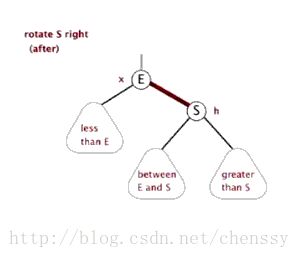
(左旋) (右旋)
(图片来自:http://www.php.cn/)
着色:setColor()
着色就是改变该节点的颜色,在红黑树中,它是依靠节点的颜色来维持平衡的。
private static <K,V> void setColor(Entry<K,V> p, boolean c) {
if (p != null)
p.color = c;
}针对于红黑树的增加节点而言,删除显得更加复杂,使原本就复杂的红黑树变得更加复杂。同时删除节点和增加节点一样,同样是找到删除的节点,删除之后调整红黑树。但是这里的删除节点并不是直接删除,而是通过走了“弯路”通过一种捷径来删除的:找到被删除的节点D的子节点C,用C来替代D,不是直接删除D,因为D被C替代了,直接删除C即可。所以这里就将删除父节点D的事情转变为了删除子节点C的事情,这样处理就将复杂的删除事件简单化了。子节点C的规则是:右分支最左边,或者 左分支最右边的。
红-黑二叉树删除节点,最大的麻烦是要保持 各分支黑色节点数目相等。 因为是删除,所以不用担心存在颜色冲突问题——插入才会引起颜色冲突。
红黑树删除节点同样会分成几种情况,这里是按照待删除节点有几个儿子的情况来进行分类:
1、没有儿子,即为叶结点。直接把父结点的对应儿子指针设为NULL,删除儿子结点就OK了。
2、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。
3、有两个儿子。这种情况比较复杂,但还是比较简单。上面提到过用子节点C替代代替待删除节点D,然后删除子节点C即可。
下面就论各种删除情况来进行图例讲解,但是在讲解之前请允许我再次啰嗦一句,请时刻牢记红黑树的5点规定:
1、每個節點只能是紅色或黑色
根節點是黑色3、每個葉節點(NIL節點,空節點)是黑色的。
4、如果一個結點是紅的,則它兩個子節點都是黑的。也就是說一條路徑上不能出現相鄰的兩個紅色結點。
5、從任何節點到其每個葉子的所有路徑都包含相同數目的黑色節點。
(註:已經講三遍了,再不記得我就是否適合做IT了O(_⎜)
誠然,既然刪除節點比較複雜,那麼在這裡我們就約定規則:
1、N要刪除,如前面提到的C。
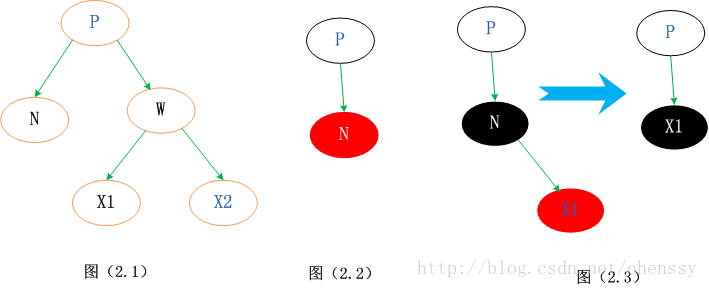
2、下面提到的刪除節點的樹都是如下結構,該結構左邊選取的節點是待刪除節點的右樹的最下方提到的刪除節點的樹都是如下結構,該結構的左邊選取節點是待刪除節點的右樹的最子節點。這裡我們規定真實刪除節點為N、父節點為P、兄弟節點為W兄弟節點的兩個子節點為X1、X2。如下圖(2.1)。
的三種情況進行分析、處理。
情況一、無子節點(紅色節點)
情況二、有一個子節點情況處理也是非常簡單的,用子節點取代待刪除節點,然後刪除子節點即可。如上圖(2.3)
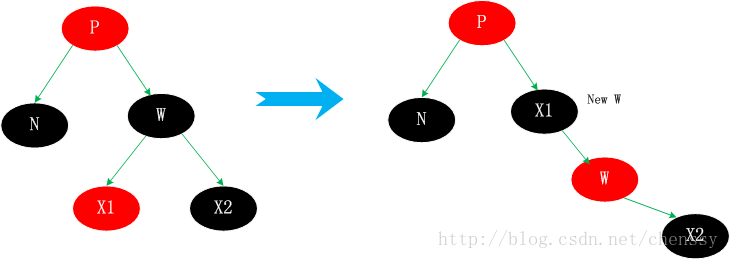
這種情況可能會稍微有點複雜。它需要找到一個替代待刪除節點(N)來取代它,然後刪除N即可。它主要分為四種情況。 1、N的兄弟節點W為紅色 孩子都是黑色的。 3、N的兄弟w是黑色的,w的左孩子是紅色,w的右孩子是黑色。 4、N的兄弟w是黑色的,且w的右孩子時紅色的。 情況3.1. W為紅色,那麼其子節點X1、X2必定全部為黑色,父節點P也為黑色。處理策略是:改變W、P的顏色,然後再進行一次左旋轉。這樣處理就可以使得紅黑性質得以繼續保持。 N的新兄弟new w是旋轉之前w的某個孩子,為黑色。這樣處理後將情況3.1、轉變為3.2、3.3、3.4中的一種。如下: 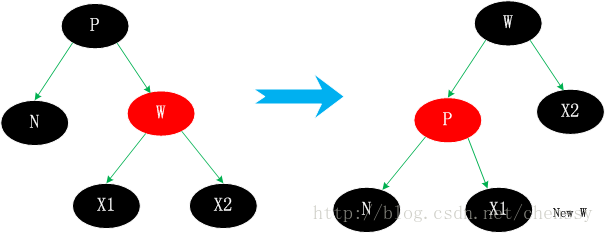
這種情況其父節點可紅可黑,由於W為W為,這樣導致一個外形樹可以將W置為紅色。這樣,N子樹與W子樹黑色節點一致,保持了平衡。以下
對於它的兄弟節點會少一個黑色節點。但如果new x為紅色,我們直接將new x轉變為黑色,保持整棵樹的平衡。否則情況3.2 會轉變為情況3.1、3.3、3.4中的一種。

針對這種情況是將節點與其左子節點進行右側色彩交換,然後對節點進行右側顏色旋轉。
情況3轉化為情況4.
总结 个人认为这四种情况比较难理解,首先他们都不是单一的某种情况,他们之间是可以进行互转的。相对于其他的几种情况,情况3.2比较好理解,仅仅只是一个颜色的转变,通过减少右子树的一个黑色节点使之保持平衡,同时将不平衡点上移至N与W的父节点,然后进行下一轮迭代。情况3.1,是将W旋转将其转成情况2、3、4情况进行处理。而情况3.3通过转变后可以化成情况3.4来进行处理,从这里可以看出情况3.4应该最终结。情况3.4、右子节点为红色节点,那么将缺失的黑色节点交由给右子节点,通过旋转达到平衡。 通过上面的分析,我们已经初步了解了红黑树的删除节点情况,相对于增加节点而言它确实是选的较为复杂。下面我将看到在Java TreeMap中是如何实现红黑树删除的。 通过上面的分析我们确认删除节点的步骤是:找到一个替代子节点C来替代P,然后直接删除C,最后调整这棵红黑树。下面代码是寻找替代节点、删除替代节点。 (1)除是寻找替代节点replacement,其实现方法为successor()。如下: (2)处是删除该节点过程。它主要分为上面提到的三种情况,它与上面的if…else if… else一一对应 。如下: 1、有两个儿子。这种情况比较复杂,但还是比较简单。上面提到过用子节点C替代代替待删除节点D,然后删除子节点C即可。 2、没有儿子,即为叶结点。直接把父结点的对应儿子指针设为NULL,删除儿子结点就OK了。 3、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。 删除完节点后,就要根据情况来对红黑树进行复杂的调整:fixAfterDeletion()。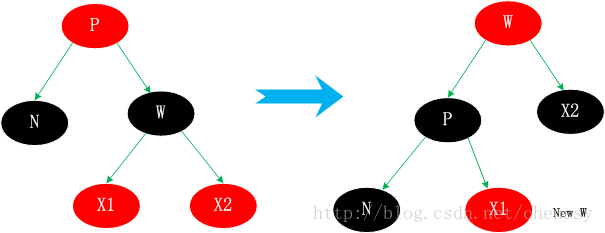
TreeMap deleteEntry()方法实现分析
private void deleteEntry(Entry<K,V> p) {
modCount++; //修改次数 +1
size--; //元素个数 -1
/*
* 被删除节点的左子树和右子树都不为空,那么就用 p节点的中序后继节点代替 p 节点
* successor(P)方法为寻找P的替代节点。规则是右分支最左边,或者 左分支最右边的节点
* ---------------------(1)
*/
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
}
//replacement为替代节点,如果P的左子树存在那么就用左子树替代,否则用右子树替代
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
/*
* 删除节点,分为上面提到的三种情况
* -----------------------(2)
*/
//如果替代节点不为空
if (replacement != null) {
replacement.parent = p.parent;
/*
*replacement来替代P节点
*/
//若P没有父节点,则跟节点直接变成replacement
if (p.parent == null)
root = replacement;
//如果P为左节点,则用replacement来替代为左节点
else if (p == p.parent.left)
p.parent.left = replacement;
//如果P为右节点,则用replacement来替代为右节点
else
p.parent.right = replacement;
//同时将P节点从这棵树中剔除掉
p.left = p.right = p.parent = null;
/*
* 若P为红色直接删除,红黑树保持平衡
* 但是若P为黑色,则需要调整红黑树使其保持平衡
*/
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { //p没有父节点,表示为P根节点,直接删除即可
root = null;
} else { //P节点不存在子节点,直接删除即可
if (p.color == BLACK) //如果P节点的颜色为黑色,对红黑树进行调整
fixAfterDeletion(p);
//删除P节点
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
/*
* 寻找右子树的最左子树
*/
else if (t.right != null) {
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
}
/*
* 选择左子树的最右子树
*/
else {
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}private void fixAfterDeletion(Entry<K,V> x) {
// 删除节点需要一直迭代,知道 直到 x 不是根节点,且 x 的颜色是黑色
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) { //若X节点为左节点
//获取其兄弟节点
Entry<K,V> sib = rightOf(parentOf(x));
/*
* 如果兄弟节点为红色----(情况3.1)
* 策略:改变W、P的颜色,然后进行一次左旋转
*/
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
/*
* 若兄弟节点的两个子节点都为黑色----(情况3.2)
* 策略:将兄弟节点编程红色
*/
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
}
else {
/*
* 如果兄弟节点只有右子树为黑色----(情况3.3)
* 策略:将兄弟节点与其左子树进行颜色互换然后进行右转
* 这时情况会转变为3.4
*/
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
/*
*----情况3.4
*策略:交换兄弟节点和父节点的颜色,
*同时将兄弟节点右子树设置为黑色,最后左旋转
*/
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
}
/**
* X节点为右节点与其为做节点处理过程差不多,这里就不在累述了
*/
else {
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
这是红黑树在删除节点后,对树的平衡性进行调整的过程,其实现过程与上面四种复杂的情况一一对应,所以在这个源码的时候一定要对着上面提到的四种情况看。
同時這篇博文我寫了四天,看了、參考了大量的博文。同時不免會有些地方存在藉鏡之處,在這裡對其表示感謝。 LZ大二開始學習資料結構,自認為學的不錯,現在發現資料結構我還有太多的地方要學習了,同時也再一次體味了演算法的魅力! ! !
以上就是Java提高篇(二七)-----TreeMap 的內容,更多相關內容請關注PHP中文網(www.php.cn)!




