學到遞歸的時候有個漢諾塔的練習,漢諾塔應該是學習電腦遞歸演算法的經典入門案例了,所以本人覺得可以寫篇博客來表達一下自己的見解。這markdown編輯器還不怎麼會用,可能寫的有點格式有點醜啦,各位看官多多見諒.
網上找了一張漢諾塔的圖片,漢諾塔就是利用用中間的柱子把最左邊的柱子上的圓盤依序從大到小疊上去,說白了就是c要跟原來的a一樣

#廢話少說,先亮程式碼
def move(n, a, buffer, c):
if(n == 1):
print(a,"->",c)
return
move(n-1, a, c, buffer)
move(1, a, buffer, c)
move(n-1, buffer, a, c)
move(3, "a", "b", "c") 首先是定義了一個移動的函數,四個參數分別代表,a柱上的盤子個數,buffer也就是b柱,命名為buffer便於理解,顧名思義就是一個a移動到c的緩衝區.然後c就是目標柱子
下面我們來讀函數代碼
遞歸的一般寫法,肯定有個中止遞歸循環的條件,所以在判斷a柱上的盤子個數為1的時候既可以中止遞歸並返回,a柱上面只有一個的時候肯定就是把a移動到c了,重點是下面的代碼,遞歸其實是很抽象的演算法,我們要利用抽象思考去想漢諾塔這個問題,把a柱上的盤子想成兩份,就是上面的盤子和最底下的盤子,如果所示
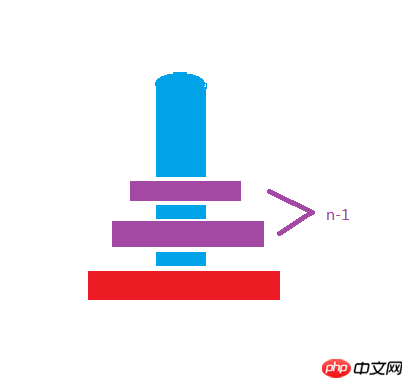
# 我們不關心上面的盤子到底有幾個,我們每次的操作就是把最底下的盤子通過緩衝區b柱buffer 移動到c柱。
童鞋們肯定在想為啥要醬紫移動呢,其實這是一種總結歸納吧,你自己玩一下漢諾塔遊戲就會發現規律,其實這個遊戲就是不停的把上面的所有的想方設法的移到b上,然後把a最後最大的那個弄到c,然後再絞盡腦汁的把b上的移動到c,這時候你就發現,原來b上的也要先通過空的也就是a來存放當前b上面的n-1個,然後把b的最大最後的移動到c,這裡規律就體現出來了,也可以抽像出移動的方法,並可以以此設計出程式演算法.
以下我們來利用剛才的抽象思考來解讀剩餘程式碼
##move(n-1, a, c, buffer)
這段程式碼就是表示把剛才所說的a柱的上面的n-1個,通過c按照從小到大的規則先移動到緩衝區buffer。此函數進入遞歸。move(1, a, buffer, c)
當上面的語句執行完成,也就是n-1個盤子的遞歸移動完成之後,執行此語句,就是把a柱上的一個盤子移到c,也就是所謂的最底下的盤子move(n-1, buffer , a, c)
最後一步,就是剛才把a上面的n-1個都移動到了buffer上面,肯定要通過a移動到c才能完成整個漢諾塔的移動啊,於是最後一步自然是把剛才的n-1個透過a當緩衝區移動到c柱上. 我來寫下整個移動流程,以a柱上有3個為例子
/**
我把3个盘子的汉诺塔全部通过代码演示,按缩进原则,每一个缩进即进一个递归函数,每打印一次即中止当前递归,也就是每个print
说明:
1.n = 3, n = 2, n = 1是每次执行if(n == 1)的结果,这里就不写判断了,相信童鞋们也能看懂,也就是n不等与1时就减1进入递归
2.请注意a,b,c柱每次进入函数的顺序,不要被形参带错路了,看准每次函数参数的实参
**/
move(3, "a", "b", "c")
n=3:
//开始从a上移动n-1即2个盘子通过c移动到b,以腾出c供a最后一个盘子移动
move(2, "a","c","b")
n=2:
//开始进行n=2的一个递归,把当前a('a')柱上的n-1个盘子通过c('b')移动到b('c')
move(1, "a", "b", "c")
n=1:
//n=2的第一个递归完成,打印结果,执行当前子函数剩余代码
print("a", "->", "c")
move(1, "a", "c", "b")
n=1:
print("a", "->", "b")
move(1, "c", "a", "b")
n=1:
print("c", "->", "b")
//到这里完成了a柱上面的n-1即是2个盘子的移动
//开始把a柱上最后一个盘子移动到c柱上
move(1, "a", "b", "c")
n=1:
print("a", "->", "c")
//到这里完成移动a柱上的最后一个盘子到c柱上
move(2, "b", "a", "c")
n=2:
//开始进行n=2的第二个递归,即把当前b('b')的盘子(n-1个)通过a('a')移动到c('c')上
move(1, "b", "c", "a")
n=1:
//n=2 的第二个递归完成,打印结果并执行当前子函数的剩余代码
print("b", "->", "a")
move(1, "b", "a", "c")
n=1:
print("b", "->", "c")
move(1, "a", "b", "c")
n=1:
print("a", "->", "c")
//到这里把b上的盘子通过a移动到c,
//整个代码执行完毕,汉诺塔移动完成




