Python實作二元堆的方法
二元堆是一種特殊的堆,二元堆是完全二元樹(二元樹)或近似完全二元樹(二元樹)。二元堆有兩種:最大堆和最小堆。最大堆:父結點的鍵值總是大於或等於任何一個子節點的鍵值;最小堆:父結點的鍵值總是小於或等於任何一個子節點的鍵值。
優先佇列的二元堆實作
在前面的章節裡我們學習了「先進先出」(FIFO)的資料結構:隊列(Queue)。隊列有一種變體叫做「優先隊列」(Priority Queue)。優先隊列的出隊(Dequeue)操作和隊列一樣,都是從隊首出隊。但在優先隊列的內部,元素的次序是由「優先」來決定:高優先級的元素排在隊首,而低優先級的元素則排在後面。這樣,優先隊列的入隊(Enqueue)操作就比較複雜,需要將元素依照優先權盡量排到佇列前面。我們將會發現,對於下一節要學的圖演算法中的優先隊列是很有用的資料結構。
我們很自然地會想到用排序演算法和佇列的方法來實作優先隊列。但是,在列表裡插入一個元素的時間複雜度是O(n),對列表進行排序的時間複雜度是O(nlogn)。我們可以用別的方法來降低時間複雜度。一個實現優先隊列的經典方法就是採用二元堆(Binary Heap)。二元堆能將優先隊列的入隊和出隊複雜度都保持在O(logn)。
二元堆的有趣之處在於,其邏輯結構上像二元樹,卻是用非嵌套的列表來實現。二元堆有兩種:鍵值總是最小的排在隊首稱為“最小堆(min heap)”,反之,鍵值總是最大的排在隊首稱為“最大堆(max heap)」。在這一節裡我們使用最小堆。
二元堆的操作
二元堆的基本運算定義如下:
BinaryHeap():建立一個空的二元堆物件insert(k):將新元素加入堆中-
#findMin():傳回堆中的最小項,最小項仍保留在堆中 ##delMin()
:傳回堆中的最小項,同時從堆中刪除isEmpty()
:傳回堆是否為空size()
:傳回堆中節點的個數#buildHeap(list)
:從一個包含節點的清單建立新堆
from pythonds.trees.binheap import BinHeap bh = BinHeap() bh.insert(5) bh.insert(7) bh.insert(3) bh.insert(11) print(bh.delMin()) print(bh.delMin()) print(bh.delMin()) print(bh.delMin())

n,那麼父節點下標為n//2.圖 2 所示是一個完全二元樹和樹的列表表示法。注意父節點與子節點之間 2p 與 2p+1 的關係。完全樹的列表表示法結合了完全二元樹的特性,使我們能夠使用簡單的數學方法有效地遍歷一棵完全樹。這也使我們能高效實現二元堆。
堆次序的性質
我們在堆裡儲存元素的方法依賴堆的次序。所謂堆次序,是指堆中任何一個節點 x,其父節點 p 的鍵值均小於或等於 x 的鍵值。圖 2 所示是具備堆次序性質的完全二元樹。
#二元堆疊運算的實作#
接下来我们来构造二叉堆。因为可以采用一个列表保存堆的数据,构造函数只需要初始化一个列表和一个currentSize来表示堆当前的大小。Listing 1 所示的是构造二叉堆的 python 代码。注意到二叉堆的heaplist并没有用到,但为了后面代码可以方便地使用整除,我们仍然保留它。
Listing 1
class BinHeap:
def init(self):
self.heapList = [0]
self.currentSize = 0我们接下来要实现的是insert方法。首先,为了满足“完全二叉树”的性质,新键值应该添加到列表的末尾。然而新键值简单地添加在列表末尾,显然无法满足堆次序。但我们可以通过比较父节点和新加入的元素的方法来重新满足堆次序。如果新加入的元素比父节点要小,可以与父节点互换位置。图 3 所示的是一系列交换操作来使新加入元素“上浮”到正确的位置。

图 3:新节点“上浮”到其正确位置
当我们让一个元素“上浮”时,我们要保证新节点与父节点以及其他兄弟节点之间的堆次序。当然,如果新节点非常小,我们仍然需要将它交换到其他层。事实上,我们需要不断交换,直到到达树的顶端。Listing 2 所示的是“上浮”方法,它把一个新节点“上浮”到其正确位置来满足堆次序。这里很好地体现了我们之前在headlist中没有用到的元素 0 的重要性。这样只需要做简单的整除,将当前节点的下标除以 2,我们就能计算出任何节点的父节点。
在Listing 3 中,我们已经可以写出insert方法的代码。insert里面很大一部分工作是由percUp函数完成的。当树添加新节点时,调用percUp就可以将新节点放到正确的位置上。
Listing 2
def percUp(self,i):
while i // 2 > 0:
if self.heapList[i] < self.heapList[i // 2]:
tmp = self.heapList[i // 2]
self.heapList[i // 2] = self.heapList[i]
self.heapList[i] = tmp
i = i // 2Listing 3
def insert(self,k): self.heapList.append(k) self.currentSize = self.currentSize + 1 self.percUp(self.currentSize)
我们已经写好了insert方法,那再来看看delMin方法。堆次序要求根节点是树中最小的元素,因此很容易找到最小项。比较困难的是移走根节点的元素后如何保持堆结构和堆次序,我们可以分两步走。首先,用最后一个节点来代替根节点。移走最后一个节点保持了堆结构的性质。这么简单的替换,还是会破坏堆次序。那么第二步,将新节点“下沉”来恢复堆次序。图 4 所示的是一系列交换操作来使新节点“下沉”到正确的位置。

图 4:替换后的根节点下沉
为了保持堆次序,我们需将新的根节点沿着一条路径“下沉”,直到比两个子节点都小。在选择下沉路径时,如果新根节点比子节点大,那么选择较小的子节点与之交换。Listing 4 所示的是新节点下沉所需的percDown和minChild方法的代码。
Listing 4
def percDown(self,i):
while (i * 2) <= self.currentSize:
mc = self.minChild(i)
if self.heapList[i] > self.heapList[mc]:
tmp = self.heapList[i]
self.heapList[i] = self.heapList[mc]
self.heapList[mc] = tmp
i = mc
def minChild(self,i):
if i * 2 + 1 > self.currentSize:
return i * 2
else:
if self.heapList[i*2] < self.heapList[i*2+1]:
return i * 2
else:
return i * 2 + 1Listing 5 所示的是delMin操作的代码。可以看到比较麻烦的地方由一个辅助函数来处理,即percDown。
Listing 5
def delMin(self): retval = self.heapList[1] self.heapList[1] = self.heapList[self.currentSize] self.currentSize = self.currentSize - 1 self.heapList.pop() self.percDown(1) return retval
关于二叉堆的最后一部分便是找到从无序列表生成一个“堆”的方法。我们首先想到的是,将无序列表中的每个元素依次插入到堆中。对于一个排好序的列表,我们可以用二分搜索找到合适的位置,然后在下一个位置插入这个键值到堆中,时间复杂度为O(logn)。另外插入一个元素到列表中需要将列表的一些其他元素移动,为新节点腾出位置,时间复杂度为O(n)。因此用insert方法的总开销是O(nlogn)。其实我们能直接将整个列表生成堆,将总开销控制在O(n)。Listing 6 所示的是生成堆的操作。
Listing 6
def buildHeap(self,alist):
i = len(alist) // 2
self.currentSize = len(alist)
self.heapList = [0] + alist[:]
while (i > 0):
self.percDown(i)
i = i - 1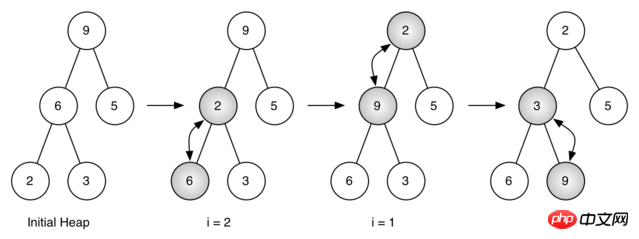
图 5:将列表[ 9, 6, 5, 2, 3]生成一个二叉堆
图 5 所示的是利用buildHeap方法将最开始的树[ 9, 6, 5, 2, 3]中的节点移动到正确的位置时所做的交换操作。尽管我们从树中间开始,然后回溯到根节点,但percDown方法保证了最大子节点总是“下沉”。因为堆是完全二叉树,任何在中间的节点都是叶节点,因此没有子节点。注意,当i=1时,我们从根节点开始下沉,这就需要进行大量的交换操作。可以看到,图 5 最右边的两颗树,首先 9 从根节点的位置移走,移到下一层级之后,percDown进一步检查它此时的子节点,保证它下降到不能再下降为止,即下降到正确的位置。然后进行第二次交换,9 和 3 的交换。由于 9 已经移到了树最底层的层级,便无法进一步交换了。比较一下列表表示法和图 5 所示的树表示法进行的一系列交换还是很有帮助的。
i = 2 [0, 9, 5, 6, 2, 3] i = 1 [0, 9, 2, 6, 5, 3] i = 0 [0, 2, 3, 6, 5, 9]
下列所示的代码是完全二叉堆的实现。
def insert(self,k):
self.heapList.append(k)
self.currentSize = self.currentSize + 1
self.percUp(self.currentSize)
def percDown(self,i):
while (i * 2) <= self.currentSize:
mc = self.minChild(i)
if self.heapList[i] > self.heapList[mc]:
tmp = self.heapList[i]
self.heapList[i] = self.heapList[mc]
self.heapList[mc] = tmp
i = mc
def minChild(self,i):
if i * 2 + 1 > self.currentSize:
return i * 2
else:
if self.heapList[i*2] < self.heapList[i*2+1]:
return i * 2
else:
return i * 2 + 1
def delMin(self):
retval = self.heapList[1]
self.heapList[1] = self.heapList[self.currentSize]
self.currentSize = self.currentSize - 1能在O(n)的开销下能生成二叉堆看起来有点不可思议,其证明超出了本书的范围。但是,要理解用O(n)的开销能生成堆的关键是因为logn因子基于树的高度。而对于buildHeap里的许多操作,树的高度比logn要小。
以上是Python實作二元堆的方法的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 PHP和Python:解釋了不同的範例
Apr 18, 2025 am 12:26 AM
PHP和Python:解釋了不同的範例
Apr 18, 2025 am 12:26 AM
PHP主要是過程式編程,但也支持面向對象編程(OOP);Python支持多種範式,包括OOP、函數式和過程式編程。 PHP適合web開發,Python適用於多種應用,如數據分析和機器學習。
 在PHP和Python之間進行選擇:指南
Apr 18, 2025 am 12:24 AM
在PHP和Python之間進行選擇:指南
Apr 18, 2025 am 12:24 AM
PHP適合網頁開發和快速原型開發,Python適用於數據科學和機器學習。 1.PHP用於動態網頁開發,語法簡單,適合快速開發。 2.Python語法簡潔,適用於多領域,庫生態系統強大。
 sublime怎麼運行代碼python
Apr 16, 2025 am 08:48 AM
sublime怎麼運行代碼python
Apr 16, 2025 am 08:48 AM
在 Sublime Text 中運行 Python 代碼,需先安裝 Python 插件,再創建 .py 文件並編寫代碼,最後按 Ctrl B 運行代碼,輸出會在控制台中顯示。
 PHP和Python:深入了解他們的歷史
Apr 18, 2025 am 12:25 AM
PHP和Python:深入了解他們的歷史
Apr 18, 2025 am 12:25 AM
PHP起源於1994年,由RasmusLerdorf開發,最初用於跟踪網站訪問者,逐漸演變為服務器端腳本語言,廣泛應用於網頁開發。 Python由GuidovanRossum於1980年代末開發,1991年首次發布,強調代碼可讀性和簡潔性,適用於科學計算、數據分析等領域。
 Python vs. JavaScript:學習曲線和易用性
Apr 16, 2025 am 12:12 AM
Python vs. JavaScript:學習曲線和易用性
Apr 16, 2025 am 12:12 AM
Python更適合初學者,學習曲線平緩,語法簡潔;JavaScript適合前端開發,學習曲線較陡,語法靈活。 1.Python語法直觀,適用於數據科學和後端開發。 2.JavaScript靈活,廣泛用於前端和服務器端編程。
 Golang vs. Python:性能和可伸縮性
Apr 19, 2025 am 12:18 AM
Golang vs. Python:性能和可伸縮性
Apr 19, 2025 am 12:18 AM
Golang在性能和可擴展性方面優於Python。 1)Golang的編譯型特性和高效並發模型使其在高並發場景下表現出色。 2)Python作為解釋型語言,執行速度較慢,但通過工具如Cython可優化性能。
 vscode在哪寫代碼
Apr 15, 2025 pm 09:54 PM
vscode在哪寫代碼
Apr 15, 2025 pm 09:54 PM
在 Visual Studio Code(VSCode)中編寫代碼簡單易行,只需安裝 VSCode、創建項目、選擇語言、創建文件、編寫代碼、保存並運行即可。 VSCode 的優點包括跨平台、免費開源、強大功能、擴展豐富,以及輕量快速。
 notepad 怎麼運行python
Apr 16, 2025 pm 07:33 PM
notepad 怎麼運行python
Apr 16, 2025 pm 07:33 PM
在 Notepad 中運行 Python 代碼需要安裝 Python 可執行文件和 NppExec 插件。安裝 Python 並為其添加 PATH 後,在 NppExec 插件中配置命令為“python”、參數為“{CURRENT_DIRECTORY}{FILE_NAME}”,即可在 Notepad 中通過快捷鍵“F6”運行 Python 代碼。






