Python實作二元搜尋樹的方法-Python教學-PHP中文網

二元搜尋樹(二元排序樹)它的每個節點的資料結構為1個父節點指標,1個左孩子指標,1個有孩子指標,還有就是自己的數據部分了,因為只有左右兩孩子,所以才叫二叉樹,在此基礎上,該二叉樹還滿足另外一個條件:每個結點的左孩子都不大於該結點&&每個結點的右孩子都大於該結點.

二叉搜尋樹

#我們已經知道了在一個集合中獲取鍵值對的兩種不同的方法。回想一下這些集合是如何實作ADT（抽象資料型別）MAP的。我們討論兩種ADT MAP的實作方式，基於列表的二分查找和雜湊表。在這一節中，我們將要學習二元搜尋樹，這是另一個鍵指向值的Map集合，在這種情況下我們不用考慮元素在樹中的實際位置，但要知道使用二元樹來搜尋更有效率。

搜尋樹運算

在我們研究這個實作方式之前，讓我們先回顧一下ADT MAP提供的介面#。我們會注意到，這種介面和Python的字典非常相似。

Map() 建立了一個新的空白Map集合。
put(key,val) 在Map中增加了一個新的鍵值對。如果這個鍵已經在這個Map中了，那麼就用新的值來取代舊的值。
get(key) 提供一個鍵，傳回Map中儲存的數據，或傳回None。
del 使用del map[key]這條語句從Map中刪除鍵值對。
len() 傳回Map中儲存的鍵值對的數目
in 如果所給的鍵在Map中，使用key in map這語句傳回True。

搜尋樹實作

一個二元搜尋樹，如果具有左子樹中的鍵值都小於父節點，而右子樹中的鍵值都大於父節點的屬性，我們將這種樹稱為BST搜尋樹。如之前所述的，當我們實作Map時，BST方法將引導我們實現這一點。圖 1 展示了二元搜尋樹的這項特性，顯示的鍵沒有關聯任何的值。注意這種屬性適用於每個父節點和子節點。所有在左子樹的鍵值都小於根節點的鍵值，所有右子樹的鍵值都大於根節點的鍵值。

Python實作二元搜尋樹的方法

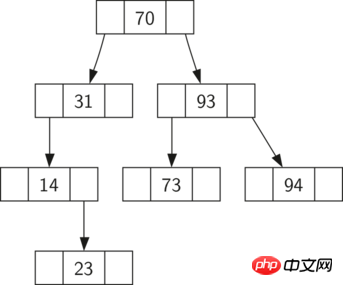
圖1：一個簡單的二元搜尋樹

現在你知道什麼是二元搜尋樹了，我們再來看如何建構一個二元搜尋樹，我們在搜尋樹中按圖1 顯示的節點順序插入這些鍵值，圖1 搜尋樹存在的節點：70,31,93,94,14,23,73。因為 70 是第一個被插入到樹的值，它是根節點。接下來，31 小於 70，因此是 70 的左子樹。接下來，93 大於 70，因此是 70 的右子樹。我們現在填滿了該樹的兩層，所以下一個鍵值，將會是 31 或 93 的左子樹或右子樹。由於 94 大於 70 和 93，就變成了 93 的右子樹。同樣，14 小於 70 和 31，因此成為了 31 的左子樹。 23 也小於 31，因此必須是 31 的左子樹。然而，它大於 14，所以是 14 的右子樹。

為了實作二元搜尋樹，我們將使用節點和引用的方法，這類似於我們實作鍊錶和表達式樹的過程。因為我們必須能夠創建和使用一個空的二元搜尋樹，所以我們將使用兩個類別來實現，第一個類別我們稱之為 BinarySearchTree，第二個類別我們稱之為TreeNode。 BinarySearchTree類別有一個TreeNode類別的引用作為二元搜尋樹的根，在大多數情況下，外部類別定義的外部方法只需檢查樹是否為空，如果在樹上有節點，要求BinarySearchTree類別中含有私有方法把根定義為參數。在這種情況下，如果樹是空的或我們想刪除樹的根，我們必須採取特殊操作。 BinarySearchTree類別的建構子以及一些其他函式的程式碼如Listing 1 所示。

Listing 1

class BinarySearchTree:

  def init(self):
    self.root = None
    self.size = 0

  def length(self):
    return self.size

  def len(self):
    return self.size

  def iter(self):
    return self.root.iter()

登入後複製

TreeNode類別提供了許多輔助函數，使得BinarySearchTree類別的方法更容易實作過程。如Listing 2 所示，一個樹節點的結構，是由這些輔助函數實現的。正如你看到的那樣，這些輔助函數可以根據自己的位置來劃分一個節點作為左或右孩子和該子節點的類型。 TreeNode類別非常清楚地追蹤了每個父節點的屬性。當我們討論刪除操作的實作時，你將明白為什麼這很重要。

對於Listing 2 中的TreeNode實現，另一個有趣的地方是，我們使用Python的可選參數。可選的參數很容易讓我們在幾種不同的情況下建立一個樹節點，有時我們想建立一個新的樹節點，即使我們已經有了父節點和子節點。與現有的父節點和子節點一樣，我們可以透過父節點和子節點作為參數。有時我們也會建立一個包含鍵值對的樹，我們不會傳遞父節點或子節點的任何參數。在這種情況下，我們將使用可選參數的預設值。

Listing 2

class TreeNode:
  def init(self,key,val,left=None,right=None,
                    parent=None):
    self.key = key
    self.payload = val
    self.leftChild = left
    self.rightChild = right
    self.parent = parent

  def hasLeftChild(self):
    return self.leftChild

  def hasRightChild(self):
    return self.rightChild

  def isLeftChild(self):
    return self.parent and self.parent.leftChild == self

  def isRightChild(self):
    return self.parent and self.parent.rightChild == self

  def isRoot(self):
    return not self.parent

  def isLeaf(self):
    return not (self.rightChild or self.leftChild)

  def hasAnyChildren(self):
    return self.rightChild or self.leftChild

  def hasBothChildren(self):
    return self.rightChild and self.leftChild

  def replaceNodeData(self,key,value,lc,rc):
    self.key = key
    self.payload = value
    self.leftChild = lc
    self.rightChild = rc
    if self.hasLeftChild():
      self.leftChild.parent = self
    if self.hasRightChild():
      self.rightChild.parent = self

登入後複製

現在，我們擁有了BinarySearchTree和TreeNode類，是時候寫一個put方法使我們能夠建立一個二元搜尋樹。 put方法是BinarySearchTree類別的一個方法。這個方法將檢查這棵樹是否已經有根。如果沒有，我們將創建一個新的樹節點並把它設定為樹的根。如果已經有一個根節點，我們就呼叫它自己，進行遞歸，用輔助函數_put按下列演算法來搜尋樹：

從樹的根節點開始，透過搜尋二元樹來比較新的鍵值和目前節點的鍵值，如果新的鍵值小於目前節點，則搜尋左子樹。如果新的關鍵大於目前節點，則搜尋右子樹。

當搜尋不到左（或右）子樹，我們在樹中所處的位置就是設定新節點的位置。
在樹中新增一個節點，建立一個新的TreeNode物件並在這個點的上一個節點中插入這個物件。

Listing 3 顯示了在樹中插入新節點的Python程式碼。 _put函數要依照上述的步驟來寫遞歸演算法。請注意，當一個新的子樹插入時，當前節點（CurrentNode）會作為父節點傳遞給新的樹。

我們執行插入的一個重要問題是重複的鍵值不能被正確的處理，我們的樹實現了鍵值的複製，它將在右子樹創建一個與原來節點鍵值相同的新節點。這樣做的後果是，新的節點將不會在搜尋過程中被發現。我們用一個更好的方式來處理插入重複的鍵值，舊的值被新鍵關聯的值取代。我們把這個錯誤的修復，當作練習留給你。

Listing 3

def put(self,key,val):
  if self.root:
    self._put(key,val,self.root)
  else:
    self.root = TreeNode(key,val)
  self.size = self.size + 1

def _put(self,key,val,currentNode):
  if key < currentNode.key:
    if currentNode.hasLeftChild():
        self._put(key,val,currentNode.leftChild)
    else:
        currentNode.leftChild = TreeNode(key,val,parent=currentNode)
  else:
    if currentNode.hasRightChild():
        self._put(key,val,currentNode.rightChild)
    else:
        currentNode.rightChild = TreeNode(key,val,parent=currentNode)

登入後複製

隨著put方法的實現，我們可以很容易地透過setitem方法重載[]作為運算子來呼叫put方法（參見Listing 4）。這使我們能夠編寫像myZipTree['Plymouth'] = 55446一樣的python語句，這看起來就像Python的字典。

Listing 4

def setitem(self,k,v):
  self.put(k,v)

登入後複製

圖 2 說明了將新節點插入到一個二元搜尋樹的過程。灰色節點顯示了插入過程中遍歷樹節點順序。

Python實作二元搜尋樹的方法

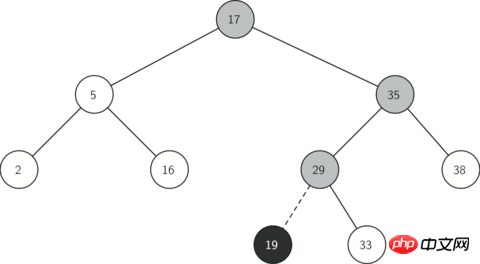
圖2: 插入一個鍵值= 19 的節點

一旦樹被構造，接下來的任務就是為一個給定的鍵值實現檢索。 get方法比put方法更容易因為它只需要遞歸搜尋樹，直到發現不匹配的葉節點或找到一個匹配的鍵值。當找到一個符合的鍵值後，就會傳回節點中的值。

Listing 5 顯示了get，_get和getitem的程式碼。用_get方法搜尋的程式碼與put方法具有相同的選擇左或右子樹的邏輯。請注意，_get方法傳回TreeNode中get的值，_get就可以作為一個靈活有效的方式，為BinarySearchTree的其他可能需要使用TreeNode裡的資料的方法提供參數。

透過實作getitem方法，我們可以寫一個看起來就像我們存取字典一樣的Python語句，而事實上我們只是操作二元搜尋樹，例如Z = myziptree ['fargo']。正如你所看到的，getitem方法都是在呼叫get。

Listing 5

def get(self,key):
  if self.root:
    res = self._get(key,self.root)
    if res:
        return res.payload
    else:
        return None
  else:
    return None

def _get(self,key,currentNode):
  if not currentNode:
    return None
  elif currentNode.key == key:
    return currentNode
  elif key < currentNode.key:
    return self._get(key,currentNode.leftChild)
  else:
    return self._get(key,currentNode.rightChild)

def getitem(self,key):
  return self.get(key)

登入後複製

使用get，我们可以通过写一个BinarySearchTree的contains方法来实现操作，contains方法简单地调用了get方法，如果它有返回值就返回True，如果它是None就返回False。如Listing 6 所示。

Listing 6

def contains(self,key):
  if self._get(key,self.root):
    return True
  else:
    return False

登入後複製

回顾一下contains重载的操作符，这允许我们写这样的语句：

if &#39;Northfield&#39; in myZipTree:
  print("oom ya ya")

登入後複製

以上是Python實作二元搜尋樹的方法的詳細內容。更多資訊請關注PHP中文網其他相關文章！