
內文:
拼圖是一個非常經典的遊戲,基本上每個人都知道他的玩法,他的開始,運行,結束。那麼,當我們想要做拼圖的時候該如何入手呢?答案是:從現實出發,去描述需求(盡量描述為文件),當我們擁有了全面的需求,就能夠提供可靠的策略,從而在程式碼中實現,最終成為作品!
(一)需求:(這個需求書寫較為潦草,為廣大小白定制,按照最最普通人的思維來,按照參與遊戲的流程來)
1.圖片:我們玩拼圖最起碼有個圖
2.切割:拼圖不是一個圖,我們需要把一個整圖它切割成N*N的小圖
3.打亂:把這N*N的小圖打亂順序,但是要保證透過遊戲規則行走能還原回來
4.判斷:判拼圖成功
5.互動:我們使用哪一種互動方式,這裡我選擇滑鼠點選
6.展示原始圖片完整的縮圖
## 以上為基本功能,以下為擴充功能 7.記錄步數:記錄完成需要多少步驟 8.更換圖片:一個圖片玩久了我們是不是可以換一換啊哈哈 9.選擇難度:太簡單?不要! 3*3搞定了有5*5,5*5搞定了有9*9,舍友挑戰最高難度(二)分析:
有了需求,我們就可以分析如何去實現它(把現實需求映射在計算機中),其中包括: 1.開發平台:這裡選擇C#語言 1.儲存:其中包括我們要存什麼?我們用什麼結構存?我們反觀需求,會發現,有一些需要儲存的資源 圖片:使用Image # 子單元(原始圖片切割後的圖片集合定義結構體 struct Node ,其中包括Image物件用來儲存單元小圖片,和用整形儲存的編號(切割以後,每個小單元都弄個編號,利於檢驗遊戲是否完成)。
各單元(原圖片切割後的子圖像集合):使用二維數組(像拼圖,五子棋,消消樂,連連看,俄羅斯方塊等平面點陣遊戲都可以用他來存儲,為什麼? 變數
int Num存儲 有了存儲,我們就可以去思考模組的劃分(正確的邏輯劃分已於擴展,也可以使通信變得更加清晰)並搭建,並實現各模組所涉及的特定演算法
首先程式的模組分為四個:邏輯型:
# 1.拼圖類別:用於描述拼圖2.配置類別:儲存設定變數
互動型:
##讓遊戲選單視窗:3.遊戲選單視窗:
3.遊戲選單視窗: 3.遊戲選單視窗:進行選單選項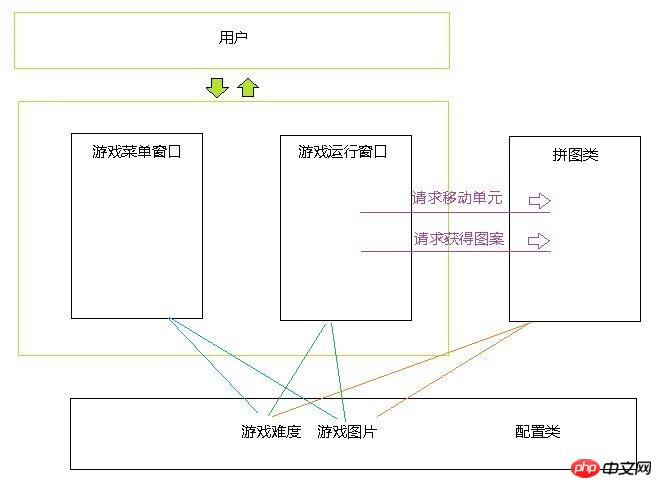
1.透過遊戲選單可以操縱配置,如遊戲選單可以操縱配置,如遊戲選單可以操縱配置,如遊戲選單可以操縱配置難度或圖片。
2.運行視窗可以存取並獲得遊戲配置,並利用其對應建構拼圖物件。 3.用戶透過運行視窗進行交互,間接使拼圖物件調用移動方法,獲得圖案方法
看程式碼的同學,我覺得最有問題的地方,不合理的地方就是把難度的枚舉型別寫在了拼圖類別中,應該寫在配置類別中,或單獨成類,讀者們自行更改
public enum Diff //游戏难度 {
simple,//简单
ordinary,//普通
difficulty//困难
}我们可以认为,配置类就像数据存储,而拼图类呢作为逻辑处理,菜单和运行窗口作为表现用于交互,我承认这种设计不是很合理,但是在问题规模不够大的时候,过分的考虑设计,会不会使程序变得臃肿?我想一定是有一个度,具体是多少,我不得而知,但我感觉,针对这个程序,实现就好,沉迷设计(套路型),有时得不偿失。(个人不成熟的小观点)
(三)代码实现:
说明:本块重点描述 Puzzle(拼图)类与游戏运行类的具体实现及实体通讯:
拼图的构造方法:
1.赋值 :
public Puzzle(Image Img,int Width, Diff GameDif)// 拼图的图片,宽度(解释:正方形的边长,单位是像素,名字有歧义,抱歉),游戏的难度
游戏的难度决定你分割的程度,分割的程度,决定你存储的数组的大小,如简单对应3行3列,普通对应5行5列,困难对应9行9列
switch(this._gameDif)
{ case Diff.simple: //简单则单元格数组保存为3*3的二维数组
this.N = 3;
node=new Node[3,3]; break; case Diff.ordinary: //一般则为5*5
this.N = 5;
node = new Node[5, 5]; break; case Diff.difficulty: //困难则为9*9
this.N = 9;
node = new Node[9, 9]; break;
}2.分割图片
//分割图片形成各单元保存在数组中
int Count = 0; for (int x = 0; x < this.N; x++)
{ for (int y = 0; y < this.N; y++)
{
node[x, y].Img = CaptureImage(this._img, this.Width / this.N, this.Width / this.N, x * (this.Width / this.N), y * (this.Width / this.N));
node[x, y].Num = Count;
Count++;
}
}其实对单元数组进行赋值的过程,使用双层for循环对二维数组进行遍历操作,然后按序赋值编号node[x,y].Num;
然后对node[x,y].Img,也就是单元的小图片赋值,赋值的方法是,C#的图像的类库,写一个截图方法,使用这个方法,将大图中对应对位置的对应大小的小图截取下来,并保存在node[x,y].Img中;
width/N是什么?是边长除以行数,也就是间隔嘛,间隔也就是每个单元的边长嘛!然后起始坐标(X,Y)起始就是在说,隔了几个单元后,我的位置,
即 :(x,y)=(单元边长*距离起始X轴相距单元数,单元边长*距离起始点Y轴相距单元数);
关于此类问题,希望读者能够多画画图,然后自然就明白了;
public Image CaptureImage(Image fromImage, int width, int height, int spaceX, int spaceY)

主要逻辑:利用DrawImage方法:
//创建新图位图
Bitmap bitmap = new Bitmap(width, height); //创建作图区域
Graphics graphic = Graphics.FromImage(bitmap); //截取原图相应区域写入作图区
graphic.DrawImage(fromImage, 0, 0, new Rectangle(x, y, width, height), GraphicsUnit.Pixel); //从作图区生成新图
Image saveImage = Image.FromHbitmap(bitmap.GetHbitmap());分割了以后,我们要做一个特殊处理,因为我们知道,总有那么一个位置是白的吧?我们默认为最后一个位置,即node[N-1,N-1];
就是写改成了个白色的图片,然后四周的边线都给画成红色,已于被人发现,显著一些,之前的其他单元我也画了边线,但是是白色,也是为了在拼图的观赏性上得到区分。该代码不做介绍。
3.打乱图片:
其实就是将二维数组打乱,我们可以采取一些排序打乱方法,但是请注意!不是每一种打乱都能够复原的!
那么如何做到可行呢?方法理解起来很简单,就是让我们的电脑在开局之前,将完整的有序的单元按照规则中提供的行走方式进行无规则,大次数的行走!也就是说这种方法一定能走回去!
先理解,具体打乱方法,在后面讲解。
移动方法(Move):
拼图游戏中方格的移动,其实就是两个相邻单元的交换,而这两个单元中,必定存在一个白色单元(即上面提到的node[N-1,N-1]单元,他的编号为N*N-1,建议自己动笔算一算)
所以我们的判断条件是,如果移动一个方块,他的上下左右四个方向中,一旦有一个相邻的是白色单元,即N*N-1号单元,则与其交换。这是基本逻辑,但不包括约束条件,当我们的数组达到边界的时候,我们就不能对越界数据进行访问,如当单元为node[0,0]时,你就不能对他上面和右面的数据进行访问,因为Node[-1,0] Node[0,-1]都会越界,发生异常
移动成功,返回TRUE
移动失败,返回FALSE
/// <summary>
/// 移动坐标(x,y)拼图单元 /// </summary>
/// <param name="x">拼图单元x坐标</param>
/// <param name="y">拼图单元y坐标</param>
public bool Move(int x,int y)
{ //MessageBox.Show(" " + node[2, 2].Num);
if (x + 1 != N && node[x + 1, y].Num == N * N - 1)
{
Swap(new Point(x + 1, y), new Point(x, y)); return true;
} if (y + 1 != N && node[x, y + 1].Num == N * N - 1)
{
Swap(new Point(x, y + 1), new Point(x, y)); return true;
}
if (x - 1 != -1 && node[x - 1, y].Num == N * N - 1)
{
Swap(new Point(x - 1, y), new Point(x, y)); return true;
}
if (y - 1 != -1 && node[x, y - 1].Num == N * N - 1)
{
Swap(new Point(x, y - 1), new Point(x, y)); return true;
} return false;
}交换方法(Swap):交换数组中两个元素的位置,该方法不应该被类外访问,顾设置为private私有权限
= = .node[a.X, a.Y] = .node[b.X, b.Y] =
打乱方法:
前面提到,其实就是让电脑帮着乱走一通,说白了就是大量的调用Move(int X,int y)方法,也就是对空白位置的上下左右四个相邻的方块中随机抽取一个,并把它的坐标传递给Move使其进行移动,同样要进行越界考虑,这样的操作大量重复!代码自己看吧 ,利用随机数。
/// <summary>
/// 打乱拼图 /// </summary>
public void Upset()
{ int sum = 100000; if (this._gameDif == Diff.simple) sum = 10000; //if (this._gameDif == Diff.ordinary) sum = 100000;
Random ran = new Random(); for (int i = 0, x = N - 1, y = N - 1; i < sum; i++)
{ long tick = DateTime.Now.Ticks;
ran = new Random((int)(tick & 0xffffffffL) | (int)(tick >> 32)|ran.Next()); switch (ran.Next(0, 4))
{ case 0: if (x + 1 != N)
{
Move(x + 1, y);
x = x + 1;
}
break; case 1: if (y + 1 != N)
{
Move(x, y + 1);
y = y + 1;
}
break; case 2: if (x - 1 != -1)
{
Move(x - 1, y);
x = x - 1;
}
break; case 3: if (y - 1 != -1)
{
Move(x, y - 1);
y = y - 1;
} break;
}
}
}返回图片的方法:
当时怎么起了个这样的鬼名字。。。DisPlay。。。
这个方法与分割方法刚好相背,这个方法其实就是遍历数组,并将其进行组合,组合的方法很简单,就是将他们一个一个的按位置画在一张与原图相等大小的空白图纸上!最后提交图纸,也就是return一个Image;
public Image Display()
{
Bitmap bitmap = new Bitmap(this.Width, this.Width); //创建作图区域
Graphics newGra = Graphics.FromImage(bitmap); for (int x = 0; x < this.N; x++) for (int y = 0; y < this.N; y++)
newGra.DrawImage(node[x, y].Img, new Point(x * this.Width / this.N, y * this.Width / this.N)); return bitmap;
}同样利用的是DrawImage方法,知道如何分割,这个应该很容易理解,自己算一算,在纸上比划比划就明白了;
判断方法:
该方法很容易理解,就是按序按序!遍历所有单元,如果他们的结果中有一个单元的编号
node[x, y].Num 不等于遍历的序号,那么说明,该单元不在原有位置上,即整个图片还没有完成,我们就可以直接返回假值false 如果所有遍历结果都正确,我们可认为,图片已复原,此时返回真值true
count= ( x = ; x < .N; x++ ( y = ; y < .N; y++ (.node[x, y].Num != ++
游戏运行窗口:即游戏玩耍时用于交互的窗口
这里只讲一个方法:即当接受用户鼠标点击事件时我们应该怎么处理并作出什么样反应
其实说白了就这句难懂:
puzzle.Move(e.X / (puzzle.Width / puzzle.N), e.Y / (puzzle.Width / puzzle.N)) 调用了移动方法,移动方块 横坐标为:e.X / (puzzle.Width / puzzle.N)
<em>纵坐标为:e.Y / (puzzle.Width / puzzle.N)<br></em><br><span style="font-size: 15px">我们<a href="http://www.php.cn/wiki/44.html" target="_blank">编程</a>中的<a href="http://www.php.cn/code/12117.html" target="_blank">整数</a>除法和数学里的除法是不一样的!比如10/4数学上等于2余2或者2.5,计算机里直接就是等于2了,只取整数部分<br><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/article/000/000/004/48684ccad126d0d6436ec85a0a36293a-3.jpg" class="lazy" alt=""></span>
行数=行坐标 / 方块边长
列数=列坐标 / 方块边长
我们看P1,P2这两点
P1:40/30*30=1
P2:50/30*30=1
我们会发现同在一个单元格中,无论点击哪个位置,通过这个算法都能转化为
同一个坐标。
(e.x,e.y)为鼠标点击事件点击坐标
private void pictureBox1_MouseClick(object sender, MouseEventArgs e)
{ if (puzzle.Move(e.X / (puzzle.Width / puzzle.N), e.Y / (puzzle.Width / puzzle.N)))
{
Num++;
pictureBox1.Image = puzzle.Display(); if (puzzle.Judge())
{
if (MessageBox.Show("恭喜过关", "是否重新玩一把", MessageBoxButtons.OKCancel) == DialogResult.OK)
{
Num = 0;
puzzle.Upset();
pictureBox1.Image = puzzle.Display();
} else
{
Num = 0;
closefather(); this.Close();
}
}
}
NumLabel.Text = Num.ToString();
}
好,那么大体的逻辑,程序中最需要思考的算法已经讲完了,还有不太懂的地方,欢迎交流~么么哒~


加了点小功能 音乐历史成绩
以上是C#實現《拼圖遊戲》(下)的詳細內容。更多資訊請關注PHP中文網其他相關文章!




