分享一個js數字位數太大導致參數精度遺失的實例
最近遇到個比較奇怪的問題，js函數裡傳參，傳一個位數比較大，印arguments可以看到傳過來的參數已經改變。
然後查了一下，發現確實是js精度遺失造成的。我的解決方法是將數位型改成字元型傳輸，這樣就不會造成精度遺失了。如下圖：
電腦的二進位實作和位數限制有些數無法有限表示。就像有些無理數不能有限表示，如 圓周率 3.1415926...，1.3333... 等。 JS 遵循 IEEE 754 規範，採用雙精度儲存（double precision），佔用 64 bit。如圖
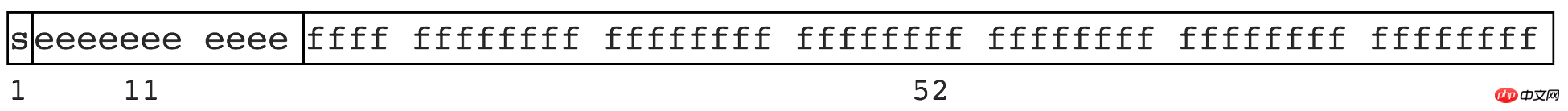
意義
1位元用來表示符號位元
11位元用來表示指數
52位元表示尾數
#浮點數，例如
0.1 >> 0.0001 1001 1001 1001…（1001无限循环） 0.2 >> 0.0011 0011 0011 0011…（0011无限循环）
此時只能模仿十進位進行四捨五入了，但是二進位只有0 和1 兩個，於是變成0 舍1 入。這也就是計算機中部分浮點數運算時出現誤差，丟失精度的根本原因。
大整數的精確度遺失和浮點數本質上是一樣的，尾數位最大是 52 位，因此 JS 中能精確表示的最大整數是 Math.pow(2, 53)，十進位即 9007199254740992。
大於9007199254740992 的可能會遺失精確度
9007199254740992 >> 10000000000000...000 // 共计 53 个 0 9007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 0 9007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0
實際上
9007199254740992 + 1 // 丢失 9007199254740992 + 2 // 未丢失 9007199254740992 + 3 // 丢失 9007199254740992 + 4 // 未丢失
結果如圖
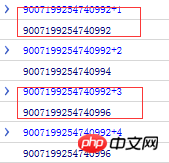
#以上，可以知道看似有窮的數字, 在計算機的二進製表示裡卻是無窮的，由於存儲位數限制因此存在“捨去”，精度丟失就發生了。
想了解更深入的分析可以看这篇论文（又长又臭）：What Every Computer Scientist Should Know About Floating-Point Arithmetic
对于整数，前端出现问题的几率可能比较低，毕竟很少有业务需要需要用到超大整数，只要运算结果不超过 Math.pow(2, 53) 就不会丢失精度。
对于小数，前端出现问题的几率还是很多的，尤其在一些电商网站涉及到金额等数据。解决方式：把小数放到位整数（乘倍数），再缩小回原来倍数（除倍数
// 0.1 + 0.2 (0.1*10 + 0.2*10) / 10 == 0.3 // true
以上是分享一個js數字位數太大導致參數精度遺失的實例的詳細內容。更多資訊請關注PHP中文網其他相關文章！
