交換兩個變數的值且不使用第三個變數的四種法方
int a,b; a=10; b=15;int t; t=a; a=b; b=t;
這個演算法易於理解,特別適合幫助初學者了解電腦程式的特點,是賦值語句的經典應用。在實際軟體開發當中,此演算法簡單明了,不會產生歧義,便於程式設計師之間的交流,一般情況下碰到交換變數值的問題,都應採用此演算法(以下稱為標準演算法)。
上面的演算法最大的缺點就是需要藉助一個臨時變數。那麼不借助臨時變數可以實現交換嗎?答案是肯定的!這裡我們可以用三種演算法來實現:1)算術運算;2)指標位址操作;3)位元運算;4)堆疊實作。
1) 算術運算
int a,b; a=10;b=12; a=b-a; //a=2;b=12b=b-a; //a=2;b=10a=b+a; //a=10;b=10
它的原理是:把a、b看做數軸上的點,圍繞兩點間的距離來進行計算。
此演算法與標準演算法相比,多了三個計算的過程,但是沒有借助臨時變數。 (以下稱為算術演算法)
2) 指標位址操作
因為對位址的運算實際上進行的是整數運算,例如:兩個位址相減得到一個整數,表示兩個變數在記憶體中的儲存位置隔了多少個位元組;位址和一個整數相加即「a+10」表示以a為基底位址的在a後10個a類資料單元的位址。所以理論上可以透過和算術演算法類似的運算來完成位址的交換,從而達到交換變數的目的。即:
int *a,*b; //假设*a=new int(10);*b=new int(20); //&a=0x00001000h,&b=0x00001200ha=(int*)(b-a); //&a=0x00000200h,&b=0x00001200hb=(int*)(b-a); //&a=0x00000200h,&b=0x00001000ha=(int*)(b+int(a)); //&a=0x00001200h,&b=0x00001000h
透過以上運算a、b的位址真的已經完成了交換,且a指向了原先b指向的值,b指向原先a指向的值了嗎?上面的程式碼可以透過編譯,但是執行結果卻令人匪夷所思!原因何在?
有辦法解決嗎?當然!以下是改進的演算法:
if(a<b)
{
a=(int*)(b-a);
b=(int*)(b-(int(a)&0x0000ffff));
a=(int*)(b+(int(a)&0x0000ffff));
}else{
b=(int*)(a-b);
a=(int*)(a-(int(b)&0x0000ffff));
b=(int*)(a+(int(b)&0x0000ffff));
}演算法做的最大改進就是採用位元運算中的與運算“int(a)&0x0000ffff”,因為位址中高16位元為段位址,後16位元為位移位址,將它和0x0000ffff進行與運算後,段位址被屏蔽,只保留位移位址。這樣就原始演算法吻合,從而得到正確的結果。
此演算法同樣沒有使用第三變數就完成了值的交換,與算術演算法比較它顯得不好理解,但是它有它的優點即在交換很大的資料類型時,它的執行速度比算術算法快。因為它交換的時位址,而變數值在記憶體中是沒有移動過的。 (以下稱為地址演算法)3) 位元運算
int a=10,b=12; //a=1010^b=1100;a=a^b; //a=0110^b=1100;b=a^b; //a=0110^b=1010;a=a^b; //a=1100=12;b=1010;
此演算法能夠實現是由異或運算的特點決定的,透過異或運算能夠使資料中的某些位元翻轉,其他位元不變。這意味著任意一個數與任意一個給定的值連續異或兩次,值不變。
int exchange(int x,int y)
{
stack S;
push(S,x);
push(S,y);
x=pop(S);
y=pop(S);
}以上演算法都實作了不借助其他變數來完成兩個變數值的交換,相比較而言算術演算法和位元演算法計算量相當,位址演算法中計算較複雜,卻可以很輕鬆的實作大類型(例如自訂的類別或結構)的交換,而前兩種只能進行整形資料的交換(理論上重載「^」運算符,也可以實現任意結構的交換)。
以上是交換兩個變數的值且不使用第三個變數的四種法方的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 如何使用mdf和mds文件
Feb 19, 2024 pm 05:36 PM
如何使用mdf和mds文件
Feb 19, 2024 pm 05:36 PM
mdf檔案和mds檔案怎麼用隨著電腦科技的不斷進步,我們可以透過多種方式來儲存和共享資料。在數位媒體領域,我們經常會遇到一些特殊的文件格式。在這篇文章中,我們將討論一種常見的文件格式—mdf和mds文件,並介紹它們的使用方法。首先,我們需要了解mdf檔案和mds檔案的含義。 mdf是CD/DVD鏡像檔的副檔名,而mds檔則是mdf檔的元資料檔。
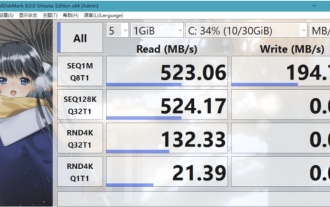 crystaldiskmark是什麼軟體? -crystaldiskmark如何使用?
Mar 18, 2024 pm 02:58 PM
crystaldiskmark是什麼軟體? -crystaldiskmark如何使用?
Mar 18, 2024 pm 02:58 PM
CrystalDiskMark是一款適用於硬碟的小型HDD基準測試工具,可快速測量順序和隨機讀取/寫入速度。接下來就讓小編為大家介紹一下CrystalDiskMark,以及crystaldiskmark如何使用吧~一、CrystalDiskMark介紹CrystalDiskMark是一款廣泛使用的磁碟效能測試工具,用於評估機械硬碟和固態硬碟(SSD)的讀取和寫入速度和隨機I/O性能。它是一款免費的Windows應用程序,並提供用戶友好的介面和各種測試模式來評估硬碟效能的不同方面,並被廣泛用於硬體評
 foobar2000怎麼下載? -foobar2000怎麼使用
Mar 18, 2024 am 10:58 AM
foobar2000怎麼下載? -foobar2000怎麼使用
Mar 18, 2024 am 10:58 AM
foobar2000是一款能隨時收聽音樂資源的軟體,各種音樂無損音質帶給你,增強版本的音樂播放器,讓你得到更全更舒適的音樂體驗,它的設計理念是將電腦端的高級音頻播放器移植到手機上,提供更便捷高效的音樂播放體驗,介面設計簡潔明了易於使用它採用了極簡的設計風格,沒有過多的裝飾和繁瑣的操作能夠快速上手,同時還支持多種皮膚和主題,根據自己的喜好進行個性化設置,打造專屬的音樂播放器支援多種音訊格式的播放,它還支援音訊增益功能根據自己的聽力情況調整音量大小,避免過大的音量對聽力造成損害。接下來就讓小編為大
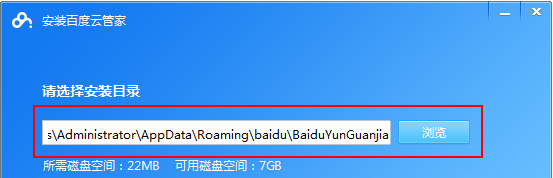 百度網盤app怎麼用
Mar 27, 2024 pm 06:46 PM
百度網盤app怎麼用
Mar 27, 2024 pm 06:46 PM
在如今雲端儲存已成為我們日常生活和工作中不可或缺的一部分。百度網盤作為國內領先的雲端儲存服務之一,憑藉其強大的儲存功能、高效的傳輸速度以及便捷的操作體驗,贏得了廣大用戶的青睞。而且無論你是想要備份重要文件、分享資料,還是在線上觀看影片、聽取音樂,百度網盤都能滿足你的需求。但很多用戶可能對百度網盤app的具體使用方法還不了解,那麼這篇教學就將為大家詳細介紹百度網盤app如何使用,還有疑惑的用戶們就快來跟著本文詳細了解一下吧!百度雲網盤怎麼用:一、安裝首先,下載並安裝百度雲軟體時,請選擇自訂安裝選
 BTCC教學:如何在BTCC交易所綁定使用MetaMask錢包?
Apr 26, 2024 am 09:40 AM
BTCC教學:如何在BTCC交易所綁定使用MetaMask錢包?
Apr 26, 2024 am 09:40 AM
MetaMask(中文也叫小狐狸錢包)是一款免費的、廣受好評的加密錢包軟體。目前,BTCC已支援綁定MetaMask錢包,綁定後可使用MetaMask錢包進行快速登錄,儲值、買幣等,且首次綁定還可獲得20USDT體驗金。在BTCCMetaMask錢包教學中,我們將詳細介紹如何註冊和使用MetaMask,以及如何在BTCC綁定並使用小狐狸錢包。 MetaMask錢包是什麼? MetaMask小狐狸錢包擁有超過3,000萬用戶,是當今最受歡迎的加密貨幣錢包之一。它可免費使用,可作為擴充功能安裝在網絡
 網易信箱大師怎麼用
Mar 27, 2024 pm 05:32 PM
網易信箱大師怎麼用
Mar 27, 2024 pm 05:32 PM
網易郵箱,作為中國網友廣泛使用的一種電子郵箱,一直以來以其穩定、高效的服務贏得了用戶的信賴。而網易信箱大師,則是專為手機使用者打造的信箱軟體,它大大簡化了郵件的收發流程,讓我們的郵件處理變得更加便利。那麼網易信箱大師該如何使用,具體又有哪些功能呢,下文中本站小編將為大家帶來詳細的內容介紹,希望能幫助到大家!首先,您可以在手機應用程式商店搜尋並下載網易信箱大師應用程式。在應用寶或百度手機助手中搜尋“網易郵箱大師”,然後按照提示進行安裝即可。下載安裝完成後,我們打開網易郵箱帳號並進行登錄,登入介面如下圖所示
 教你使用 iOS 17.4「失竊裝置保護」新進階功能
Mar 10, 2024 pm 04:34 PM
教你使用 iOS 17.4「失竊裝置保護」新進階功能
Mar 10, 2024 pm 04:34 PM
Apple在周二推出了iOS17.4更新,為iPhone帶來了一系列新功能和修復。這次更新包含了全新的表情符號,同時歐盟用戶也能夠下載其他應用程式商店。此外,更新還加強了對iPhone安全性的控制,引入了更多的「失竊設備保護」設定選項,為用戶提供更多選擇和保障。 "iOS17.3首次引入了「失竊設備保護」功能,為用戶的敏感資料增加了額外的安全保障。當用戶不在家等熟悉地點時,該功能要求用戶首次輸入生物特徵信息,並在一小時後再次輸入資訊才能存取和更改某些數據,如修改AppleID密碼或關閉失竊設備保護功能
 如何在 Ubuntu 上新增交換空間 22.04 LTS
Feb 20, 2024 am 11:12 AM
如何在 Ubuntu 上新增交換空間 22.04 LTS
Feb 20, 2024 am 11:12 AM
交換空間在Linux系統中扮演著重要角色,特別是在系統記憶體不足時。它充當一個備用的記憶體儲存空間,可以幫助系統平穩運行,即使在負載高的情況下也能保持穩定性。本文為您提供了在Ubuntu22.04LTS上新增交換空間的詳細指南,以確保您的系統效能經過最佳化並能應付各種工作負載。了解交換空間交換空間提供虛擬內存,用於補充系統的實體RAM。當系統的RAM不足時,核心會將資料交換到磁碟,以防止記憶體不足和系統崩潰。 Linux系統常用交換空間來處理這種情況。同時運行多個內存密集型應用程式處理非常大的檔案或數據






