KNN演算法全名為k-Nearest Neighbor,就是K最近鄰的意思。
KNN是一種分類演算法,其基本思想是採用測量不同特徵值之間的距離方法進行分類。
演算法過程如下:
1、準備樣本資料集(樣本中每個資料都已經分好類,並具有分類標籤);
2、使用樣本資料進行訓練;
3、輸入測試資料A;
4、計算A與樣本集的每一個資料之間的距離;
5、依照距離遞增順序排序;
6、選取與A距離最小的k個點;
7、計算前k個點所在類別的出現頻率;
8、返回前k個點出現頻率最高的類別作為A的預測分類。
訓練集太小會誤判,訓練集太大時對測試資料分類的系統開銷會非常大。
什麼是適當的距離測量?距離越近應該意味著這兩個點屬於一個分類的可能性越大。
距離測量包括:
1、歐氏距離
歐幾里德度量(euclidean metric)(也稱為歐氏距離)是一個通常採用的距離定義,指在m維空間中兩點之間的真實距離,或向量的自然長度(即該點到原點的距離)。在二維和三維空間中的歐氏距離就是兩點之間的實際距離。
適用於空間問題。
2、曼哈頓距離
出租車幾何或曼哈頓距離(Manhattan Distance)是由十九世紀的赫爾曼·閔可夫斯基所創詞彙,是種使用在幾何度量空間的幾何學用語,用以標示兩點在標準座標系上的絕對軸距總和。 曼哈頓距離是歐氏距離在歐幾里德空間的固定直角座標系上所形成的線段對軸所產生的投影的距離總和。
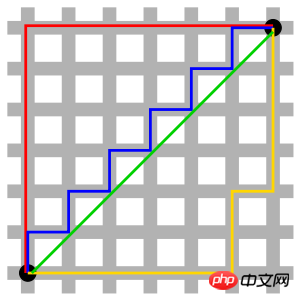
圖中紅線代表曼哈頓距離,綠色代表歐氏距離,也就是直線距離,而藍色和黃色代表等價的曼哈頓距離。 曼哈頓距離-兩點在南北方向上的距離加上在東西向的距離,即d(i,j)=|xi-xj|+|yi-yj|。
適用於路徑問題。
3、切比雪夫距離
在數學中,切比雪夫距離是向量空間中的一種度量,二個點之間的距離定義是其各坐標數值差絕對值的最大值。
切比雪夫距離會用在計算法格中兩點之間的距離,例如:棋盤、倉儲物流等應用。
對一個網格,和一個點的切比雪夫距離為1的點為此點的Moore型鄰居(英語:Moore neighborhood)。

使用於在網格中計算距離的問題。
4、閔可夫斯基距離(Minkowski Distance)
閔氏距離不是一種距離,而是一組距離的定義。
根據變參數的不同,閔氏距離可以表示一類的距離。
其公式中有一個變參p:
當p=1時,是曼哈頓距離;
當p=2時,是歐氏距離;
當p→∞時,就是切比雪夫距離。
5、標準化歐氏距離(Standardized Euclidean distance )
標準化歐氏距離是針對簡單歐氏距離的缺點而作的一種改進方案,可以看成是一種加權歐氏距離。
標準歐氏距離的想法: 既然資料各維度分量的分佈不一樣,那先將各個分量都「標準化」到平均值、變異數相等。
6、馬氏距離(Mahalanobis Distance)
表示資料的協方差距離。
它是一種有效的計算兩個未知樣本集的相似度的方法。
量綱無關,可以排除變數之間的相關性的干擾。
7、巴氏距離(Bhattacharyya Distance) 在統計學中,巴氏距離用於測量兩個離散機率分佈。它常在分類中測量類別之間的可分離性。
8、漢明距離(Hamming distance)
兩個等長字串s1與s2之間的漢明距離定義為將其中一個變成另外一個所需作的最小替換次數。
例如字串「1111」與「1001」之間的漢明距離為2。
應用:
訊息編碼(為了增強容錯性,應使得編碼間的最小漢明距離盡可能大)。
9、夾角餘弦(Cosine)
幾何中夾角餘弦可用於衡量兩個向量方向的差異,資料探勘中可用於衡量樣本向量之間的差異。
10、杰卡德相似係數(Jaccard similarity coefficient)
杰卡德距離以兩個集合中不同元素佔所有元素的比例來衡量兩個集合的區分度。
可將傑卡德相似係數用在測量樣本的相似度上。
11、皮爾森相關係數(Pearson Correlation Coefficient)
皮爾森相關係數,也稱為皮爾森積矩相關係數(Pearson product-moment correlation coefficient) ,是線性相關係數。 皮爾森相關係數是用來反映兩個變數線性相關程度的統計量。
高維度對距離衡量的影響:
當變數數越多,歐式距離的區分能力就越差。
變數值域對距離的影響:
值域越大的變數常常會在距離計算中佔據主導作用,因此應先將變數標準化。
k太小,分類結果易受噪聲點影響,誤差會增大;
k太大,近鄰中又可能包含太多的其它類別的點(對距離加權,可以降低k值設定的影響);
k=N(樣本數),則完全不足取,因為此時無論輸入實例是什麼,都只是簡單的預測它屬於在訓練實例中最多的類,模型過於簡單,忽略了訓練實例中大量有用資訊。
在實際應用中,K值一般會取一個比較小的數值,例如採用交叉驗證法(簡單來說,就是一部分樣本做訓練集,一部分做測試集)來選擇最優的K值。
經驗規則:k一般低於訓練樣本數的平方根。
1、優點
簡單,易於理解,易於實現,精度高,對異常值不敏感。
2、缺點
KNN是一種懶惰演算法,建構模型很簡單,但在對測試資料分類的系統開銷大(計算量大,記憶體開銷大),因為要掃描全部訓練樣本並計算距離。
數值型與標稱型(具有有窮多個不同值,值之間無序)。
例如客戶流失預測、詐欺偵測等。
這裡以python為例描述下基於歐氏距離的KNN演算法實作。
歐氏距離公式:

以歐氏距離為例的範例程式碼:
#! /usr/bin/env python#-*- coding:utf-8 -*-# E-Mail : Mike_Zhang@live.comimport mathclass KNN: def __init__(self,trainData,trainLabel,k):
self.trainData = trainData
self.trainLabel = trainLabel
self.k = k def predict(self,inputPoint):
retLable = "None"arr=[]for vector,lable in zip(self.trainData,self.trainLabel):
s = 0for i,n in enumerate(vector) :
s += (n-inputPoint[i]) ** 2arr.append([math.sqrt(s),lable])
arr = sorted(arr,key=lambda x:x[0])[:self.k]
dtmp = {}for k,v in arr :if not v in dtmp : dtmp[v]=0
dtmp[v] += 1retLable,_ = sorted(dtmp.items(),key=lambda x:x[1],reverse=True)[0] return retLable
data = [
[1.0, 1.1],
[1.0, 1.0],
[0.0, 0.0],
[0.0, 0.1],
[1.3, 1.1],
]
labels = ['A','A','B','B','A']
knn = KNN(data,labels,3)print knn.predict([1.2, 1.1])
print knn.predict([0.2, 0.1])上面的實作比較簡單,在開發中可以使用現成的函式庫,例如scikit-learn :
以上是關於KNN演算法詳細介紹的詳細內容。更多資訊請關注PHP中文網其他相關文章!




