分享Python常用的排序實例
排序演算法的穩定性及意義
冒泡排序
- ##複雜度與穩定性
- 選擇排序
- #插入排序 ##」希爾排序
##快速排序
常見排序演算法效率比較
排序演算法的穩定性與意義
在待排序的序列中,存在具有相同關鍵字的記錄,在排序後這些記錄的相對次序保持不變,則排序演算法是穩定的。 不穩定排序無法完成多個關鍵字的排序。例如整數排序,位數越高的數字優先權越高,從高位數到低位數一次排序。那麼每一位的排序都需要穩定演算法,否則無法得到正確的結果。
即,
當要對多個關鍵字進行多次排序時,必須使用穩定演算法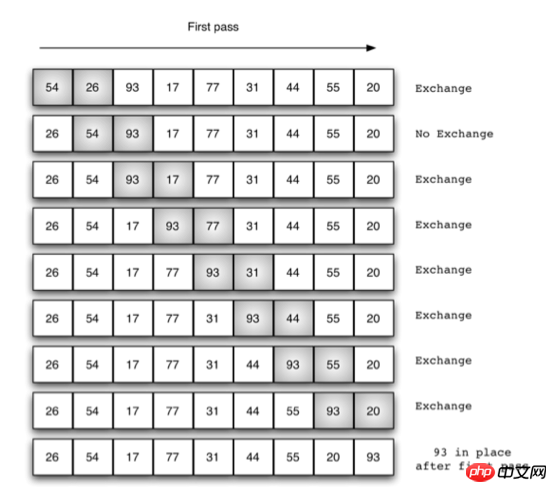
- 
-
def bubble_sort(alist): """ 冒泡排序 """ if len(alist) alist[i+1]: alist[i], alist[i+1] = alist[i+1], alist[i] return alist
登入後複製複雜度與穩定性
最優時間複雜度:\(O(n)\) 遍歷沒有發現任何可以交換的元素,排序結束
最糟時間複雜度:\(O(n^2)\)
#穩定性:穩定

- 選擇排序
選擇排序(Selection sort)是一種簡單直覺的排序演算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然後,再從剩餘未排序元素中繼續尋找最小(大)元素,然後放到已排序序列的末端。以此類推,直到所有元素都排序完畢。
插入排序插入排序透過建立有序序列,對於未排序數據,在已排序序列中從後向前掃描,找到相應位置並插入。插入排序在實作上,從後向前掃描過程中,需要反覆把已排序元素逐步向後挪位,為最新元素提供插入空間。
def insert_sort(alist):
"""
插入排序
"""
n = len(alist)
if n 0:
alist[j], alist[j-1] = alist[j-1], alist[j]
j-=1
return alist
登入後複製
複雜度與穩定性def insert_sort(alist): """ 插入排序 """ n = len(alist) if n 0: alist[j], alist[j-1] = alist[j-1], alist[j] j-=1 return alist
#最優時間複雜度:O(\(n\)) (升序排列,序列已經處於升序狀態)
- 最壞時間複雜度:O(\(n^2\))
- 穩定性:穩定
- 希爾排序希爾排序(Shell Sort)是插入排序的改進, 排序非穩定。希爾排序是把記錄按標的一定 增量
def shell_sort(alist):
n = len(alist)
gap = n//2
# gap 变化到0之前,插入算法之行的次数
while gap > 0:
# 希尔排序, 与普通的插入算法的区别就是gap步长
for i in range(gap,n):
j = i
while alist[j] 0:
alist[j], alist[j-gap] = alist[j-gap], alist[j]
j-=gap
gap = gap//2
return alist
登入後複製
複雜度與穩定性
最優時間複雜度:\(O(n^{1.3})\) (不要求本身有順序)def shell_sort(alist): n = len(alist) gap = n//2 # gap 变化到0之前,插入算法之行的次数 while gap > 0: # 希尔排序, 与普通的插入算法的区别就是gap步长 for i in range(gap,n): j = i while alist[j] 0: alist[j], alist[j-gap] = alist[j-gap], alist[j] j-=gap gap = gap//2 return alist
- 最壞時間複雜度:\(O(n^2)\)
- 穩定性:不穩定
- 快速排序
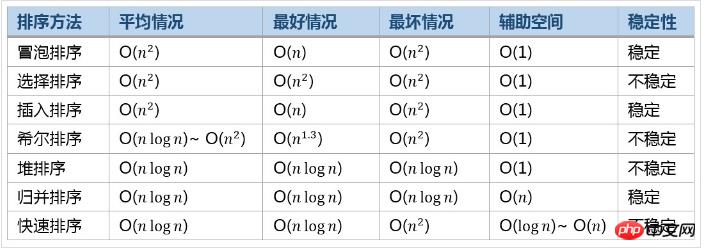 #########重新排序數列,所有元素比基準值小的擺放在基準前面,所有元素比基準值大的擺在基準的後面(相同的數可以到任一邊)。在這個分區結束之後,該基準就處於數列的中間位置。這個稱為分區(partition)操作。 ############遞歸地(recursive)把小於基準值元素的子數列和大於基準值元素的子數列排序。 ############遞歸的最底部情形,是數列的大小是零或一,也就是永遠都已經被排序好了。雖然一直遞歸下去,但是這個演算法總是會結束,因為在每次的迭代(iteration)中,它至少會把一個元素擺到它最後的位置去。 ######常見排序演算法效率比較############
#########重新排序數列,所有元素比基準值小的擺放在基準前面,所有元素比基準值大的擺在基準的後面(相同的數可以到任一邊)。在這個分區結束之後,該基準就處於數列的中間位置。這個稱為分區(partition)操作。 ############遞歸地(recursive)把小於基準值元素的子數列和大於基準值元素的子數列排序。 ############遞歸的最底部情形,是數列的大小是零或一,也就是永遠都已經被排序好了。雖然一直遞歸下去,但是這個演算法總是會結束,因為在每次的迭代(iteration)中,它至少會把一個元素擺到它最後的位置去。 ######常見排序演算法效率比較############
以上是分享Python常用的排序實例的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

熱門話題
 PHP和Python:代碼示例和比較
Apr 15, 2025 am 12:07 AM
PHP和Python:代碼示例和比較
Apr 15, 2025 am 12:07 AM
PHP和Python各有優劣,選擇取決於項目需求和個人偏好。 1.PHP適合快速開發和維護大型Web應用。 2.Python在數據科學和機器學習領域佔據主導地位。
 CentOS上如何進行PyTorch模型訓練
Apr 14, 2025 pm 03:03 PM
CentOS上如何進行PyTorch模型訓練
Apr 14, 2025 pm 03:03 PM
在CentOS系統上高效訓練PyTorch模型,需要分步驟進行,本文將提供詳細指南。一、環境準備:Python及依賴項安裝:CentOS系統通常預裝Python,但版本可能較舊。建議使用yum或dnf安裝Python3併升級pip:sudoyumupdatepython3(或sudodnfupdatepython3),pip3install--upgradepip。 CUDA與cuDNN(GPU加速):如果使用NVIDIAGPU,需安裝CUDATool
 CentOS上PyTorch的GPU支持情況如何
Apr 14, 2025 pm 06:48 PM
CentOS上PyTorch的GPU支持情況如何
Apr 14, 2025 pm 06:48 PM
在CentOS系統上啟用PyTorchGPU加速,需要安裝CUDA、cuDNN以及PyTorch的GPU版本。以下步驟將引導您完成這一過程:CUDA和cuDNN安裝確定CUDA版本兼容性:使用nvidia-smi命令查看您的NVIDIA顯卡支持的CUDA版本。例如,您的MX450顯卡可能支持CUDA11.1或更高版本。下載並安裝CUDAToolkit:訪問NVIDIACUDAToolkit官網,根據您顯卡支持的最高CUDA版本下載並安裝相應的版本。安裝cuDNN庫:前
 docker原理詳解
Apr 14, 2025 pm 11:57 PM
docker原理詳解
Apr 14, 2025 pm 11:57 PM
Docker利用Linux內核特性,提供高效、隔離的應用運行環境。其工作原理如下:1. 鏡像作為只讀模板,包含運行應用所需的一切;2. 聯合文件系統(UnionFS)層疊多個文件系統,只存儲差異部分,節省空間並加快速度;3. 守護進程管理鏡像和容器,客戶端用於交互;4. Namespaces和cgroups實現容器隔離和資源限制;5. 多種網絡模式支持容器互聯。理解這些核心概念,才能更好地利用Docker。
 Python vs. JavaScript:社區,圖書館和資源
Apr 15, 2025 am 12:16 AM
Python vs. JavaScript:社區,圖書館和資源
Apr 15, 2025 am 12:16 AM
Python和JavaScript在社區、庫和資源方面的對比各有優劣。 1)Python社區友好,適合初學者,但前端開發資源不如JavaScript豐富。 2)Python在數據科學和機器學習庫方面強大,JavaScript則在前端開發庫和框架上更勝一籌。 3)兩者的學習資源都豐富,但Python適合從官方文檔開始,JavaScript則以MDNWebDocs為佳。選擇應基於項目需求和個人興趣。
 CentOS下PyTorch版本怎麼選
Apr 14, 2025 pm 02:51 PM
CentOS下PyTorch版本怎麼選
Apr 14, 2025 pm 02:51 PM
在CentOS下選擇PyTorch版本時,需要考慮以下幾個關鍵因素:1.CUDA版本兼容性GPU支持:如果你有NVIDIAGPU並且希望利用GPU加速,需要選擇支持相應CUDA版本的PyTorch。可以通過運行nvidia-smi命令查看你的顯卡支持的CUDA版本。 CPU版本:如果沒有GPU或不想使用GPU,可以選擇CPU版本的PyTorch。 2.Python版本PyTorch
 minio安裝centos兼容性
Apr 14, 2025 pm 05:45 PM
minio安裝centos兼容性
Apr 14, 2025 pm 05:45 PM
MinIO對象存儲:CentOS系統下的高性能部署MinIO是一款基於Go語言開發的高性能、分佈式對象存儲系統,與AmazonS3兼容。它支持多種客戶端語言,包括Java、Python、JavaScript和Go。本文將簡要介紹MinIO在CentOS系統上的安裝和兼容性。 CentOS版本兼容性MinIO已在多個CentOS版本上得到驗證,包括但不限於:CentOS7.9:提供完整的安裝指南,涵蓋集群配置、環境準備、配置文件設置、磁盤分區以及MinI
 CentOS上PyTorch的分佈式訓練如何操作
Apr 14, 2025 pm 06:36 PM
CentOS上PyTorch的分佈式訓練如何操作
Apr 14, 2025 pm 06:36 PM
在CentOS系統上進行PyTorch分佈式訓練,需要按照以下步驟操作:PyTorch安裝:前提是CentOS系統已安裝Python和pip。根據您的CUDA版本,從PyTorch官網獲取合適的安裝命令。對於僅需CPU的訓練,可以使用以下命令:pipinstalltorchtorchvisiontorchaudio如需GPU支持,請確保已安裝對應版本的CUDA和cuDNN,並使用相應的PyTorch版本進行安裝。分佈式環境配置:分佈式訓練通常需要多台機器或單機多GPU。所






