註：因為「子集與問題」的學習不夠深入，所以本文在講解動態規劃遞推公式中可能存在敘述不清，或者錯誤的地方，如有發現望能不吝賜教。
子集與問題可描述如下：給定n個正整數W=(w #1, w2, …, wn)與正整數M，要求尋找這樣一個子集I⊆{1, 2, 3, ..., n},使得∑wi=M,i∈I[1] 。舉個例子對子集和問題做一個通俗的解釋：集合W=(1, 2, 3, 4, 5)，給定一個正整數#M =5，是否存在W#的子集#，使得子集 #I中的元素相加等於M，這個例子顯然存在子集I=(2, 3)。
問題定義：正整數集合S=(w1, w2, w3, …，wn)，給定正整數W，s[i, j]中的##i表示S的子集，j表示子集i的和。如果S的某個集合i元素之和j=M##，即問題有解。 舉例：
S=(7, 34, 4, 12, 5, 3)，W=6 #，是否存在S的子集，它的元素總和等於W。 這個問題同樣有多種解法，在本文中利用動態規劃的想法來求解，那麼就需要推導出一個遞推公式。我們將集合
S不斷的分割成小的集合，這就是動態規劃的第一步：定義子問題。集合S最小的集合就是空集合，空集合當然不存在它的元素總和等於W，當然若j=0的情況下空集合是符合條件的。
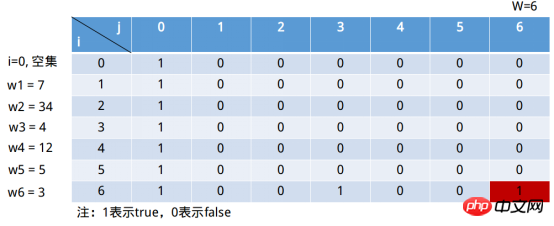
這個表格的欄位代表的是集合中的元素總和，最多只到達元素W，大於##W當然沒意義了。只要在j=6列中出現1，即得到問題的解。行表示前i個（包括i）元素組成的子集（這句話可能會有點疑問，這樣豈不是掃描不到所有情況嗎？ i=0表示為空集合。 j=6時，空集合情況為true#。那麼當j=0時，這樣對任意子集和都成立（空集合是它們的子集）。所以表格繼續填入如下圖。 動態規劃的第三步：定義初始狀態。狀態規劃第二步則是定義狀態轉移規則，即狀態之間的遞推關係。 中的i表示的是前i
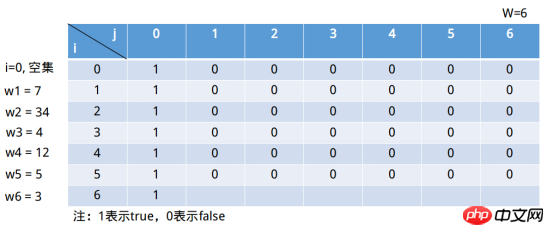
難於理解的是第2)種情況。對於第二種情況能明確一點就是s[i, X]中的i是確定的，關鍵是j，j此時如何定義？利用數學中的「特值法」#，舉例集合(3, 34, 9)，是否存在給定子集的元素總和等於37##i=2（子集為(3, 34)），j = 37，此時「 #包括第i個元素的前i子集」這種情況下，s[2, 37] => s[2, 37 - 34] = s[2, 3]，子集(3 , 34)當然存在它的子集元素總和等於3。那如果j = 36，s[2, 36] => s[2, 36 - 34] = s[2, 2]，子集(3, 34)顯然不存在它的子集元素總和等於2。那j = 1呢， #，此時 s[2, 1] => s[2 - 1, 1] = s[1, 1]，子集(3)顯然不存在它的子集元素總和等於1。 綜上，遞推式如下圖： 在用程式碼實作這個演算法前，先透過遞推公式填入上面的矩陣。 ①i = 1, 此時子集為(7)， ②i = 1，此时子集为(7)，j = 2，j ∉ (∅)，选择情况2) => s[0, 2] || s[1, -5]（i = 0表示空集）。显然s[1, 2] = 0。 …… ⑥i = 1，此时子集为(7)，j = 6，j ∉ (∅)，选择情况2) => s[0, 6] || s[1, -1]（i = 0表示空集）。显然s[1, 6] = 0。 最后填充为如下图所示： 继续填充最后一行： ①i = 6, 此时子集为(7, 34, 4, 12, 5, 3)，j = 1，j ∉ (7, 34, 4, 12, 5)，选择情况2) => s[5, 1] || s[6, -2]（i = 0表示空集）。显然s[6, 1] = 0。 ②i = 6, 此时子集为(7, 34, 4, 12, 5, 3)，j = 2，j ∉ (7, 34, 4, 12, 5)，选择情况2) => s[5, 1] || s[6, -1]（i = 0表示空集）。显然s[6, 2] = 0。 ③i = 6, 此时子集为(7, 34, 4, 12, 5, 3)，j = 3，j ∉ (7, 34, 4, 12, 5)，选择情况2) => s[5, 1] || s[6, 0]。显然s[6, 3] = 1。 ... ⑥i = 6, 此时子集为(7, 34, 4, 12, 5, 3), j = 6, j ∉ (7, 34, 4, 12, 5)，选择情况2) => s[5, 6] || s[6, 3]。显然s[6, 6] = 1。 Java Python3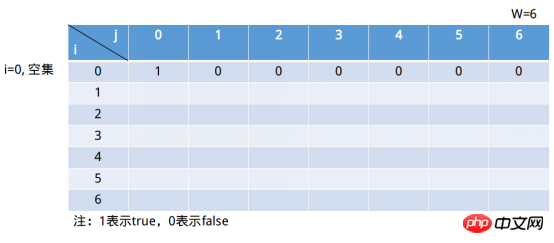
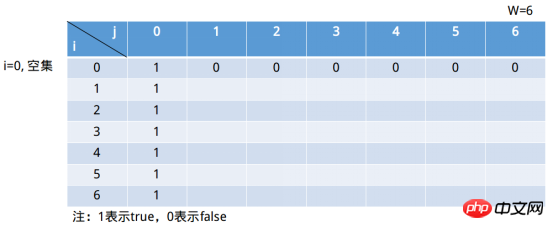
個子集(包括i)。實際上我們從這裡進行劃分為兩部分： 1)不包括第i個元素的前#i個子集，即
j - wi < 0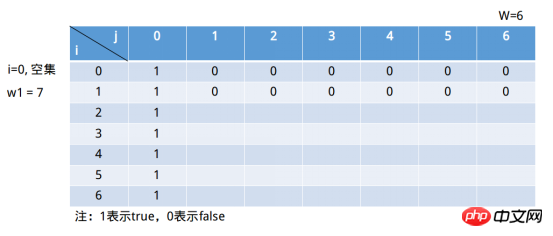
1 package com.algorithm.dynamicprogramming; 2 3 import java.util.Arrays; 4 5 /** 6 * 子集和问题 7 * Created by yulinfeng on 7/2/17. 8 */ 9 public class SubsetSumProblem {10 11 public static void main(String[] srgs) {12 int[] sets = {7, 34, 4, 12, 5, 3};13 int sum = 87;14 boolean isExistSubSet = subsetSumProblem(sets, sum);15 System.out.println("集合" + Arrays.toString(sets) + "是否存在子集的和等于" + sum + ":" + isExistSubSet);16 }17 18 private static boolean subsetSumProblem(int[] sets, int sum) {19 int row = sets.length + 1;20 int col = sum + 1;21 int[][] solutionMatrix = new int[row][col];22 solutionMatrix[0][0] = 1;23 24 /**25 * 0 1 2 3 4 5 626 * 0 |1|0|0|0|0|0|0|27 * 1 |x|x|x|x|x|x|x|28 * 2 |x|x|x|x|x|x|x|29 * 3 |x|x|x|x|x|x|x|30 * 3 |x|x|x|x|x|x|x|31 * 4 |x|x|x|x|x|x|x|32 * 5 |x|x|x|x|x|x|x|33 * 6 |x|x|x|x|x|x|x|34 */35 for (int i = 1; i < col; i++) {36 solutionMatrix[0][i] = 0;37 }38 /**39 * 初始状态40 * 0 1 2 3 4 5 641 * 0 |1|0|0|0|0|0|0|42 * 1 |1|0|x|x|x|x|x|43 * 2 |x|x|x|x|x|x|x|44 * 3 |x|x|x|x|x|x|x|45 * 3 |x|x|x|x|x|x|x|46 * 4 |x|x|x|x|x|x|x|47 * 5 |x|x|x|x|x|x|x|48 * 6 |1|0|0|x|x|x|x|49 * [i][0] = 1，按行填充50 */51 for (int i = 1; i < row; i++) {52 solutionMatrix[i][0] = 1;53 for (int j = 1; j < col; j++) {54 solutionMatrix[i][j] = solutionMatrix[i - 1][j];55 56 if (solutionMatrix[i][j] == 1) {57 solutionMatrix[i][j] = solutionMatrix[i][j];58 } else if ( j - sets[i - 1] >= 0 && solutionMatrix[i][j - sets[i - 1]] == 1) {59 solutionMatrix[i][j] = solutionMatrix[i][j - sets[i - 1]];60 } else {61 solutionMatrix[i][j] = 0;62 }63 64 if (j == col - 1 && solutionMatrix[i][j] == 1) {65 return true;66 }67 }68 }69 70 return false;71 }72 } 1 def subset_sum_problem(sets, sum): 2 row = len(sets) + 1 3 col = sum + 1 4 solutionMatrix = [[0 for col in range(col)] for row in range(row)] 5 solutionMatrix[0][0] = 1 6 for i in range(1, col): 7 solutionMatrix[0][i] = 0 8 9 for j in range(1, row):10 solutionMatrix[j][0] = 111 for k in range(1, col):12 solutionMatrix[j][k] = solutionMatrix[j - 1][k]13 if solutionMatrix[j][k] == 1:14 solutionMatrix[j][k] = solutionMatrix[j][k]15 elif (k - sets[j - 1] >= 0) and (solutionMatrix[j][k - sets[j - 1]] == 1):16 solutionMatrix[j][k] = solutionMatrix[j][k - sets[j - 1]]17 else:18 solutionMatrix[j][k] = 019 if k == col - 1 and solutionMatrix[j][k] == 1:20 return True21 22 return False23 24 sets = [7, 34, 4, 12, 5, 3]25 num = 626 is_exist = subset_sum_problem(sets, num)27 print(is_exist)
以上是子集和問題的實例詳解的詳細內容。更多資訊請關注PHP中文網其他相關文章！
