這篇文章主要學習Python常用演算法，Python常用排序演算法，具有一定的參考價值，有興趣的小夥伴可以參考一下
本節內容
演算法定義
時間複雜度
空間複雜度
常用演算法實例
#1.演算法定義
#演算法（Algorithm）是指解題方案的準確而完整的描述，是一系列解決問題的清晰指令，演算法代表著用系統的方法描述解決問題的策略機制。也就是說，能夠對某一規範的輸入，在有限時間內獲得所要求的輸出。如果一個演算法有缺陷，或不適合某個問題，執行這個演算法就不會解決這個問題。不同的演算法可能用不同的時間、空間或效率來完成同樣的任務。一個演算法的優劣可以用空間複雜度與時間複雜度來衡量。
一個演算法應該具有以下七個重要的特徵：
①有窮性（Finiteness）：演算法的有窮性是指演算法必須能在執行有限個步驟之後終止；
②確切性(Definiteness)：演算法的每一步驟必須有確切的定義；
③輸入項目(Input)：一個演算法有0個或多個輸入，以刻畫運算對象的初始情況，所謂0個輸 入是指演算法本身定出了初始條件；
④輸出項(Output)：一個演算法有一個或多個輸出，以反映輸入資料加工後的結果。沒 有輸出的演算法是毫無意義的；
⑤可行性(Effectiveness)：演算法中執行的任何計算步驟都是可以分解為基本的可執行 的操作步，即每個計算步都可以在有限時間內完成（也稱之為有效性）；
⑥高效性(High efficiency)：執行速度快，佔用資源少；
⑦健壯性(Robustness) ：對數據響應正確。
2. 時間複雜度
電腦科學中，演算法的時間複雜度是一個函數，它定量描述了該演算法的運行時間,時間複雜度常用大O符號（大O符號（Big O notation）是用來描述函數漸進式的數學符號。更確切地說，它是用另一個（通常較簡單的）函數來描述一個函數數量級的漸近上界。 ，使用這種方式時，時間複雜度可稱為是漸近的，它考察當輸入值大小趨近無窮時的情況。
大O，簡而言之可以認為它的意思是「order of」（大約是）。
無窮大漸近
大O符號在分析演算法效率的時候非常有用。舉個例子，解決一個規模為 n 的問題所花費的時間（或所需步驟的數目）可以被求得：T(n) = 4n^2 - 2n + 2。
當n 增加時，n^2; 項將開始占主導地位，而其他各項可以被忽略－舉例說明：當n = 500，4n^2; 項是2n 項的1000倍大，因此在大多數場合下，省略後者對表達式的值的影響將是可以忽略的。
數學表示掃盲貼python演算法表示概念掃盲教學
一、計算方法
1.演算法執行所耗費的時間，從理論上是不能算出來的，必須上機運行測試才能知道。但我們不可能也沒有必要對每個演算法都上機測試，只要知道哪個演算法花費的時間多，哪個演算法花費的時間少就可以了。而一個演算法花費的時間與演算法中語句的執行次數成正比例，哪個演算法中語句執行次數多，它花費時間就多。
一個演算法中的語句執行次數稱為語句頻度或時間頻度。記為T(n)。
2.一般情況下，演算法的基本運算重複執行的次數是模組n的某一個函數f（n），因此，演算法的時間複雜度記做：T（ n）=O（f（n））。隨著模組n的增大，演算法執行的時間的成長率和f（n）的成長率成正比，所以f（n）越小，演算法的時間複雜度越低，演算法的效率越高。
在計算時間複雜度的時候，先找出演算法的基本操作，然後根據對應的各語句確定它的執行次數，再找出T（n）的同數量級（它的同數量級有以下：1 ，Log2n ，n ，nLog2n ，n的平方，n的三次方，2的n次方，n！可得到一常數c，則時間複雜度T（n）=O（f（n））。
3.常見的時間複雜度
以數量級遞增排列，常見的時間複雜度有：
常數階O(1), 對數階O(log2n), 線性階O(n), 線性對數階O(nlog2n), 平方階O(n^2)， 立方階O(n^3),...， k次方階O(n ^k), 指數階O(2^n) 。
其中，
1.O(n)，O(n^2)， 立方階O(n^3),...， k次方階O(n^k) 為多項式階時間複雜度，分別稱為一階時間複雜度，二階時間複雜度。 。 。 。
2.O(2^n)，指數階時間複雜度，該種不實用
3.對數階O(log2n), 線性對數階O(nlog2n)，除了常數階以外，該種效率最高
範例：演算法：
for（i=1;i<=n;++i）
{
for(j=1;j<=n;++j)
{
c[ i ][ j ]=0; //该步骤属于基本操作 执行次数：n^2
for(k=1;k<=n;++k)
c[ i ][ j ]+=a[ i ][ k ]*b[ k ][ j ]; //该步骤属于基本操作 执行次数：n^3
}
}登入後複製
則有T（n）= n^2+n^3，根據上面括號裡的同數量級，我們可以確定n^3為T（n）的同數量級
則有f（n）= n^3，然後根據T（n）/f（n）求極限可得到常數c
則該演算法的時間複雜度：T（n）=O（n^3)
四、 定義：如果一個問題的規模是n ，解這一問題的某一演算法所需的時間為T(n)，它是n的某一函數T(n)稱為此演算法的「時間複雜度」。
當輸入量n逐漸加大時，時間複雜度的極限情形稱為演算法的「漸近時間複雜度」。
我們常用大O表示法表示時間複雜性，注意它是某一個演算法的時間複雜性。大O表示只是說有上界，由定義如果f(n)=O(n)，那顯然成立f(n)=O(n^2)，它給你一個上界，但並不是上確界，但人們在表示的時候一般都習慣表示前者。
此外，一個問題本身也有它的複雜性，如果某個演算法的複雜性到達了這個問題複雜性的下界，那就稱這樣的演算法是最佳演算法。
「大O記法」：在這個描述中使用的基本參數是 n，也就是問題實例的規模，把複雜性或運行時間表達為n的函數。這裡的「O」表示量級(order)，比如說「二分檢索是O(logn)的」,也就是說它需要「透過logn量級的步驟去檢索一個規模為n的數組」記法O ( f(n) )表示當n增大時，運轉時間至多將以正比於f(n)的速度增長。
這種漸進估計對演算法的理論分析和大致比較是非常有價值的，但在實務上細節也可能造成差異。例如，一個低附加代價的O(n2)演算法在n較小的情況下可能比一個高附加代價的 O(nlogn)演算法運行得更快。當然，隨著n夠大以後，具有較慢上升函數的演算法必然會運作得更快。
的頻度均為1，該程序段的執行時間為與問題規模n無關的常數。演算法的時間複雜度為常數階，記作T(n)=O(1)。如果演算法的執行時間不隨著問題規模n的增加而成長，即使演算法中有上千條語句，其執行時間也不過是一個較大的常數。此類演算法的時間複雜度是O(1)。
O(n^2)
2.1. 交換i與j的內容
sum=0； （一次) for(i=1;i sum++； （n^2次）
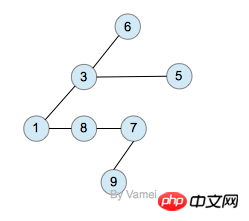
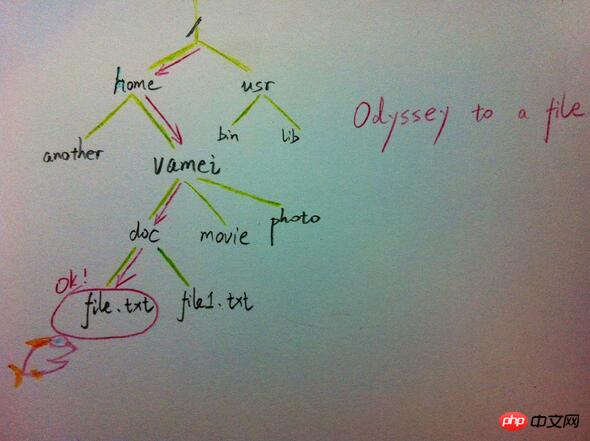
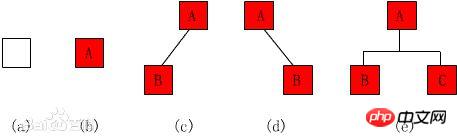
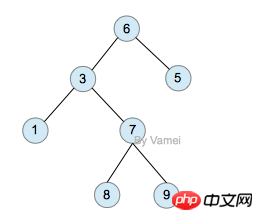
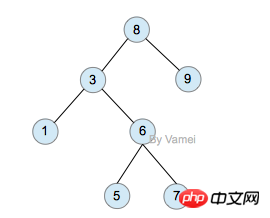
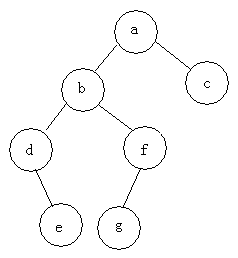
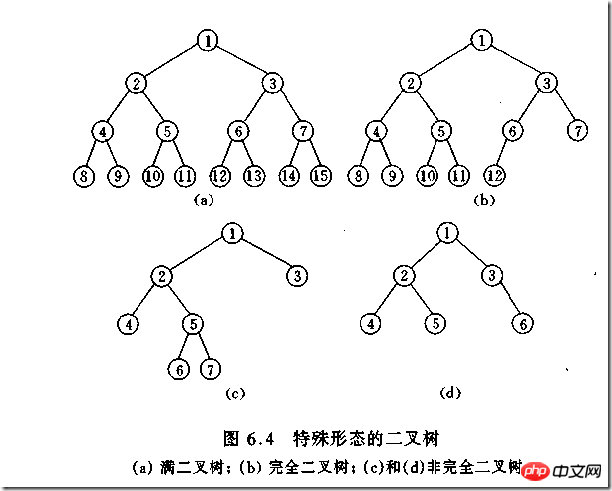
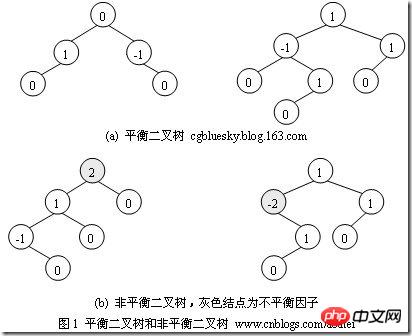
解：T(n)=2n^2+n+1 =O(n^2) # for (i=1;i { y=y+1; 與++;
x++; 度是(n-1)*(2n+1)=2n^2-n -1
f(n)=2n^2-n-1+(n-1)=2n^2-2
此程序的時間複雜度T(n)=O(n^2).
O(n)
#2.3.
#
a=0;
b=1; ①
for (i=1;i<=n;i++) ②
{
s=a+b; ③
b=a; ④
a=s; ⑤
}
解：语句1的频度：2,
语句2的频度： n,
语句3的频度： n-1,
语句4的频度：n-1,
语句5的频度：n-1,
T(n)=2+n+3(n-1)=4n-1=O(n).
O(log2n )
2.4.
i=1; ①
while (i<=n)
i=i*2; ②
解： 语句1的频度是1,
设语句2的频度是f(n), 则：2^f(n)<=n;f(n)<=log2n
取最大值f(n)= log2n,
T(n)=O(log2n )
O(n^3)
2.5.
for(i=0;i {
for(j=0;j {
for(k=0;k x=x+2;
}
}
解：当i=m, j=k的时候,内层循环的次数为k当i=m时, j 可以取 0,1,...,m-1 , 所以这里最内循环共进行了0+1+...+m-1=(m-1)m/2次所以,i从0取到n, 则循环共进行了: 0+(1-1)*1/2+...+(n-1)n/2=n(n+1)(n-1)/6所以时间复杂度为O(n^3).
我们还应该区分算法的最坏情况的行为和期望行为。如快速排序的最 坏情况运行时间是 O(n^2)，但期望时间是 O(nlogn)。通过每次都仔细 地选择基准值，我们有可能把平方情况 (即O(n^2)情况)的概率减小到几乎等于 0。在实际中，精心实现的快速排序一般都能以 (O(nlogn)时间运行。
下面是一些常用的记法：
访问数组中的元素是常数时间操作，或说O(1)操作。一个算法如 果能在每个步骤去掉一半数据元素，如二分检索，通常它就取 O(logn)时间。用strcmp比较两个具有n个字符的串需要O(n)时间。常规的矩阵乘算法是O(n^3)，因为算出每个元素都需要将n对 元素相乘并加到一起，所有元素的个数是n^2。
指数时间算法通常来源于需要求出所有可能结果。例如，n个元 素的集合共有2n个子集,所以要求出所有子集的算法将是O(2n)的。指数算法一般说来是太复杂了，除非n的值非常小，因为，在 这个问题中增加一个元素就导致运行时间加倍。不幸的是，确实有许多问题 (如著名的“巡回售货员问题” )，到目前为止找到的算法都是指数的。如果我们真的遇到这种情况，通常应该用寻找近似最佳结果的算法替代之。
常用排序
冒泡排序（Bubble Sort）
冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。
它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。
这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端，故名。
data_set = [ 9,1,22,31,45,3,6,2,11 ]
loop_count = 0
for j in range(len(data_set)):
for i in range(len(data_set) - j- 1): # -1 是因为每次比对的都 是i 与i +1,不减1的话,最后一次对比会超出list 获取范围,-j是因为,每一次大loop就代表排序好了一个最大值,放在了列表最后面,下次loop就不用再运算已经排序好了的值 了
if data_set[i] > data_set[i+1]: #switch
tmp = data_set[i]
data_set[i] = data_set[i+1]
data_set[i+1] = tmp
loop_count +=1
print(data_set)
print(data_set)
print("loop times", loop_count)登入後複製
选择排序
The algorithm works by selecting the smallest unsorted item and then swapping it with the item in the next position to be filled.
The selection sort works as follows: you look through the entire array for the smallest element, once you find it you swap it (the smallest element) with the first element of the array. Then you look for the smallest element in the remaining array (an array without the first element) and swap it with the second element. Then you look for the smallest element in the remaining array (an array without first and second elements) and swap it with the third element, and so on. Here is an example,
data_set = [ 9,1,22,31,45,3,6,2,11 ]
smallest_num_index = 0 #初始列表最小值,默认为第一个
loop_count = 0
for j in range(len(data_set)):
for i in range(j,len(data_set)):
if data_set[i] < data_set[smallest_num_index]: #当前值 比之前选出来的最小值 还要小,那就把它换成最小值
smallest_num_index = i
loop_count +=1
else:
print("smallest num is ",data_set[smallest_num_index])
tmp = data_set[smallest_num_index]
data_set[smallest_num_index] = data_set[j]
data_set[j] = tmp
print(data_set)
print("loop times", loop_count)登入後複製
The worst-case runtime complexity is O(n2).
插入排序(Insertion Sort)
插入排序(Insertion Sort)的基本思想是：将列表分为2部分，左边为排序好的部分，右边为未排序的部分，循环整个列表，每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子序列中的适当位置，直到全部记录插入完成为止。
插入排序非常类似于整扑克牌。
在开始摸牌时，左手是空的，牌面朝下放在桌上。接着，一次从桌上摸起一张牌，并将它插入到左手一把牌中的正确位置上。为了找到这张牌的正确位置，要将它与手中已有的牌从右到左地进行比较。无论什么时候，左手中的牌都是排好序的。
也许你没有意识到，但其实你的思考过程是这样的：现在抓到一张7，把它和手里的牌从右到左依次比较，7比10小，应该再往左插，7比5大，好，就插这里。为什么比较了10和5就可以确定7的位置？为什么不用再比较左边的4和2呢？因为这里有一个重要的前提：手里的牌已经是排好序的。现在我插了7之后，手里的牌仍然是排好序的，下次再抓到的牌还可以用这个方法插入。编程对一个数组进行插入排序也是同样道理，但和插入扑克牌有一点不同，不可能在两个相邻的存储单元之间再插入一个单元，因此要将插入点之后的数据依次往后移动一个单元。
source = [92, 77, 67, 8, 6, 84, 55, 85, 43, 67]
for index in range(1,len(source)):
current_val = source[index] #先记下来每次大循环走到的第几个元素的值
position = index
while position > 0 and source[position-1] > current_val: #当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
source[position] = source[position-1] #把左边的一个元素往右移一位
position -= 1 #只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止
source[position] = current_val #已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
print(source)
登入後複製
结果：
[77, 92, 67, 8, 6, 84, 55, 85, 43, 67]
[67, 77, 92, 8, 6, 84, 55, 85, 43, 67]
[8, 67, 77, 92, 6, 84, 55, 85, 43, 67]
[6, 8, 67, 77, 92, 84, 55, 85, 43, 67]
[6, 8, 67, 77, 84, 92, 55, 85, 43, 67]
[6, 8, 55, 67, 77, 84, 92, 85, 43, 67]
[6, 8, 55, 67, 77, 84, 85, 92, 43, 67]
[6, 8, 43, 55, 67, 77, 84, 85, 92, 67]
[6, 8, 43, 55, 67, 67, 77, 84, 85, 92]
#更容易理解的版本
data_set = [ 9,1,22,9,31,-5,45,3,6,2,11 ]
for i in range(len(data_set)):
#position = i
while i > 0 and data_set[i] < data_set[i-1]:# 右边小于左边相邻的值
tmp = data_set[i]
data_set[i] = data_set[i-1]
data_set[i-1] = tmp
i -= 1
# position = i
# while position > 0 and data_set[position] < data_set[position-1]:# 右边小于左边相邻的值
# tmp = data_set[position]
# data_set[position] = data_set[position-1]
# data_set[position-1] = tmp
# position -= 1
登入後複製
快速排序（quick sort）
设要排序的数组是A[0]……A[N-1]，首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为一趟快速排序。值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动
注：在待排序的文件中，若存在多个关键字相同的记录，经过排序后这些具有相同关键字的记录之间的相对次序保持不变，该排序方法是稳定的；若具有相同关键字的记录之间的相对次序发生改变，则称这种排序方法是不稳定的。
要注意的是，排序算法的稳定性是针对所有输入实例而言的。即在所有可能的输入实例中，只要有一个实例使得算法不满足稳定性要求，则该排序算法就是不稳定的。
排序演示
示例
假设用户输入了如下数组：
创建变量i=0（指向第一个数据）, j=5(指向最后一个数据), k=6(赋值为第一个数据的值)。
我们要把所有比k小的数移动到k的左面，所以我们可以开始寻找比6小的数，从j开始，从右往左找，不断递减变量j的值，我们找到第一个下标3的数据比6小，于是把数据3移到下标0的位置，把下标0的数据6移到下标3，完成第一次比较：
i=0 j=3 k=6
接着，开始第二次比较，这次要变成找比k大的了，而且要从前往后找了。递加变量i，发现下标2的数据是第一个比k大的，于是用下标2的数据7和j指向的下标3的数据的6做交换，数据状态变成下表：
i=2 j=3 k=6
称上面两次比较为一个循环。
接着，再递减变量j，不断重复进行上面的循环比较。
在本例中，我们进行一次循环，就发现i和j“碰头”了：他们都指向了下标2。于是，第一遍比较结束。得到结果如下，凡是k(=6)左边的数都比它小，凡是k右边的数都比它大：
如果i和j没有碰头的话，就递加i找大的，还没有，就再递减j找小的，如此反复，不断循环。注意判断和寻找是同时进行的。
然后，对k两边的数据，再分组分别进行上述的过程，直到不能再分组为止。
注意：第一遍快速排序不会直接得到最终结果，只会把比k大和比k小的数分到k的两边。为了得到最后结果，需要再次对下标2两边的数组分别执行此步骤，然后再分解数组，直到数组不能再分解为止（只有一个数据），才能得到正确结果。
#_*_coding:utf-8_*_
__author__ = 'Alex Li'
def quick_sort(array,left,right):
'''
:param array:
:param left: 列表的第一个索引
:param right: 列表最后一个元素的索引
:return:
'''
if left >=right:
return
low = left
high = right
key = array[low] #第一个值
while low < high:#只要左右未遇见
while low < high and array[high] > key: #找到列表右边比key大的值 为止
high -= 1
#此时直接 把key(array[low]) 跟 比它大的array[high]进行交换
array[low] = array[high]
array[high] = key
while low < high and array[low] <= key : #找到key左边比key大的值，这里为何是<=而不是<呢？你要思考。。。
low += 1
#array[low] =
#找到了左边比k大的值 ,把array[high](此时应该刚存成了key) 跟这个比key大的array[low]进行调换
array[high] = array[low]
array[low] = key
quick_sort(array,left,low-1) #最后用同样的方式对分出来的左边的小组进行同上的做法
quick_sort(array,low+1, right)#用同样的方式对分出来的右边的小组进行同上的做法
if __name__ == '__main__':
array = [96,14,10,9,6,99,16,5,1,3,2,4,1,13,26,18,2,45,34,23,1,7,3,22,19,2]
#array = [8,4,1, 14, 6, 2, 3, 9,5, 13, 7,1, 8,10, 12]
print("before sort:", array)
quick_sort(array,0,len(array)-1)
print("-------final -------")
print(array)登入後複製
二叉树
树的特征和定义
树是一种重要的非线性数据结构，直观地看，它是数据元素（在树中称为结点）按分支关系组织起来的结构，很象自然界中的树那样。树结构在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构都可用树形象表示。树在计算机领域中也得到广泛应用，如在编译源程序时，可用树表示源程序的语法结构。又如在数据库系统中，树型结构也是信息的重要组织形式之一。一切具有层次关系的问题都可用树来描述。
树(Tree)是元素的集合。我们先以比较直观的方式介绍树。下面的数据结构是一个树：
树有多个节点(node)，用以储存元素。某些节点之间存在一定的关系，用连线表示，连线称为边(edge)。边的上端节点称为父节点，下端称为子节点。树像是一个不断分叉的树根。
每个节点可以有多个子节点(children)，而该节点是相应子节点的父节点(parent)。比如说，3,5是6的子节点，6是3,5的父节点；1,8,7是3的子节点, 3是1,8,7的父节点。树有一个没有父节点的节点，称为根节点(root)，如图中的6。没有子节点的节点称为叶节点(leaf)，比如图中的1,8,9,5节点。从图中还可以看到，上面的树总共有4个层次，6位于第一层，9位于第四层。树中节点的最大层次被称为深度。也就是说，该树的深度(depth)为4。
如果我们从节点3开始向下看，而忽略其它部分。那么我们看到的是一个以节点3为根节点的树：
三角形代表一棵树
再进一步，如果我们定义孤立的一个节点也是一棵树的话，原来的树就可以表示为根节点和子树(subtree)的关系:
上述观察实际上给了我们一种严格的定义树的方法：
1. 树是元素的集合。
2. 该集合可以为空。这时树中没有元素，我们称树为空树 (empty tree)。
3. 如果该集合不为空，那么该集合有一个根节点，以及0个或者多个子树。根节点与它的子树的根节点用一个边(edge)相连。
上面的第三点是以递归的方式来定义树，也就是在定义树的过程中使用了树自身(子树)。由于树的递归特征，许多树相关的操作也可以方便的使用递归实现。我们将在后面看到。
树的实现
樹的示意圖已經給出了樹的一種記憶體實現方式: 每個節點儲存元素和多個指向子節點的指標。然而，子節點數目是不確定的。一個父節點可能有大量的子節點，而另一個父節點可能只有一個子節點，而樹的增刪節點操作會讓子節點的數目有進一步的變化。這種不確定性可能會帶來大量的記憶體相關操作，並且容易造成記憶體的浪費。
一種經典的實作方式如下:
#樹的記憶體實作
擁有同一父節點的兩個節點互為兄弟節點(sibling)。上圖的實作方式中，每個節點包含一個指標指向第一個子節點，並有另一個指標指向它的下一個兄弟節點。這樣，我們就可以用統一的、確定的結構來表示每個節點。
電腦的檔案系統是樹的結構，例如Linux檔案管理背景知識中所介紹的。在UNIX的檔案系統中，每個檔案(資料夾同樣是一種檔案)，都可以看做是一個節點。非資料夾的檔案被儲存在葉節點。資料夾中有指向父節點和子節點的指針(在UNIX中，資料夾還包含一個指向自身的指針，這與我們上面見到的樹有所區別)。在git中，也有類似的樹狀結構，用以表達整個檔案系統的版本變化 (參考版本管理三國誌)。
二元樹：
二元樹是由n（n≥0）個結點組成的有限集合、每個結點最多有兩個子樹的有序樹。它或是空集，或是由兩個根和稱為左、右子樹的兩個不相交的二元樹組成。
特點：
（1）二元樹是有序樹，即使只有一個子樹，也必須區分左、右子樹；
（2）二元樹的每個結點的度不能大於2，只能取0、1、2三者之一；
（3）二元樹中所有結點的形態有5種：空結點、無左右子樹的結點、只有左子樹的結點、只有右子樹的結點和具有左右子樹的結點。
二元樹(binary)是一種特殊的樹。二元樹的每個節點最多只能有2個子節點：
二元樹
由於二元樹的子節點數目確定，所以可以直接採用上圖方式在記憶體中實現。每個節點有一個左子節點(left children)和右子節點(right children)。左子節點是左子樹的根節點，右子節點是右子樹的根節點。
如果我們為二元樹加一個額外的條件，就可以得到一種被稱為二元搜尋樹(binary search tree)的特殊二元樹。二元搜尋樹需求：每個節點都不比它左子樹的任意元素小，而且不比它的右子樹的任意元素大。
(如果我們假設樹中沒有重複的元素，那麼上述要求可以寫成：每個節點比它左子樹的任意節點大，而且比它右子樹的任意節點小)
二元搜尋樹，注意樹中元素的大小
#二元搜尋樹可以方便的實作搜尋演算法。在搜尋元素x的時候，我們可以將x和根節點比較:
1. 如果x等於根節點，那麼找到x，停止搜尋(終止條件)
2. 如果x小於根節點，那麼搜尋左子樹
3. 如果x大於根節點，那麼搜尋右子樹
二元搜尋樹所需要進行的操作次數最多與樹的深度相等。 n個節點的二元搜尋樹的深度最多為n，最少為log(n)。
二元樹的遍歷
遍歷即將樹的所有結點存取且僅存取一次。依根節點位置的不同分為前序遍歷，中序遍歷，後序遍歷。
前序遍歷：根節點->左子樹->右子樹
#中序遍歷：左子樹->根節點->右子樹
後序遍歷：左子樹->右子樹->根節點
#例如：求下面樹的三種遍歷
前序遍歷：abdefgc
中序遍歷：debgfac
#後序遍歷：edgfbca
二元樹的類型
(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。
(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树
如何判断一棵树是完全二叉树？按照定义
教材上的说法：一个深度为k，节点个数为 2^k - 1 的二叉树为满二叉树。这个概念很好理解，就是一棵树，深度为k，并且没有空位。
首先对满二叉树按照广度优先遍历（从左到右）的顺序进行编号。
一颗深度为k二叉树，有n个节点，然后，也对这棵树进行编号，如果所有的编号都和满二叉树对应，那么这棵树是完全二叉树。
如何判断平衡二叉树？
（b）左边的图 左子数的高度为3，右子树的高度为1，相差超过1
（b）右边的图 -2的左子树高度为0 右子树的高度为2，相差超过1
二叉树遍历实现
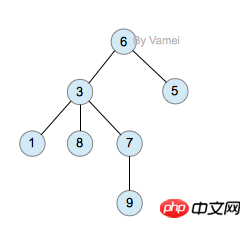
class TreeNode(object):
def __init__(self,data=0,left=0,right=0):
self.data = data
self.left = left
self.right = right
class BTree(object):
def __init__(self,root=0):
self.root = root
def preOrder(self,treenode):
if treenode is 0:
return
print(treenode.data)
self.preOrder(treenode.left)
self.preOrder(treenode.right)
def inOrder(self,treenode):
if treenode is 0:
return
self.inOrder(treenode.left)
print(treenode.data)
self.inOrder(treenode.right)
def postOrder(self,treenode):
if treenode is 0:
return
self.postOrder(treenode.left)
self.postOrder(treenode.right)
print(treenode.data)
if __name__ == '__main__':
n1 = TreeNode(data=1)
n2 = TreeNode(2,n1,0)
n3 = TreeNode(3)
n4 = TreeNode(4)
n5 = TreeNode(5,n3,n4)
n6 = TreeNode(6,n2,n5)
n7 = TreeNode(7,n6,0)
n8 = TreeNode(8)
root = TreeNode('root',n7,n8)
bt = BTree(root)
print("preOrder".center(50,'-'))
print(bt.preOrder(bt.root))
print("inOrder".center(50,'-'))
print (bt.inOrder(bt.root))
print("postOrder".center(50,'-'))
print (bt.postOrder(bt.root))登入後複製
堆排序
堆排序，顾名思义，就是基于堆。因此先来介绍一下堆的概念。
堆分为最大堆和最小堆，其实就是完全二叉树。最大堆要求节点的元素都要大于其孩子，最小堆要求节点元素都小于其左右孩子，两者对左右孩子的大小关系不做任何要求，其实很好理解。有了上面的定义，我们可以得知，处于最大堆的根节点的元素一定是这个堆中的最大值。其实我们的堆排序算法就是抓住了堆的这一特点，每次都取堆顶的元素，将其放在序列最后面，然后将剩余的元素重新调整为最大堆，依次类推，最终得到排序的序列。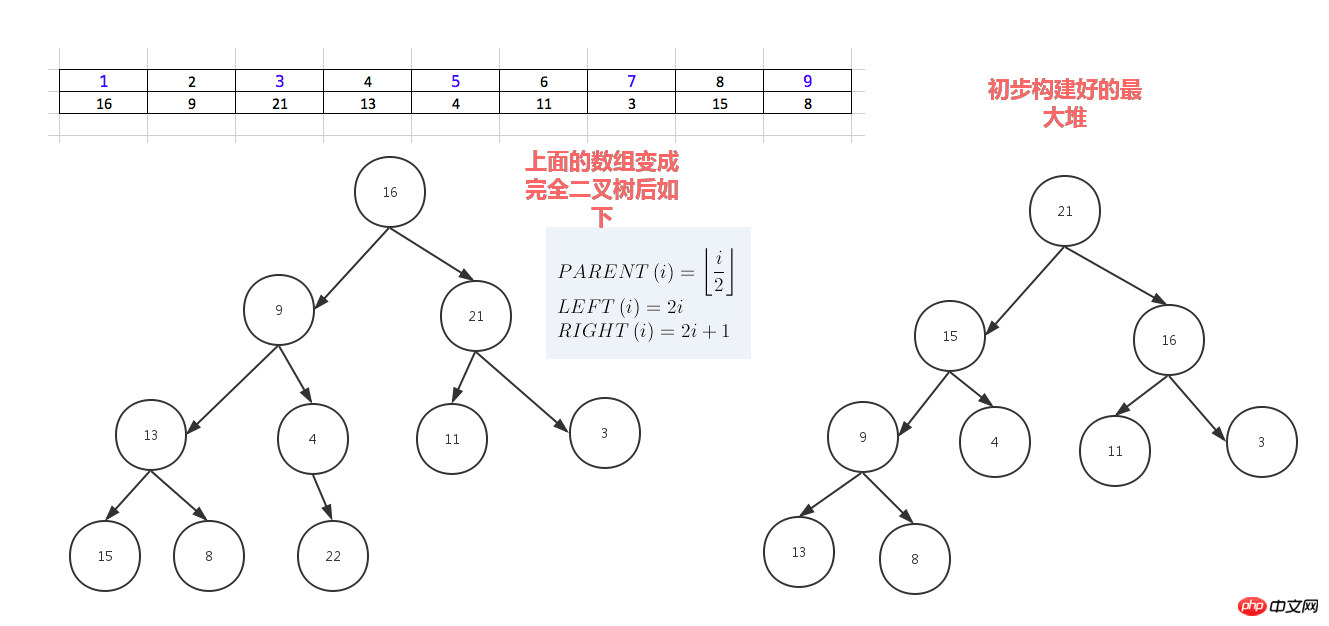
堆排序就是把堆顶的最大数取出,
将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现
剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束
#_*_coding:utf-8_*_
__author__ = 'Alex Li'
import time,random
def sift_down(arr, node, end):
root = node
#print(root,2*root+1,end)
while True:
# 从root开始对最大堆调整
child = 2 * root +1 #left child
if child > end:
#print('break',)
break
print("v:",root,arr[root],child,arr[child])
print(arr)
# 找出两个child中交大的一个
if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
child += 1 #设置右边为大
if arr[root] < arr[child]:
# 最大堆小于较大的child, 交换顺序
tmp = arr[root]
arr[root] = arr[child]
arr[child]= tmp
# 正在调整的节点设置为root
#print("less1:", arr[root],arr[child],root,child)
root = child #
#[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
#print("less2:", arr[root],arr[child],root,child)
else:
# 无需调整的时候, 退出
break
#print(arr)
print('-------------')
def heap_sort(arr):
# 从最后一个有子节点的孩子还是调整最大堆
first = len(arr) // 2 -1
for i in range(first, -1, -1):
sift_down(arr, i, len(arr) - 1)
#[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
print('--------end---',arr)
# 将最大的放到堆的最后一个, 堆-1, 继续调整排序
for end in range(len(arr) -1, 0, -1):
arr[0], arr[end] = arr[end], arr[0]
sift_down(arr, 0, end - 1)
#print(arr)
def main():
# [7, 95, 73, 65, 60, 77, 28, 62, 43]
# [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
#l = [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
#l = [16,9,21,13,4,11,3,22,8,7,15,27,0]
array = [16,9,21,13,4,11,3,22,8,7,15,29]
#array = []
#for i in range(2,5000):
# #print(i)
# array.append(random.randrange(1,i))
print(array)
start_t = time.time()
heap_sort(array)
end_t = time.time()
print("cost:",end_t -start_t)
print(array)
#print(l)
#heap_sort(l)
#print(l)
if __name__ == "__main__":
main()登入後複製
人类能理解的版本
dataset = [16,9,21,3,13,14,23,6,4,11,3,15,99,8,22]
for i in range(len(dataset)-1,0,-1):
print("-------",dataset[0:i+1],len(dataset),i)
#for index in range(int(len(dataset)/2),0,-1):
for index in range(int((i+1)/2),0,-1):
print(index)
p_index = index
l_child_index = p_index *2 - 1
r_child_index = p_index *2
print("l index",l_child_index,'r index',r_child_index)
p_node = dataset[p_index-1]
left_child = dataset[l_child_index]
if p_node < left_child: # switch p_node with left child
dataset[p_index - 1], dataset[l_child_index] = left_child, p_node
# redefine p_node after the switch ,need call this val below
p_node = dataset[p_index - 1]
if r_child_index < len(dataset[0:i+1]): #avoid right out of list index range
#if r_child_index < len(dataset[0:i]): #avoid right out of list index range
#print(left_child)
right_child = dataset[r_child_index]
print(p_index,p_node,left_child,right_child)
# if p_node < left_child: #switch p_node with left child
# dataset[p_index - 1] , dataset[l_child_index] = left_child,p_node
# # redefine p_node after the switch ,need call this val below
# p_node = dataset[p_index - 1]
#
if p_node < right_child: #swith p_node with right child
dataset[p_index - 1] , dataset[r_child_index] = right_child,p_node
# redefine p_node after the switch ,need call this val below
p_node = dataset[p_index - 1]
else:
print("p node [%s] has no right child" % p_node)
#最后这个列表的第一值就是最大堆的值，把这个最大值放到列表最后一个， 把神剩余的列表再调整为最大堆
print("switch i index", i, dataset[0], dataset[i] )
print("before switch",dataset[0:i+1])
dataset[0],dataset[i] = dataset[i],dataset[0]
print(dataset)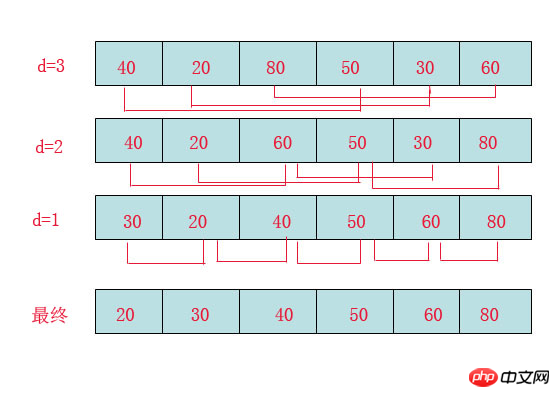登入後複製
希尔排序（shell sort）
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本,该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高
首先要明确一下增量的取法：
第一次增量的取法为： d=count/2;
第二次增量的取法为: d=(count/2)/2;
最后一直到: d=1;
看上图观测的现象为：
d=3时：将40跟50比，因50大，不交换。
将20跟30比，因30大，不交换。
将80跟60比，因60小，交换。
d=2时：将40跟60比，不交换，拿60跟30比交换，此时交换后的30又比前面的40小，又要将40和30交换，如上图。
将20跟50比，不交换，继续将50跟80比，不交换。
d=1时：这时就是前面讲的插入排序了，不过此时的序列已经差不多有序了，所以给插入排序带来了很大的性能提高。
希尔排序代码
import time,random
#source = [8, 6, 4, 9, 7, 3, 2, -4, 0, -100, 99]
#source = [92, 77, 8,67, 6, 84, 55, 85, 43, 67]
source = [ random.randrange(10000+i) for i in range(10000)]
#print(source)
step = int(len(source)/2) #分组步长
t_start = time.time()
while step >0:
print("---step ---", step)
#对分组数据进行插入排序
for index in range(0,len(source)):
if index + step < len(source):
current_val = source[index] #先记下来每次大循环走到的第几个元素的值
if current_val > source[index+step]: #switch
source[index], source[index+step] = source[index+step], source[index]
step = int(step/2)
else: #把基本排序好的数据再进行一次插入排序就好了
for index in range(1, len(source)):
current_val = source[index] # 先记下来每次大循环走到的第几个元素的值
position = index
while position > 0 and source[
position - 1] > current_val: # 当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
source[position] = source[position - 1] # 把左边的一个元素往右移一位
position -= 1 # 只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止
source[position] = current_val # 已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
print(source)
t_end = time.time() - t_start
print("cost:",t_end)登入後複製
以上是Python中基本且又常用的演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章！
