Mahout提供一些可擴展的機器學習領域經典演算法的實現,旨在幫助開發人員更方便快速地創建智慧應用程式。 Mahout包含許多實現,包括聚類、分類、建議過濾、頻繁子項挖掘。此外,透過使用 Apache Hadoop 函式庫,Mahout 可以有效地擴展到雲端。

該老師講課風格:
#教師講課深入淺出,條理清楚,層層剖析,環環相扣,論證嚴密,結構嚴謹,用思考的邏輯力量吸引學生的注意力,用理智控制課堂教學進程。學生透過聽教師的講授,不僅學到知識,也受到思維的訓練,還受到教師嚴謹的治學態度的熏陶和感染
本視頻中較為難點是邏輯回歸分類器_貝葉斯分類器_1了:
1.背景
首先,在文章的開頭,先提出幾個問題,如果這些問題你都答得上來,那麼本文你就無需閱讀了,或者你閱讀的動機純粹是給本文挑毛病,當然我也無比歡迎,請發送郵件“毛病の樸素貝葉斯”發送至297314262 @qq.com,我會認真閱讀你的來信。
By the way,如果閱讀完本文,你還是無法回答以下問題,那麼也請你電子郵件通知我,我會盡量解答你的疑惑。
樸素貝葉斯分類器中的「樸素」特別指此分類器的什麼特性
樸素貝葉斯分類器與極大似然估計(MLE)、最大後驗機率(MAP)的關係
樸素貝葉斯分類、邏輯迴歸分類,產生模型、判決模型的關係
有監督學習和貝葉斯估計的關係
2.約定
那麼,本文開始。首先,關於本文可能出現的各種表達形式,在此做一番約定
大寫字母,如X,表示隨機變量;如果X是多維變量,那麼下標i表示第i維變量,即Xi
小寫字母,如Xij,表示變數的一種取值(Xi的第j種取值)
3.貝葉斯估計與有監督學習
好的,那麼先回答第4個問題,如何用貝葉斯估計解決有監督學習問題?
對於有監督學習,我們的目標實際上是估計一個目標函數f : X->Y,,或目標分佈P(Y|X),其中X是樣本的各個feature組成的多維變量,Y是樣本的實際分類結果。假設樣本X的取值為xk,那麼,根據貝葉斯定理,分類結果為yi的機率應該是:
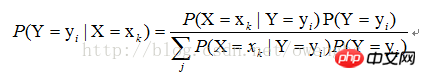
因此,要估計P(Y=yi |X=xk),只要根據樣本,求P(X=xk|Y=yi)的所有估計,以及P(Y=yi)的所有估計,就可以了。此後的分類過程,就是求另P(Y=yi|X=xk)最大的那個yi就可以了。那麼由此可見,利用貝葉斯估計,可以解決監督學習的問題。
4.分類器的「樸素」特性
接下來,回答第1個問題,何為「樸素」?
從第3節的分析裡,我們知道,要求得到P(Y=yi|X=xk),就需要知道P(X=xk|Y=yi)的所有估計,以及P( Y=yi)的所有估計,那麼假設X為N維變量,其每一維變量都有兩種取值(如文本分類中常見的各個term出現與否對應的取值0/1),而Y也有兩種類別,那麼就需要求出2*(2^N - 1)個估計值(注意,由於在給定Y為某一類別的情況下,X的各個取值的機率和為1,所以實際需要估計的值為2^N - 1)。可以想像,對於N很大的情況(文字分類時,term的可能取值是非常大的),這一估計的計算量是巨大的。那麼如何減少需要估計的量,而使得貝葉斯估計方法具有可行性呢?這裡,就引入一個假設:
假設:在給定Y=yi的條件下,X的各維變數彼此互相獨立。
那麼,在這假設的條件下,P(X=xk|Y=yi)=P(X1=x1j1|Y=yi)P(X2=x2j2|Y=yi)... P(Xn=xnjn|Y=yi),也就是說,此時只需要求出N個估計就可以了。因此,這個假設將貝葉斯估計的計算量從2*(2^N - 1)降為了N,使此分類器具有了實際可行性。那麼這個假設就成為樸素特性。
5.極大似然估計和最大後驗機率解
接下來,回答第2個問題,首選我們將極大似然估計法應用於樸素貝葉斯分類器的求解過程。
上面說了,P(X=xk|Y=yi)的求解,可以轉換成對P(X1=x1j1|Y=yi)、P(X2=x2j2|Y=yi)、... P (Xn=xnjn|Y=yi)的求解,那麼如何用極大似然估計法來求這些值呢?
首選我們需要理解什麼是極大似然估計,實際上,在我們的概率論課本里,關於極大似然估計的講解,都是在解決無監督學習問題,而看完本節內容後,你應該明白,在樸素特性下,用極大似然估計解決有監督學習問題,實際上就是在各個類別的條件下,用極大似然估計解決無監督學習問題。
以上是Mahout影片教學的資源推薦的詳細內容。更多資訊請關注PHP中文網其他相關文章!




