js實作資料結構: 樹和二元樹,二元樹的遍歷和基本操作方法

樹型結構是一類非常重要的非線性結構。直觀地，樹型結構是以分支關係定義的層次結構。

樹在電腦領域中也有廣泛的應用，例如在編譯程式中，用樹來表示​​原始程式的語法結構；在資料庫系統中，可用樹來組織資訊；在分析演算法的行為時，可用樹來描述其執行過程等等

#首先看看樹的一些概念：1.樹（Tree）是n（n>=0）個結點的有限集合。在任一非空樹中：

　　（1）有且僅有一個特定的稱為根（Root）的結點；

　　（2）當n>1時，其餘結點可分為m(m>0)個互不相交的有限集合T1,T2,T3,…Tm，其中每一個集合本身又是一棵樹，並且稱為根的子樹（Subtree）。

例如，（a）是只有一個根結點的樹；（b）是有13個結點的樹，其中A是根，其餘結點分成3個互不相交的子集： T1={B,E,F,K,L},t2={D,H,I,J,M};T1,T2和T3都是根A的子樹，本身也是一棵樹。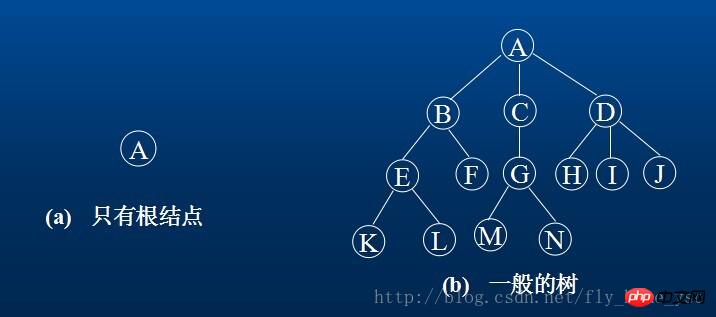

2.樹的結點包含一個資料元素及若干指向其子樹的分支。結點擁有的子樹數稱為結點的度數（Degree）。例如，（b）中A的度數為3，C的度數為1，F的度數為0.度為0的結點稱為葉子（Leaf）或終端結點。度不為0的結點稱為非終端結點或分支結點。樹的度數是樹內各結點的度數的最大值。 （b）的樹的度為3.結點的子樹的根稱為該結點的孩子（Child）。相應的，該結點稱為孩子的雙親（Parent）。同一個雙親的孩子之間互稱兄弟（Sibling）。結點的祖先是從根到該結點所經分支上的所有結點。反之，以某結點為根的子樹中的任一結點稱為該結點的子孫。

3.結點的層次（Level）從根開始定義起，根為第一層，跟的孩子為第二層。若某結點在第l層，則其子樹的根就在第l+1層。其雙親在同一層的結點互為堂兄弟。例如，結點G與E，F,H,I,J互為堂兄弟。樹中結點的最大層次稱為樹的深度（Depth）或高度。 （b）的樹的深度為4。

4.如果將樹中結點的各子樹看成從左到右是有次序的（即不能交換），則稱該樹為有序樹，否則稱為無序樹。在有序樹中最左邊的子樹的根稱為第一個孩子，最右邊的稱為最後一個孩子。

5.森林（Forest）是m（m>=0）棵互不相交的樹的集合。對樹中每個結點而言，其子樹的集合即為森林。

接下來看看二元樹相關的概念：

二元樹（Binary Tree）是另一個樹型結構，它的特徵是每個結點至多只有兩棵子樹（即二元樹中不存在度大於2的結點），並且，二叉樹的子樹有左右之分（其次序不能任意顛倒。）

二叉樹的性質：

　　1.在二叉樹的第i層上至多有2的i-1次方個結點(i>=1)。

　　2.深度為k的二元樹至多有2的k次方-1個結點，(k>=1)。

　　3.對任何一棵二元樹T，若其終端結點數為n0，度為2的結點數為n2，則n0 = n2 + 1;

#　　　　一棵深度為k且有2的k次方-1個結點的二元樹稱為滿叉樹。

　　　　深度為k的，有n個結點的二元樹，當且僅當其每一個結點都與深度為k的滿二叉樹中編號從1至n的結點一一對應時，稱為完全二元樹。

下面是完全二元樹的兩個特性：

　　4.具有n個結點的完全二元樹的深度為Math.floor(log 2 n) + 1

5.如果將一棵有n個結點的完全二元樹（其深度為Math.floor(log 2 n) + 1）的結點按層序編號（從第1層到第Math.floor(2 n) + 1，每層由左至右），則對任一結點（1

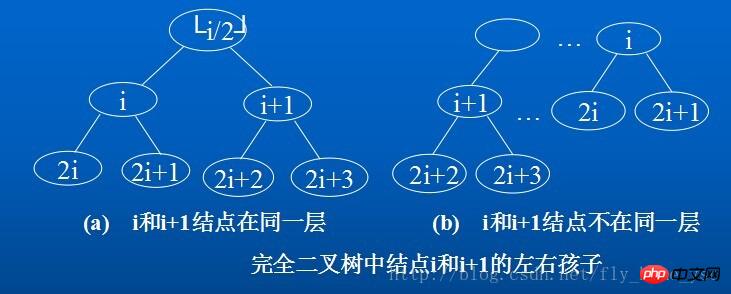
　　　　(1)如果i=1，則結點i、是二叉樹的根，無雙親；如果i>1，則其雙親parent(i)是結點Math.floor(i/2)。

　　　　(2)如果2i > n，則結點i無左孩子（結點i為葉子結點）；否則其左孩子LChild(i)是結點2i.

#　　　　(3)如果2i + 1 > n，則結點i無右孩子；否則其右孩子RChild(i)是結點2i + 1;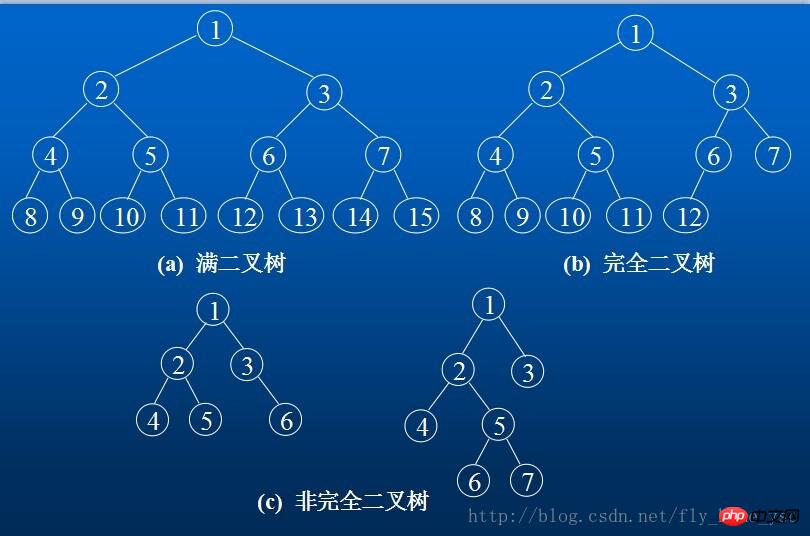

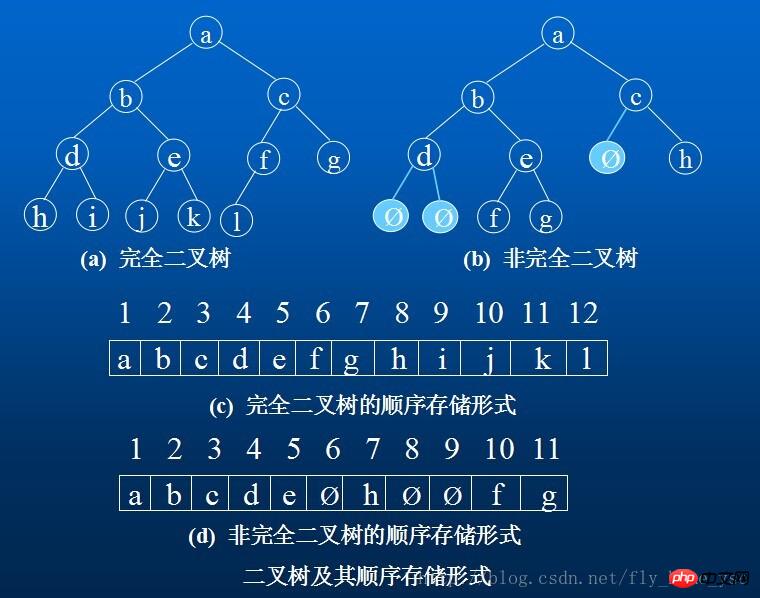
############################################################ ######二元樹的儲存結構###

1.順序儲存結構
用一組連續的儲存單元依序自上而下，自左至右儲存完全二元樹上的結點元素，即將二叉樹上編號為i的結點元素儲存在加上定義的一維數組中下標為i-1的分量中。 「0」表示不存在此結點。這種順序存儲結構僅適用於完全二元樹。
因為，在最壞情況下，一個深度為k且只有k個結點的單支樹（樹中不存在度為2的結點）卻需要長度為2的n次方-1的一維數組。

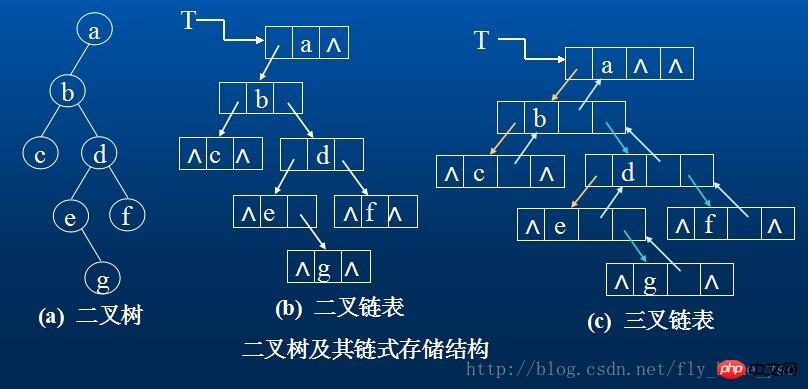
2.鍊式儲存結構
二元樹的結點由一個資料元素和分別指向其左右子樹的兩個分支構成，則表示二元樹的鍊錶中的結點至少包含三個域：資料域和左右指標域。有時，為了便於找到結點的雙親，則還可在結點結構中增加一個指向其雙親結點的指標域。利用這兩種結構所得的二元樹的儲存結構分別稱之為二元鍊錶和三叉鍊錶。
在含有n個結點的二叉鍊錶中有n+1個空鏈域，我們可以利用這些空鏈域存儲其他有用信息，從而得到另一種鍊式存儲結構—線索鍊錶。

二元樹的遍歷主要分為三種：

先（根）序遍歷：根左右
中（根）序遍歷：左根右
後（根）序遍歷：左右根

二元樹的順序儲存結構：

#二元樹的鍊式儲存形式：

// 顺序存储结构
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];
    // 链式存储结构
    function BinaryTree(data, leftChild, rightChild) {
        this.data = data || null;
        // 左右孩子结点
        this.leftChild = leftChild || null;
        this.rightChild = rightChild || null;
    }

遍歷二元樹(Traversing Binary Tree)：是指依照指定的規律對二元樹中的每個結點存取一次且僅造訪一次。

1.先序遍歷二元樹

1)演算法的遞歸定義是：

　　若二叉樹為空，則遍歷結束；否則

　　⑴ 訪問根結點;

　　⑵ 先序遍歷左子樹(遞歸呼叫本演算法);<br/>

　　⑶ 先序遍歷右子樹(遞歸呼叫本演算法)。

演算法實作：###

// 顺序存储结构的递归先序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    console.log('preOrder:');
    void function preOrderTraverse(x, visit) {
        visit(tree[x]);
        if (tree[2 * x + 1]) preOrderTraverse(2 * x + 1, visit);
        if (tree[2 * x + 2]) preOrderTraverse(2 * x + 2, visit);
    }(0, function (value) {
        console.log(value);
    });
    // 链式存储结构的递归先序遍历
    BinaryTree.prototype.preOrderTraverse = function preOrderTraverse(visit) {
        visit(this.data);
        if (this.leftChild) preOrderTraverse.call(this.leftChild, visit);
        if (this.rightChild) preOrderTraverse.call(this.rightChild, visit);
    };

###2)非遞迴演算法:######設T是指向二元樹根結點的變量，非遞歸演算法是： 若二元樹為空，則返回；否則，令p=T;######　　(1) p為根結點；######　　(2) 若p不為空或堆疊不為空；###### (3) 若p不為空，訪問p所指向的結點, p進棧, p = p.leftChild，訪問左子樹；######　　　　(4) 否則；退棧到p，然後p = p.rightChild, 訪問右子樹######　　(5) 轉(2)，直到棧空為止。 ######程式碼實作：###

// 链式存储的非递归先序遍历

    // 方法1
    BinaryTree.prototype.preOrder_stack = function (visit) {        
    var stack = new Stack();        
    stack.push(this);        
    while (stack.top) {            
    var p;            // 向左走到尽头
            while ((p = stack.peek())) {
                p.data && visit(p.data);                
                stack.push(p.leftChild);
            }            
            stack.pop();            
            if (stack.top) {
                p = stack.pop();                
                stack.push(p.rightChild);
            }
        }
    };    // 方法2
     BinaryTree.prototype.preOrder_stack2 = function (visit) {        
     var stack = new Stack();        
     var p = this;        
     while (p || stack.top) {            
     if (p) {                
     stack.push(p);
                p.data && visit(p.data);
                p = p.leftChild;
            } else {
                p = stack.pop();
                p = p.rightChild;
            }
        }
    };

###2.中序遍歷二元樹：######1）演算法的遞歸定義為：######　　若二元樹為空，則遍歷結束；否則######　　⑴ 中序遍歷左子樹(遞歸調用本演算法);######　　⑵ 存取根結點；######　　⑶ 中序歸來右子樹(遞歸調用本演算法)。 ###

// 顺序存储结构的递归中序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    
    console.log('inOrder:');
    void function inOrderTraverse(x, visit) {        
    if (tree[2 * x + 1]) inOrderTraverse(2 * x + 1, visit);
        visit(tree[x]);
        if (tree[2 * x + 2]) inOrderTraverse(2 * x + 2, visit);
    }(0, function (value) {
        console.log(value);
    });

    // 链式存储的递归中序遍历
    BinaryTree.prototype.inPrderTraverse = function inPrderTraverse(visit) {        
    if (this.leftChild) inPrderTraverse.call(this.leftChild, visit);
        visit(this.data);
        if (this.rightChild) inPrderTraverse.call(this.rightChild, visit);
    };

###2) 非遞歸演算法######　　T是指向二元樹根結點的變量，非遞歸演算法是： 若二元樹為空，則傳回；否則，令p=T### ###　　⑴ 若p不為空，p進棧， p=p.leftChild ;###

<br/>

###　　⑵ 否則(即p為空)，退棧到p，訪問p所指向的結點，p =p.rightChild ;######　　⑶ 轉(1);######　　直到棧空為止。 ###　　###

// 方法1
    inOrder_stack1: function (visit) {        
    var stack = new Stack();        
    stack.push(this);        
    while (stack.top) {            
    var p;            // 向左走到尽头
            while ((p = stack.peek())) {                
            stack.push(p.leftChild);
            }            
            stack.pop();            
            if (stack.top) {
                p = stack.pop();
                p.data && visit(p.data);                
                stack.push(p.rightChild);
            }
        }
    },    // 方法2
    inOrder_stack2: function (visit) {        
    var stack = new Stack();        
    var p = this;        
    while (p || stack.top) {            
    if (p) {                
    stack.push(p);
                p = p.leftChild;
            } else {
                p = stack.pop();
                p.data && visit(p.data);
                p = p.rightChild;
            }
        }
    },

###3.後序遍歷二叉樹:######1)遞歸演算法######　　若二叉樹為空，則遍歷結束；否則######　　⑴後序遍歷左子樹(遞歸呼叫本演算法);######　　⑵ 後序遍歷右子樹(遞歸呼叫本演算法) ;######　　⑶ 存取根結點。 ######

// 顺序存储结构的递归后序遍历
    var tree = [1, 2, 3, 4, 5, , 6, , , 7];    
    console.log('postOrder:');
    void function postOrderTraverse(x, visit) {        
    if (tree[2 * x + 1]) postOrderTraverse(2 * x + 1, visit);
        if (tree[2 * x + 2]) postOrderTraverse(2 * x + 2, visit);
        visit(tree[x]);
    }(0, function (value) {
        console.log(value);
    });
    // 链式存储的递归后序遍历
    BinaryTree.prototype.postOrderTraverse = function postOrderTraverse(visit) {        
    if (this.leftChild) postOrderTraverse.call(this.leftChild, visit);
        if (this.rightChild) postOrderTraverse.call(this.rightChild, visit);
        visit(this.data);
    };

###2) 非遞迴演算法######在後序遍歷中，根結點是最後被存取的。因此，在遍歷過程中，當搜尋指標指向某根結點時，不能立即訪問，而要先遍歷其左子樹，此時根結點進棧。當其左子樹遍歷完後再搜尋到該根結點時，還是不能訪問，還需遍歷其右子樹。所以，此根結點還需再次進棧，當其右子樹遍歷完後再退棧到到該根結點時，才能被存取。 因此，設立一個狀態標誌變數mark：######　  mark=0表示剛剛訪問此結點，mark=1表示左子樹處理結束返回，######　　mark=2表示右子樹處理結束返回。每次根據棧頂的mark域決定要做何動作######演算法實作想法：######　　(1) 根結點入棧，且mark = 0;######　　(2 ) 若堆疊不為空，出棧到node；######　　　　(3) 若node的mark = 0，修改當前node的mark為1，左子樹入堆疊；######　　　　(4 ) 若node的mark = 1，修改目前的nodemark為2，右子樹入堆疊；######　　　　(5) 若node的mark = 2，存取目前node結點的值；#### ##　　(6) 直到堆疊為空結束。 ###　　###

postOrder_stack: function (visit) {
        var stack = new Stack();        
        stack.push([this, 0]);        
        while (stack.top) {
            var a = stack.pop();
            var node = a[0];            
            switch (a[1]) {                
            case 0:                    
            stack.push([node, 1]);  // 修改mark域
                    if (node.leftChild) stack.push([node.leftChild, 0]);  // 访问左子树
                    break;                
                    case 1:                    
                    stack.push([node, 2]);                    
                    if (node.rightChild) stack.push([node.rightChild, 0]);                    
                    break;                
                    case 2:
                    node.data && visit(node.data);                    
                    break;                
                    default:                    
                    break;
            }
        }
    }

###具體的一個例子###

<html>
  <head>
    <meta charset="utf-8">
    <title>文档标题</title>
    <meta http-equiv="X-UA-Compatible" content="IE=edge,chrome=1" />
    <meta name="renderer" content="webkit">
    <meta name="keywords" content="your keywords">
    <meta name="description" content="your description">
    <link rel="shortcut icon" type="image/ico" href="/favicon.ico" />
    <meta name="viewport" content="width=device-width, initial-scale=1.0"></head><body>
    <p class="container"></p>
    <script>
   // 顺序存储结构
   (function () {
       // 顺序存储结构的遍历
       var tree = ["a","b","c","d","e","f","g"];

       console.log(&#39;preOrder:&#39;);
       +function preOrderTraverse(x, visit) {
           visit(tree[x]);           
           if (tree[2 * x + 1]) preOrderTraverse(2 * x + 1, visit);           
           if (tree[2 * x + 2]) preOrderTraverse(2 * x + 2, visit);
       }(0, function (value) {
           console.log(value);
       });

       console.log(&#39;inOrder:&#39;);       
       void function inOrderTraverse(x, visit) {
           if (tree[2 * x + 1]) inOrderTraverse(2 * x + 1, visit);
           visit(tree[x]);          
           if (tree[2 * x + 2]) inOrderTraverse(2 * x + 2, visit);
       }(0, function (value) {
           console.log(value);
       });

       console.log(&#39;postOrder:&#39;);       
       void function postOrderTraverse(x, visit) {
           if (tree[2 * x + 1]) postOrderTraverse(2 * x + 1, visit);           
           if (tree[2 * x + 2]) postOrderTraverse(2 * x + 2, visit);
           visit(tree[x]);
       }(0, function (value) {
           console.log(value);
       });
   }());   // 求从tree到node结点路径的递归算法
   function findPath(tree, node, path, i) {
       var found = false;       
       void function recurse(tree, i) {
           if (tree == node) {
               found = true;              
               return;
           }

           path[i] = tree;           
           if (tree.leftChild) recurse(tree.leftChild, i + 1);           
           if (tree.rightChild && !found) recurse(tree.rightChild, i + 1);           
           if (!found) path[i] = null;
       }(tree, i);
   }   var global = Function(&#39;return this;&#39;)();    
   </script>
 </body>
</html>

以上是js實作資料結構: 樹和二元樹,二元樹的遍歷和基本操作方法的詳細內容。更多資訊請關注PHP中文網其他相關文章！