有關 PHP 和 js 浮點運算的問題

javascript

0.1 + 0.2 為啥不等於0.3 ?（正確結果：0.30000000000000004）

0.8 * 7 為啥不等於5.6 ?（正確結果：5.6000 ##PHP

var_dump(intval(0.58 * 100));

正確結果是57，而不是58

浮點運算惹的禍

其實這些結果都並非語言的bug，但和語言的實現原理有關， js 所有數字統一為Number, 包括整形實際上全都是雙精度（double）類型。

而PHP會區分 int 還是 float。不管什麼語言，只要牽涉到浮點運算，都是有類似的問題，使用時一定要注意。

浮點二進位原理

根據國際標準IEEE 754，任一二進位浮點數V可以表示成下面的形式：

V = (-1)s * M * E 

    1. (-1)s 表示符号位，当s=0，V为正数；当s=1，V为负数。
    2. M表示有效数字，大于等于1，小于2。
    3. 2E 表示指数位。

舉例來說：十進位的-5.0 ，寫成二進位是-101.0，相當於-1.01×22 。那麼，s=1，M=1.01，E=2。

IEEE 754規定，對於32位的浮點數，最高的1位是符號位s，接著的8位是指數E，剩下的23位為有效數字M。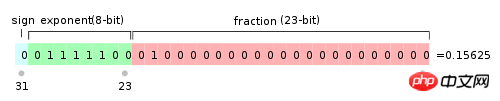

對於64位的浮點數，最高的1位是符號位S，接著的11位是指數E，剩下的52位為有效數字M。

IEEE 754對有效數位M和指數E，還有一些特別規定。

前面說過，1≤M<2，也就是說，M可以寫成1.xxxxxx的形式，其中xxxxxx表示小數部分。 IEEE 754規定，在電腦 內部儲存M時，預設這個數的第一位總是1，因此可以被捨去，只保存後面的xxxxxx部分。例如儲存1.01的時候，只 儲存01，等到讀取的時候，再把第一位的1加上去。這樣做的目的，是節省1位有效數字。以32位浮點數為例，留給 M只有23位，將第一位的1捨去以後，等於可以保存24位有效數字。

至於指數E，情況就比較複雜。

首先，E為一個無符號整數（unsigned int）。這意味著，如果E為8位，它的取值範圍為0~255；如果E為11位，它 的取值範圍為0~2047。但是，我們知道，科學計數法中的E是可以出現負數的，所以IEEE 754規定，E的真實值必須由E再減去一個中間數，對於8位的E，這個中間數是127；對於11位的E，這個中間數是1023。

例如，210 的E是10，所以儲存成32位元浮點數時，必須儲存成10(E的真實值)+127=137(E)，也就是10001001。

然後，指數E還可以再分成三種情況：

（1）E不全為0或不全為1。這時，浮點數就採用上面的規則表示，即指數E的計算值減去127（或1023），得到真實 值，再將有效數字M前加上第一位的1。

（2）E全為0。這時，浮點數的指數E等於1-127（或1-1023），有效數字M不再加上第一位的1，而是還原為 0.xxxxxx的小數。這樣做是為了表示±0，以及接近0的很小的數字。
（3）E全為1。這時，如果有效數字M全為0，表示±無窮大（正負取決於符號位s）；如果有效數字M不全為0，表示 這個數不是一個數（NaN）。 >

以上是有關 PHP 和 js 浮點運算的問題的詳細內容。更多資訊請關注PHP中文網其他相關文章！