其實像在我們前端的開發中，用到的高階演算法不多，大部分情況if語句，for語句，swith語句等等，就可以解決了。稍微複雜的，可能會想到用遞歸的解決。本文主要介紹JavaScript程式設計高階演算法之動態規劃,結合實例形式分析了javascript動態規劃演算法的原理、實作技巧與相關使用注意事項,需要的朋友可以參考下。
但要注意的是遞歸寫起來簡潔，但實際上執行的效率並不高。
我們再看看動態規劃的演算法：
動態規劃解決方案從底部開始解決問題， 將所有小問題解決掉， 然後合併成一個整體解決方案， 從而解決掉整個大問題。
實例舉例 （計算斐波那契數列）
斐波那契數列指的是這樣一個數列1, 1, 2, 3, 5, 8, 13, 21, 34 , 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368........
這個數列從第3項從第3項從第3項從第3項開始，每一項都等於前兩項總和。
針對這個數列，可以用一個遞歸的函數去計算第n項數值
// 斐波那契数列
function recurFib(n) {
if(n < 2){
return n ;
}else {
// document.write("第"+(n-1)+"次计算 n-1="+(n-1)+recurFib(n-1)+' ');
// document.write("n-2="+(n-2)+recurFib(n-2)+"<br>");
return recurFib(n-1)+recurFib(n-2)
}
}確實是非常簡潔的程式碼，上面有被註解的程式碼，是用來印出當n=多少，要執行多少次函數，不過明眼人一眼就能看出來執行的次數隨著n的變大，次數也會非常恐怖增長。
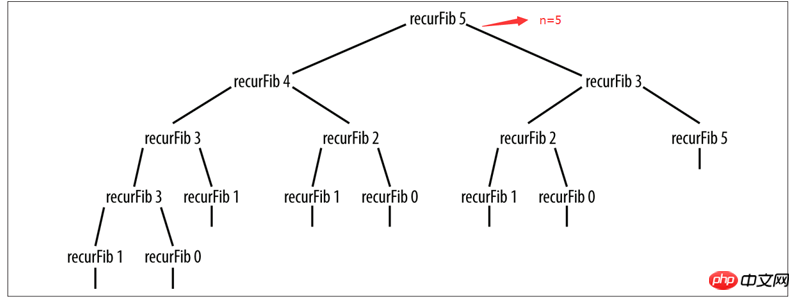
當n=5的時候，遞迴樹已經長的很大了…可以預見當n=10，甚至n=100的時候…
明白了遞迴函數執行效率之差，我們再來看的動態規劃是如何做的
function dynFib(n) {
let val = [];
for(let i = 0; i <= n; ++i){
val[i]=0;
}
if(n ===1 || n === 2){
return 1;
}
else {
val[1] =1;
val[2] = 2;
for(let i = 3; i <= n; ++i){
val[i] = val [i-1] +val[i-2] ;
}
}
return val[n-1]
}透過數組val中保存了中間結果， 如果要計算的斐波那契數是1 或2， 那麼if 語句會回傳1。 否則，數值 1 和 2 將被保存在 val 數組中 1 和 2 的位置。
循環將會從3 到輸入的參數之間進行遍歷， 將數組的每個元素賦值為前兩個元素之和， 循環結束， 數組的最後一個元素值即為最終計算得到的斐波那契數值， 這個數值也會作為函數的回傳值。
接下來可以寫個簡單的測試函數，來比較兩者的運行時間。
// 定义一个测试函数，将待测函数作为参数传入
function test(func,n){
let start = new Date().getTime();//起始时间
let res = func(n);//执行待测函数
document.write('<br>'+'当n='+n+'的时候 '+res+'<br>');
let end = new Date().getTime();//结束时间
return (end - start)+"ms";//返回函数执行需要时间
}列印函數執行
let time = test(recurFib,40); document.write(time); let time2 = test(dynFib,40); document.write(time2);
結果如下：
最後， 你或許已經意識到在使用迭代的方案計算斐波那契數列時， 是可以不使用陣列的。
需要用到陣列的原因是因為動態規劃演算法通常需要保存中間結果。
以下是迭代版本的斐波那契函數義
function iterFib(n) {
let last = 1;
let nextLast = 1;
let result = 1;
for (let i = 2; i < n; ++i) {
result = last + nextLast;
nextLast = last;
last = result;
}
return result;
}當然這個迭代版本的與陣列的版本的效率也是相同的。
相關推薦：
#以上是JavaScript高階演算法動態規劃實例分析的詳細內容。更多資訊請關注PHP中文網其他相關文章！
