人工神經網路是一種模仿動物神經網路行為特徵,進行分散式平行資訊處理的演算法數學模型。這種網路依靠系統的複雜程度,透過調整內部大量節點之間相互連接的關係,從而達到處理資訊的目的,並具有自學習和自適應的能力。本文主要介紹了神經網路理論基礎及Python實現詳解,具有一定藉鏡價值,需要的朋友可以參考下,希望能幫助大家。
一、多層前向神經網路
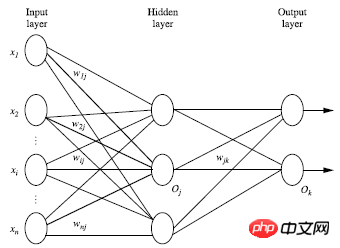
#多層前向神經網路由三個部分組成:輸出層、隱藏層、輸出層,每層由單元組成;
輸入層由訓練集的實例特徵向量傳入,經過連接結點的權重傳入下一層,前一層的輸出是下一層的輸入;隱藏層的數量是任意的,輸入層只有一層,輸出層也只有一層;
除去輸入層之外,隱藏層和輸出層的層數和為n,則該神經網絡稱為n層神經網絡,如下圖為2層的神經網絡;
一層中加權求和,根據非線性方程式進行轉化輸出;理論上,如果有足夠多的隱藏層和足夠大的訓練集,可以模擬任何方程式;
#二、設計神經網路結構
使用在神經網路之前,必須要確定神經網路的層數,以及每層單元的數量;
為了加速學習過程,特徵向量在傳入輸入層前,通常需要標準化到0和1之間;
離散型變數可以被編碼成每個輸入單元對應一個特徵值可能賦的值
例如:特徵值A可能去三個值(a0,a1,a2),則可以使用3個輸入單元來代表A
如果A=a0,則代表a0的單元值取1,其餘取0;
如果A=a1,則代表a1的單元值取1,其餘取0;
如果A=a2,則代表a2的單元值取1,其餘取0;

神經網路既解決分類(classification)問題,也可以解決回歸(regression)問題。對於分類問題,如果是兩類,則可以用一個輸出單元(0和1)分別表示兩類;如果多餘兩類,則每一個類別用一個輸出單元表示,所以輸出層的單元數量通常等一類別的數量。
沒有明確的規則來設計最佳個數的隱藏層,一般根據實驗測試誤差和準確率來改進實驗。
三、交叉驗證方法
如何計算準確率?最簡單的方法是透過一組訓練集和測試集,訓練集透過訓練得到模型,將測試集輸入模型得到測試結果,將測試結果和測試集的真實標籤進行比較,得到準確率。
在機器學習領域常用的方法是交叉驗證方法。一組資料不分成2份,可能分為10份,
第1次:第1份作為測試集,剩餘9份作為訓練集;
第2次:第2份作為測試集,剩餘9份作為訓練集;
……
這樣經過10次訓練,得到10組準確率,將這10組資料求平均值得到平均準確率的結果。這裡10是特例。一般意義上將資料分為k份,稱演算法為K-foldcrossvalidation,即每一次選擇k份中的一份作為測試集,剩餘k-1份作為訓練集,重複k次,最終得到平均準確率,是一種比較科學準確的方法。

四、BP演算法
#透過迭代來處理訓練集中的實例;
比較經過神經網路後預測值與真實值之間的差;
反方向(從輸出層=>隱藏層=>輸入層)來最小化誤差,來更新每個連接的權重;
4.1、演算法詳細介紹
#輸入:資料集、學習率、一個多層神經網路架構;
輸出:一個訓練好的神經網路;
初始化權重與偏向:隨機初始化在-1到1之間(或其他),每個單元都有一個偏向;對於每一個訓練實例X,執行以下步驟:
1、由輸入層向前傳送:
結合神經網路示意圖進行分析:

#由輸入層到隱藏層:

#由隱藏層到輸出層:

兩個公式來總結,可以得到:

Ij為目前層單元值,Oi為上一層的單元值,wij為兩層之間,連接兩個單元值的權重值,sitaj為每一層的偏向值。我們要對每一層的輸出進行非線性的轉換,示意圖如下:

當前層輸出為Ij,f為非線性轉化函數,又稱為激活函數,定義如下:

即每一層的輸出為:

這樣就可以透過輸入值正向得到每一層的輸出值。
2、根據誤差反向傳送對於輸出層:其中Tk是真實值,Ok是預測值

對於隱藏層:

權重更新:其中l為學習率

#偏向更新:

3、終止條件
偏重的更新低於某個閾值;
預測的錯誤率低於某個閾值;
達到預設一定的循環次數;
#4、非線性轉換函數
上述的非線性轉換函數f,一般情況下可以用兩種函數:
(1)tanh(x)函數:
tanh(x)=sinh(x)/cosh(x)
sinh(x)=(exp(x)-exp(-x))/2
cosh(x)=(exp( x)+exp(-x))/2
(2)邏輯函數,本文上面用的就是邏輯函數
五、BP神經網路的python實現
需要先導入numpy模組
import numpy as np
定義非線性轉換函數,由於還需要用到給函數的導數形式,因此一起定義
def tanh(x): return np.tanh(x) def tanh_deriv(x): return 1.0 - np.tanh(x)*np.tanh(x) def logistic(x): return 1/(1 + np.exp(-x)) def logistic_derivative(x): return logistic(x)*(1-logistic(x))
設計BP神經網路的形式(幾層,每層多少單元個數),用到了物件導向,主要是選擇哪種非線性函數,以及初始化權重。 layers是一個list,裡麵包含每一層的單元數。
class NeuralNetwork:
def __init__(self, layers, activation='tanh'):
"""
:param layers: A list containing the number of units in each layer.
Should be at least two values
:param activation: The activation function to be used. Can be
"logistic" or "tanh"
"""
if activation == 'logistic':
self.activation = logistic
self.activation_deriv = logistic_derivative
elif activation == 'tanh':
self.activation = tanh
self.activation_deriv = tanh_deriv
self.weights = []
for i in range(1, len(layers) - 1):
self.weights.append((2*np.random.random((layers[i - 1] + 1, layers[i] + 1))-1)*0.25)
self.weights.append((2*np.random.random((layers[i] + 1, layers[i + 1]))-1)*0.25)實作演算法
#
def fit(self, X, y, learning_rate=0.2, epochs=10000):
X = np.atleast_2d(X)
temp = np.ones([X.shape[0], X.shape[1]+1])
temp[:, 0:-1] = X
X = temp
y = np.array(y)
for k in range(epochs):
i = np.random.randint(X.shape[0])
a = [X[i]]
for l in range(len(self.weights)):
a.append(self.activation(np.dot(a[l], self.weights[l])))
error = y[i] - a[-1]
deltas = [error * self.activation_deriv(a[-1])]
for l in range(len(a) - 2, 0, -1):
deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))
deltas.reverse()
for i in range(len(self.weights)):
layer = np.atleast_2d(a[i])
delta = np.atleast_2d(deltas[i])
self.weights[i] += learning_rate * layer.T.dot(delta)實作預測
def predict(self, x):
x = np.array(x)
temp = np.ones(x.shape[0]+1)
temp[0:-1] = x
a = temp
for l in range(0, len(self.weights)):
a = self.activation(np.dot(a, self.weights[l]))
return afrom BP import NeuralNetwork import numpy as np nn = NeuralNetwork([2,2,1], 'tanh') x = np.array([[0,0], [0,1], [1,0], [1,1]]) y = np.array([1,0,0,1]) nn.fit(x,y,0.1,10000) for i in [[0,0], [0,1], [1,0], [1,1]]: print(i, nn.predict(i))
([0, 0], array([ 0.99738862])) ([0, 1], array([ 0.00091329])) ([1, 0], array([ 0.00086846])) ([1, 1], array([ 0.99751259]))
以上是詳解神經網路理論基礎及Python實作方法的詳細內容。更多資訊請關注PHP中文網其他相關文章!




