Javascript中數位儲存使用的是IEEE754 64位元雙精確度浮點數
在電腦中儲存為64位元
1 11 52
#1: 符號位元0正數1負數
11: 指數位用來決定範圍
52: 尾數位用來決定精確度
轉成十進位表示法為
num = (-1)^s * (1.f) * 2^E E = e - 1023 s:符号位 e:指数位 f:尾数位 1023偏正值 使得指数位真实取值为[-1023, 1024] 而非 [0, 2047] 目的是为了方便比较大小 实际指数值 = 阶码 - 偏正值 阶码 = 指数的移码 - 1 移码与补码符号为互为取反 举例: 如果指数位实际值为-1 原码:100 0000 0001 反码:111 1111 1110 补码:111 1111 1111 移码:011 1111 1111 阶码:011 1111 1110 = 1022 也可以通过 阶码 = 指数 + 偏正值 = -1 + 1023 = 1022 = 011 1111 1110来计算得到
指數位全0和全1有特殊意義,後面會講到,用來表示+-0 和+-∞
特殊值
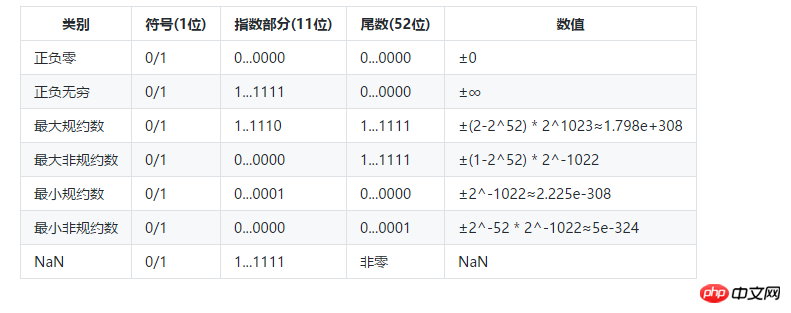
##機器精確度del = 2^-52
#首先我們計算下0.1的二進位
0.1 * 2 = 0
0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1
0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1
0.2 * 2 = 0
....
所以0.1的二進位為0.0001100110011001100 ...循環,
可以轉換為2^-4 * 1.100110011001100...
由於保留位數共52位,不包括最左邊整數位1,
所以最終在計算機中存儲的數值是:2^-4 * 1.100 11001100 11001100 11001100 11001100 11001100 11001100 1
0.2# 2 = 0. #0.6 * 2 = 1
0.2 * 2 = 0
0.4 * 2 = 0
0.8 * 2 = 1
0.6 * 2 = 1
...
所以0.2的二進位為0.001100110011001100...循環,
可以轉換為2^-3 * 1.100110011001100...
最容易最終在計算機中儲存的數值是:2^-3 * 1.100 1101010101010101010101 001100 11001100 1
兩者相加
0.0001100 11001100 11001100 11001100 11001100 11001100 11001100 1
+
0.00110101010101010101010101010101010101 00 11001100 11001100 1
= 0.0 10011001 10011001 10011001 10011001 10011001 10011001 10011001 10011001 10011001 1001001##00000
以上是解析js中0.1 + 0.2 != 0.3的詳細內容。更多資訊請關注PHP中文網其他相關文章!




