本文主要和大家介紹了使用css實現任意大小、任意方向和任意角度的箭頭示例的相關資料,小編覺得挺不錯的,現在分享給大家,也給大家做個參考,希望能幫助到大家。
網頁開發中,常會使用到下拉箭頭


#這樣的箭頭。 一般用css來實作:
{
display: inline-block;
margin: 72px;
border-top: 24px solid;
border-right: 24px solid;
width: 120px;
height: 120px;
transform: rotate(45deg);
}任意角度的箭頭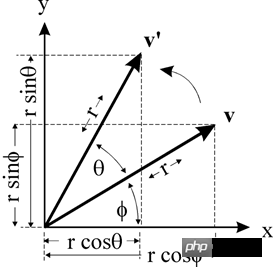
這裡有個問題: 假如需要一個角度為120度的箭頭呢? 由於border-top, border-right一直是90度, 所以光是旋轉不行。 我們可以先把p 旋轉45度, 讓它變成 菱形 然後再伸縮,達到任意的角度, 這樣就可以得到一個 任意角度的箭頭。由於用到了旋轉和伸縮兩種變換,所以需要使用
transform: matrix(a,b,c,d,e,f)這個變換矩陣。 這裡的6個變數組成了一個3介的變換矩陣
任意點p(x,y)的平移, 旋轉, 伸縮變換以及他們的各種組合都可以透過這個變換矩陣做到:註:這裡用齊次座標來表示一個點。 簡單說就是p(x, y) 表示為p'(x', y', 1)
平移矩陣
v(x, y) 沿著x軸平移tx, 沿著y軸平移ty。 則有:
##所以平移矩陣:x' = x + tx
y' = y + ty
旋轉矩陣
v(x, y) 點繞原點旋轉θ到v'(x', y')
則有:
x = r * cos(ϕ )
y = r * sin(ϕ )x' = r * cos(θ + ϕ) = r * cos(θ ) * cos(ϕ) - r * sin(θ) * sin(ϕ ) // 餘弦公式y' = r * sin(θ + ϕ) = r * sin(θ) * cos(ϕ) + r * cos(θ) * sin(ϕ ) // 正弦公式
所以:x' = x * cos(θ) - y * sin(θ)
y' = x * sin(θ) + y * cos(θ)所以旋轉矩陣:
伸縮矩陣
假設x軸,y軸的伸縮率分別是kx, ky。 則有:
x' = x * kxy' = y * ky
所以:複合變換
如果是對p(x, y)先平移(變換矩陣A), 然後旋轉(變換矩陣B), 然後伸縮(變換矩陣C)呢?
##p' =C(B(Ap)) ==> p' = (CBA)p //矩陣乘法結合率現在任意角度o的箭頭就很簡單了:
#先把p旋轉45度成為菱形, 轉換為M1
伸縮x軸, y軸:x' = size * cos(o/2) = x * √2 * cos(o/2)
y' = size * sin(o/2) = y * √2 * sin(o/2)

M3
那麼由於p' =C(B(Ap)) ==> p' = (CBA)p , 我們就可以先計算出M3
, 我們就可以先計算出M3
M1,然後對p進行對應的變換,就可以得到任意角度, 任意方向的箭頭了。 p的width和height就是箭頭的邊長, 透過調整可以取得任意邊長的箭頭。
 React元件
React元件
為了方便使用, 這個箭頭被封裝為了一個 React元件。
範例| #模擬select | |||
|---|---|---|---|
| select | |||
| 發散箭頭 | |||
| #name | |||
| default | description |
安装使用
npm install rc-arrow --save
import Arrow from 'rc-arrow'
class Hw extends Component {
render() {
return (
<Arrow size="20px" color="red"/>
)
}
}相关推荐:
以上是css實現任意大小、方向和角度的箭頭代碼的詳細內容。更多資訊請關注PHP中文網其他相關文章!




