交換排序:交換排序的基本思想是,比較兩個記錄鍵值的大小,如果這兩個記錄鍵值的大小出現逆序,則交換這兩個記錄,這樣將鍵值較小的記錄向序列前部移動,鍵值較大的記錄向序列後部移動。
一、冒泡排序
#介紹:
##氣泡排序(Bubble Sort,台灣譯為:泡沫排序或氣泡排序)是一種簡單的排序演算法。它重複地走訪過要排序的數列,一次比較兩個元素,如果他們的順序錯誤就把他們交換過來。走訪數列的工作是重複地進行直到沒有再需要交換,也就是說該數列已經排序完成。這個演算法的名字由來是因為越小的元素會經由交換慢慢「浮」到數列的頂端。
步驟:
#比較相鄰的元素。如果第一個比第二個大,就交換他們兩個。
對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對。在這一點,最後的元素應該會是最大的數字。
針對所有的元素重複以上的步驟,除了最後一個。
持續每次對越來越少的元素重複上面的步驟,直到沒有任何一對數字需要比較。
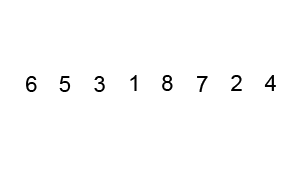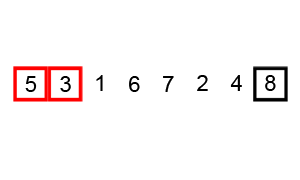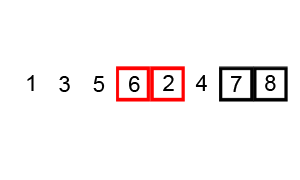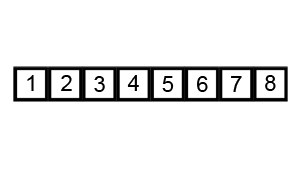
#冒泡排序理解起來是最簡單,但是時間複雜度( O(n^2))也是最大的之一,實作程式碼如下:#
<br/>
$arr=#array(1,43,54,62,21,66 ,32,78,36,76,39);
function## getpao($arr)
#{
$len=count(
); //設定空數組 用來接收冒出來的泡 //此層循環控制 需要冒泡的輪數###
for($i
=1;######$i######<######$ len######;######$i######++) ##################### { ### //此層循環用來控制每回合 冒出一個數 需要比較的次數###### ##########for($k=0;##$k<$len-$i;$k# ++)
# {
## ($arr[$k]>$arr# [$k+1])
H之一# $tmp=
##$arr# # +1]; ## $arr##[$k+1] = $arr[
$k######]; ##########$arr[##$k]=$tmp;
}
#
$ arr;
介紹:
快速排序是由東尼·霍爾
所發展的一種排序演算法。在平均狀況下,排序n 個項目要進行Ο(n log n)次比較。在最壞狀況下則需要Ο(n2)次比較,但這種狀況並不常見。事實上,快速排序通常明顯比其他Ο(n log n) 演算法更快,因為它的內部循環(inner loop)可以大部分的架構上很有效率地被實現出來,且在大部分真實世界的數據,可以決定設計的選擇,減少所需時間的二次方項之可能性。
步驟:# 從數列中挑出一個元素,稱為「基準」(pivot), 重新排序序列,所有元素比基準值小的擺放在基準前面,所有元素比基準值大的擺在基準的後面(相同的數可以到任一邊)。在這個分區退出之後,該基準就處於數列的中間位置。這個稱為分區(partition)操作。 遞歸地(recursive)將小於基準值元素的子數列和大於基準值元素的子數列排序。 #快排也是一個高效率的排序演算法,它的時間複雜度也是O( nlogn)。程式碼如下: function# quick_sort($arr) { //先判斷是否需要繼續進行 $length = count #return $arr##; # } # = $arr[0]; #//遍歷 除了尺外的所有元素,依照大小關係放入兩個數組內 ## # #//初始化兩個陣列 $left_array = array();//小於尺的 for($i=1; $i<$length; #$i++) { # if($base_num## > $arr# > $arr[$i ///放入陣列 #$$arrleft_array[] #[$i]; } else# { #//放入右側# $right_array[] = $arr#$i]; # } # # //再分別對 左邊 和 右邊的陣列進行相同的排序處理方式 # //遞迴呼叫這個函數,並記錄結果 # $left_array = quick_sort($left_array); $right_array = quick_sort( return array_merge(#$left_array , array($base_num), ##$right_array); #} #選擇排序 <br/> ######## 選擇排序包括兩種,分別是直接選擇排序和堆疊排序,選擇排序的基本思想是每次在n-i+ 1(i=1,2,3,...,n-1)記錄中選取鍵值最小的記錄作為有序序列的第i個記錄############### #三、選擇排序### #########介紹:#############選擇排序(Selection sort)是一種簡單直覺的######排序演算法######.它的工作原理如下。首先在未排序序列中找出最小元素,存放到排序序列的起始位置,然後,再從剩餘未排序元素中繼續尋找最小元素,然後放到排序序列末端。以此類推,直到所有元素都排序完畢。 #####################選擇排序理解起來也比較簡單,時間複雜度也是O(n^2),實作程式碼如下:### function# select_sort($arr ##//實作想法 雙重循環完成,外層控制輪數,目前的最小值。內層 控制的比較次數 //$i 目前最小值的位置, 則需要參與比較的元素 # for(#$i =0, $len ($arr) ; $len-1; ##$i++ ) { //先假設最小的值的位置 for($j##=#$i#$i# #+1; $j<$len ++) { o##H#STST夥計 M板雜劑目前。 ## if( ##( $$ p //已決定了目前的最小值的位置,並儲存到$p。 //若發現 最小值的位置與目前假設的位置$i不同,則位置互換來 # if#(#$p != $i) { ## = $arr[$p]; $arr[ $arr $arr#############. [######$i######]; ##################### ###$arr#######[ ######$i######] = ######$tmp######; ########################### ## } ################### } ################################################################################################################################################ //傳回最終結果 # return ; } <br/> ##四、堆排序 介紹: 堆 堆排序是一种高效的排序算法,它的时间复杂度是O(nlogn)。原理是:先把数组转为一个最大堆,然后把第一个元素跟第i元素交换,然后把剩下的i-1个元素转为最大堆,然后再把第一个元素与第i-1个元素交换,以此类推。实现代码如下: <br/> <br/> 插入排序 五、插入排序 介绍: 插入排序(Insertion Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。 步骤: 从第一个元素开始,该元素可以认为已经被排序 取出下一个元素,在已经排序的元素序列中从后向前扫描 如果该元素(已排序)大于新元素,将该元素移到下一位置 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置 将新元素插入到该位置中 重复步骤2 [php] view plain copy <br/> ##function insert_sort( ########################### ###### ###//區分 哪一部分是已排序好的###### ##################### ###/ /哪個部分是沒有排序的###### ##################### ###//找出其中一個需要排序的元素#### ## ##################### ###//這個元素 就是從第二個元素開始,到最後一個元素都是這個需要排序的元素# ##### ##################### ###//利用迴圈就可以標誌出來##### ############## ######## ############## ###//i循環控制 每次需要插入的元素,一旦需要插入的元素控制了,###### ###### ############### ###//間接將陣列分成了2部分,下標小於目前的(左邊的),是排序好的序列####### ########## for($i=1, $len=count($arr); $i< ;$len; $i#++) { $arr# = ##1 [$i]; #///內層循環控制比較 並 插入 //$arr[$i];//需要插入的元素; $arr[$j];//需要比較的元素 # if($tmp## <##($tmp## < #$arr[$j]) { ####################### # ###//發現插入的元素較小,交換位置##### ##################### ###//將後邊的元素元素與前面的元素互換###### ##################### ###$arr #$j######+1] = ######$arr#######[######$j#####]; ################################################################# ############# ###//將前一個的數字設定為 目前需要交換的數字#######o# ###### ###$arr######[######$j######] = ############$j######] =##################'> ####### } else { //如果碰到不需要移动的元素 //由于是已经排序好是数组,则前面的就不需要再次比较了。 break; } } } //将这个元素 插入到已经排序好的序列内。 //返回 return $arr; } 六、希尔排序 介绍: 希尔排序,也称递减增量排序算法,是插入排序的一种高速而稳定的改进版本。 希尔排序是基于插入排序的以下两点性质而提出改进方法的: 1、插入排序在对几乎已经排好序的数据操作时, 效率高, 即可以达到线性排序的效率 2、但插入排序一般来说是低效的, 因为插入排序每次只能将数据移动一位> 排序效果: <br/> 七、归并排序 介绍: 归并排序(Merge sort,台湾译作:合并排序)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(pide and Conquer)的一个非常典型的应用 步骤: 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列 设定两个指针,最初位置分别为两个已经排序序列的起始位置 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置 重复步骤3直到某一指针达到序列尾 将另一序列剩下的所有元素直接复制到合并序列尾 排序效果: 我们先来看看主函数部分: 在总函数中,我们只调用了一个 MSort() 函数,因为我们要使用递归调用,所以将 MSort() 封装起来。 下面我们来看看 MSort() 函数: 上面的 MSort() 函数实现将数组分半再分半(直到子序列长度为1),然后将子序列合并起来。 现在是我们的归并操作函数 Merge() : 到了这里,我们的归并算法就完了。我们调用试试:
 <br/>
<br/><br/>
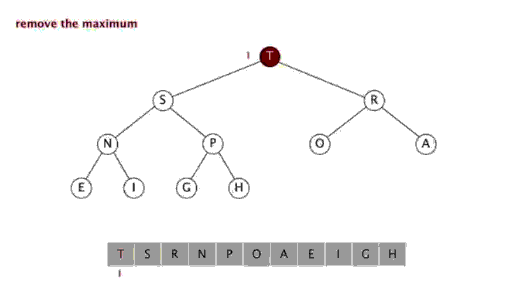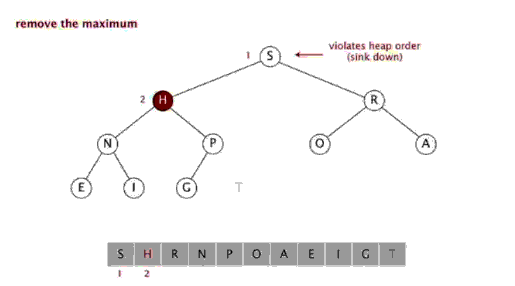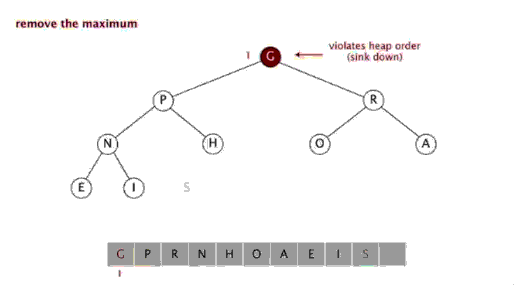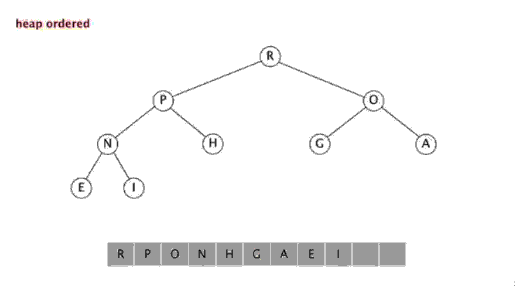
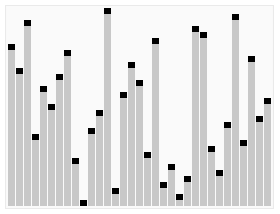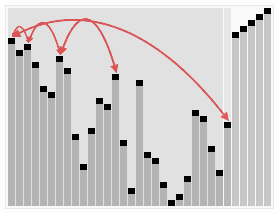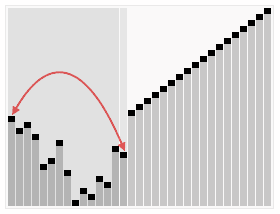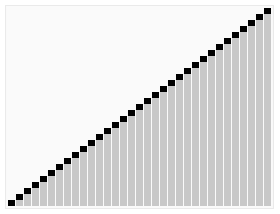 <br/>
<br/>function heapSort($arr) {
$len = count($arr); // 先建立最大堆
for ($i = floor(($len - 1) / 2); $i >= 0; $i--) { $s = $i; $childIndex = $s * 2 + 1; while ($childIndex < $len) { // 在父、左子、右子中 ,找到最大的
if ($childIndex + 1 < $len && $arr[$childIndex] < $arr[$childIndex + 1]) $childIndex++; if ($arr[$s] < $arr[$childIndex]) { $t = $arr[$s]; $arr[$s] = $arr[$childIndex]; $arr[$childIndex] = $t; $s = $childIndex; $childIndex = $childIndex * 2 + 1;
} else { break;
}
}
} // 从最后一个元素开始调整
for ($i = $len - 1; $i > 0; $i--) { $t = $arr[$i]; $arr[$i] = $arr[0]; $arr[0] = $t; // 调整第一个元素
$s = 0; $childIndex = 1; while ($childIndex < $i) { // 在父、左子、右子中 ,找到最大的
if ($childIndex + 1 < $i && $arr[$childIndex] < $arr[$childIndex + 1]) $childIndex++; if ($arr[$s] < $arr[$childIndex]) { $t = $arr[$s]; $arr[$s] = $arr[$childIndex]; $arr[$childIndex] = $t; $s = $childIndex; $childIndex = $childIndex * 2 + 1;
} else { break;
}
}
} return $arr;
}$arr = [3,1,13,5,7,11,2,4,14,9,15,6,12,10,8];
print_r(bubbleSort($arr)); <br/>感觉插入排序跟冒泡排序有点相似,时间复杂度也是O(n^2),实现代码如下:
<br/>感觉插入排序跟冒泡排序有点相似,时间复杂度也是O(n^2),实现代码如下:<br/>
 <br/>希尔排序其实可以理解是插入排序的一个优化版,它的效率跟增量有关,增量要取多少,根据不同的数组是不同的,所以希尔排序是一个不稳定的排序算法,它的时间复杂度为O(nlogn)到O(n^2)之间,实现代码如下:
<br/>希尔排序其实可以理解是插入排序的一个优化版,它的效率跟增量有关,增量要取多少,根据不同的数组是不同的,所以希尔排序是一个不稳定的排序算法,它的时间复杂度为O(nlogn)到O(n^2)之间,实现代码如下:function shellSort($arr) {
$len = count($arr); $stepSize = floor($len / 2); while ($stepSize >= 1) { for ($i = $stepSize; $i < $len; $i++) { if ($arr[$i] < $arr[$i - $stepSize]) { $t = $arr[$i]; $j = $i - $stepSize; while ($j >= 0 && $t < $arr[$j]) { $arr[$j + $stepSize] = $arr[$j]; $j -= $stepSize;
} $arr[$j + $stepSize] = $t;
}
} // 缩小步长,再进行插入排序
$stepSize = floor($stepSize / 2);
} return $arr;
}$arr = [3,1,13,5,7,11,2,4,14,9,15,6,12,10,8];
print_r(bubbleSort($arr)); <br/>归并排序的时间复杂度也是O(nlogn)。原理是:对于两个排序好的数组,分别遍历这两个数组,获取较小的元素插入新的数组中,那么,这么新的数组也会是排序好的。代码如下:
<br/>归并排序的时间复杂度也是O(nlogn)。原理是:对于两个排序好的数组,分别遍历这两个数组,获取较小的元素插入新的数组中,那么,这么新的数组也会是排序好的。代码如下://交换函数function swap(array &$arr,$a,$b){
$temp = $arr[$a]; $arr[$a] = $arr[$b]; $arr[$b] = $temp;
}//归并算法总函数function MergeSort(array &$arr){
$start = 0; $end = count($arr) - 1;
MSort($arr,$start,$end);
}function MSort(array &$arr,$start,$end){ //当子序列长度为1时,$start == $end,不用再分组 if($start < $end){ $mid = floor(($start + $end) / 2); //将 $arr 平分为 $arr[$start - $mid] 和 $arr[$mid+1 - $end] MSort($arr,$start,$mid); //将 $arr[$start - $mid] 归并为有序的$arr[$start - $mid] MSort($arr,$mid + 1,$end); //将 $arr[$mid+1 - $end] 归并为有序的 $arr[$mid+1 - $end] Merge($arr,$start,$mid,$end); //将$arr[$start - $mid]部分和$arr[$mid+1 - $end]部分合并起来成为有序的$arr[$start - $end]
}
}//归并操作function Merge(array &$arr,$start,$mid,$end){
$i = $start; $j=$mid + 1; $k = $start; $temparr = array(); while($i!=$mid+1 && $j!=$end+1)
{ if($arr[$i] >= $arr[$j]){ $temparr[$k++] = $arr[$j++];
} else{ $temparr[$k++] = $arr[$i++];
}
} //将第一个子序列的剩余部分添加到已经排好序的 $temparr 数组中
while($i != $mid+1){ $temparr[$k++] = $arr[$i++];
} //将第二个子序列的剩余部分添加到已经排好序的 $temparr 数组中
while($j != $end+1){ $temparr[$k++] = $arr[$j++];
} for($i=$start; $i<=$end; $i++){ $arr[$i] = $temparr[$i];
}
}$arr = array(9,1,5,8,3,7,4,6,2);
MergeSort($arr);
var_dump($arr);
相关推荐:
以上是php實作幾種常見的排序演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章!




