用TensorFlow實作lasso迴歸和嶺迴歸演算法的範例
這篇文章主要介紹了關於用TensorFlow實現lasso回歸和嶺回歸演算法的範例,有著一定的參考價值,現在分享給大家,有需要的朋友可以參考一下
也有些正規方法可以限制迴歸演算法輸出結果中係數的影響,其中最常用的兩種正規方法是lasso迴歸和嶺迴歸。
lasso迴歸和嶺迴歸演算法跟常規線性迴歸演算法極為相似,有一點不同的是,在公式中增加正規項來限制斜率(或淨斜率)。這樣做的主要原因是限制特徵對因變數的影響,透過增加一個依賴斜率A的損失函數來實現。
對於lasso迴歸演算法,在損失函數上增加一項:斜率A的某個給定倍數。我們使用TensorFlow的邏輯操作,但沒有這些操作相關的梯度,而是使用階躍函數的連續估計,也稱為連續階躍函數,其會在截止點跳躍擴大。一會兒就可以看到如何使用lasso迴歸演算法。
對於嶺迴歸演算法,增加一個L2範數,即斜率係數的L2正則。
# LASSO and Ridge Regression
# lasso回归和岭回归
#
# This function shows how to use TensorFlow to solve LASSO or
# Ridge regression for
# y = Ax + b
#
# We will use the iris data, specifically:
# y = Sepal Length
# x = Petal Width
# import required libraries
import matplotlib.pyplot as plt
import sys
import numpy as np
import tensorflow as tf
from sklearn import datasets
from tensorflow.python.framework import ops
# Specify 'Ridge' or 'LASSO'
regression_type = 'LASSO'
# clear out old graph
ops.reset_default_graph()
# Create graph
sess = tf.Session()
###
# Load iris data
###
# iris.data = [(Sepal Length, Sepal Width, Petal Length, Petal Width)]
iris = datasets.load_iris()
x_vals = np.array([x[3] for x in iris.data])
y_vals = np.array([y[0] for y in iris.data])
###
# Model Parameters
###
# Declare batch size
batch_size = 50
# Initialize placeholders
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
# make results reproducible
seed = 13
np.random.seed(seed)
tf.set_random_seed(seed)
# Create variables for linear regression
A = tf.Variable(tf.random_normal(shape=[1,1]))
b = tf.Variable(tf.random_normal(shape=[1,1]))
# Declare model operations
model_output = tf.add(tf.matmul(x_data, A), b)
###
# Loss Functions
###
# Select appropriate loss function based on regression type
if regression_type == 'LASSO':
# Declare Lasso loss function
# 增加损失函数,其为改良过的连续阶跃函数,lasso回归的截止点设为0.9。
# 这意味着限制斜率系数不超过0.9
# Lasso Loss = L2_Loss + heavyside_step,
# Where heavyside_step ~ 0 if A < constant, otherwise ~ 99
lasso_param = tf.constant(0.9)
heavyside_step = tf.truep(1., tf.add(1., tf.exp(tf.multiply(-50., tf.subtract(A, lasso_param)))))
regularization_param = tf.multiply(heavyside_step, 99.)
loss = tf.add(tf.reduce_mean(tf.square(y_target - model_output)), regularization_param)
elif regression_type == 'Ridge':
# Declare the Ridge loss function
# Ridge loss = L2_loss + L2 norm of slope
ridge_param = tf.constant(1.)
ridge_loss = tf.reduce_mean(tf.square(A))
loss = tf.expand_dims(tf.add(tf.reduce_mean(tf.square(y_target - model_output)), tf.multiply(ridge_param, ridge_loss)), 0)
else:
print('Invalid regression_type parameter value',file=sys.stderr)
###
# Optimizer
###
# Declare optimizer
my_opt = tf.train.GradientDescentOptimizer(0.001)
train_step = my_opt.minimize(loss)
###
# Run regression
###
# Initialize variables
init = tf.global_variables_initializer()
sess.run(init)
# Training loop
loss_vec = []
for i in range(1500):
rand_index = np.random.choice(len(x_vals), size=batch_size)
rand_x = np.transpose([x_vals[rand_index]])
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
loss_vec.append(temp_loss[0])
if (i+1)%300==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b)))
print('Loss = ' + str(temp_loss))
print('\n')
###
# Extract regression results
###
# Get the optimal coefficients
[slope] = sess.run(A)
[y_intercept] = sess.run(b)
# Get best fit line
best_fit = []
for i in x_vals:
best_fit.append(slope*i+y_intercept)
###
# Plot results
###
# Plot regression line against data points
plt.plot(x_vals, y_vals, 'o', label='Data Points')
plt.plot(x_vals, best_fit, 'r-', label='Best fit line', linewidth=3)
plt.legend(loc='upper left')
plt.title('Sepal Length vs Pedal Width')
plt.xlabel('Pedal Width')
plt.ylabel('Sepal Length')
plt.show()
# Plot loss over time
plt.plot(loss_vec, 'k-')
plt.title(regression_type + ' Loss per Generation')
plt.xlabel('Generation')
plt.ylabel('Loss')
plt.show()輸出結果:
Step #300 A = [[ 0.77170753]] b = [[ 1.82499862]]
Loss = [[ 10.26473045]]
Step #600 A = [[ 0.75908542]] b = [[ 3.2220633]]
Loss = [[ 3.06292033]]##Step #007485. ] b = [[ 3.9975822]]
Loss = [[ 1.23220456]]
Step #1200 A = [[ 0.73752165]] b = [[ 4.42974091]]##Loss5 = [ ] b = [[ 4.42974091]]##Loss5 = [ 0.57]#7057]#。 #Step #1500 A = [[ 0.72942668]] b = [[ 4.67253113]]
Loss = [[ 0.40874988]]
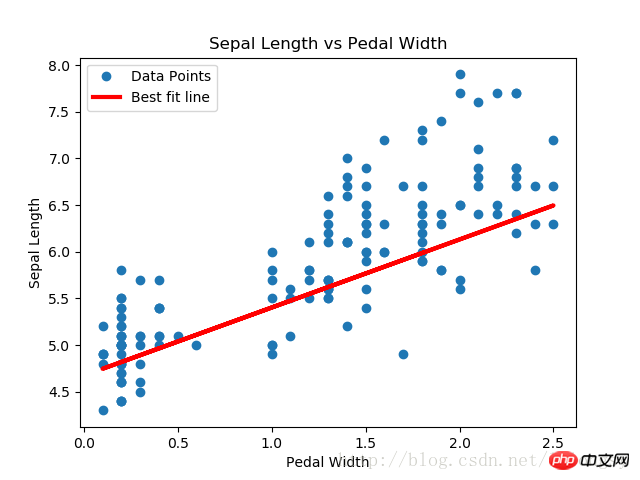
透過在標準線性迴歸估計的基礎上,增加一個連續的階躍函數,實現lasso迴歸演算法。由於階躍函數的坡度,我們需要注意步長,因為太大的步長會導致最終不收斂。 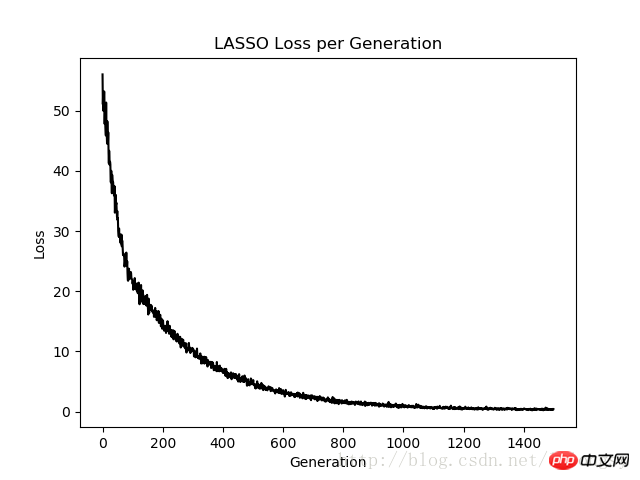
用TensorFlow實作戴明迴歸演算法的範例
以上是用TensorFlow實作lasso迴歸和嶺迴歸演算法的範例的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 迎接國服回歸,暴雪白送魔獸世界第2珍奇坐騎,掉率低於萬分之一!
Apr 15, 2024 pm 02:20 PM
迎接國服回歸,暴雪白送魔獸世界第2珍奇坐騎,掉率低於萬分之一!
Apr 15, 2024 pm 02:20 PM
在魔獸世界10.27的熊貓人活動中,暴雪將白送神聖瑪瑙雲端翔龍!這條坐騎當年的掉率低於萬分之一!如果不是為了迎接國服回歸,小探相信暴雪絕對不會這麼大方。
 conda怎麼安裝tensorflow
Dec 05, 2023 am 11:26 AM
conda怎麼安裝tensorflow
Dec 05, 2023 am 11:26 AM
安裝步驟:1、下載和安裝Miniconda,依照作業系統選擇適合的Miniconda版本,並依照官方指南進行安裝;2、使用「conda create -n tensorflow_env python=3.7」指令建立一個新的Conda環境;3、啟動Conda環境;4、使用「conda install tensorflow」指令安裝最新版的TensorFlow;5、驗證安裝即可。
 十個AI演算法常用函式庫Java版
Jun 13, 2023 pm 04:33 PM
十個AI演算法常用函式庫Java版
Jun 13, 2023 pm 04:33 PM
今年ChatGPT火了半年多,熱度絲毫沒有降下來。深度學習和NLP也重新回到了大家的視線中。公司裡有一些小夥伴都在問我,身為Java開發人員,如何入門人工智慧,是時候拿出壓箱底的私藏的學習AI的Java庫來介紹給大家。這些函式庫和框架為機器學習、深度學習、自然語言處理等提供了廣泛的工具和演算法。根據AI專案的具體需求,可以選擇最合適的函式庫或框架,並開始嘗試使用不同的演算法來建立AI解決方案。 1.Deeplearning4j它是一個用於Java和Scala的開源分散式深度學習函式庫。 Deeplearning
 使用TensorFlow和Keras建立貓狗圖片深度學習分類器
May 16, 2023 am 09:34 AM
使用TensorFlow和Keras建立貓狗圖片深度學習分類器
May 16, 2023 am 09:34 AM
在本文中,我們將使用TensorFlow和Keras建立一個影像分類器,可以區分貓和狗的影像。為了做到這一點,我們將使用TensorFlow資料集中的cats_vs_dogs資料集。該資料集由25000張打過標籤的貓狗的圖像組成,其中80%的圖像用於訓練,10%用於驗證,10%用於測試。載入資料我們從使用TensorFlowDatasets載入資料集開始。將資料集拆分為訓練集、驗證集和測試集,分別佔資料的80%、10%和10%,並定義一個函數來顯示資料集中的一些樣本影像。 importtenso
 網易平台開啟回歸活動,暴雪新CG增加國服版本,重開只剩下最後一步
Mar 31, 2024 am 10:01 AM
網易平台開啟回歸活動,暴雪新CG增加國服版本,重開只剩下最後一步
Mar 31, 2024 am 10:01 AM
國服回歸的消息已經逐漸從舅舅黨爆料過渡到官方明里暗裡的小動作了,下面胖哥跟大家分享一下最新的消息。第一個消息:KK對戰平台開啟回歸活動最近一段時間一直有玩家在KK對戰平台的評論區詢問國服回歸的進程,而該平台的小編則表示自己很想說,但是領導不讓說,之後會給玩家「來波大的」。目前KK對戰平台已經開啟了國服回歸活動,贈送玩家們魔獸世界國服月卡,並且針對國服回歸進行了暗示:「春天來了好事將近,你懂得」。很多玩家會疑惑,為什麼國服的事情要問KK對戰平台?其實原因就是KK對戰平臺本身就是網易的。國服關閉前
 魔獸世界國服重開之際,4大版選擇指南,最後1個更適合休閒玩家
Apr 13, 2024 am 09:16 AM
魔獸世界國服重開之際,4大版選擇指南,最後1個更適合休閒玩家
Apr 13, 2024 am 09:16 AM
魔獸世界目前存在4個版本,國服關閉這一年多,估計很多玩家都不知道各版本發展到哪一步了,下面胖哥就給大家梳理一下各版本的現狀。 1,正式服務10.0版末期國服關閉前是10.0版本才剛開始,目前已經處於10.26版本了,後面還有一個10.27版本,巨龍時代資料片就結束了。雖然10.0版在外服的評價不錯,並且為暴雪挽回了一些人氣,但是10.0版本的遊戲內核是沒有任何變化的,依然是大祕境和團本為主,PVP玩家人數少之又少。隨著正式服版本的不斷更新,玩家們的遊戲傾向也從PVE和PVP變成了收集,每月商棧上
 pip安裝tensorflow教程
Dec 07, 2023 pm 03:50 PM
pip安裝tensorflow教程
Dec 07, 2023 pm 03:50 PM
安裝步驟:1、確保已經安裝了Python和pip;2、開啟命令提示字元或終端機窗口,輸入「pip install tensorflow」指令安裝TensorFlow;3、若想安裝CPU版本的TensorFlow,可以使用「pip install tensorflow- cpu」指令;4、安裝完成後,即可在Python中使用TensorFlow。
 暴雪已備好國服大禮準備魔獸開服,回歸玩家突破200萬!考迪克被暴打!
Apr 12, 2024 pm 03:37 PM
暴雪已備好國服大禮準備魔獸開服,回歸玩家突破200萬!考迪克被暴打!
Apr 12, 2024 pm 03:37 PM
今天是暴雪國服停服的第445天。歡迎繼續關注當前風靡全球很快又會有國服的大型網路交友聊天室遊戲《魔獸世界》的最新消息。國服人氣炸裂,首日回歸玩家突破200萬4月11日晚,魔獸世界官方微博發布了一條重磅消息,僅僅4月10日官宣的那一天(也就是官宣之後的15小時之內),成功登入並且完成預約的暴雪國服玩家數量就達到了200萬!同時,在重鑄血吼活動留言的玩家數量也達到了95萬多,逼近100萬。不僅如此,網易還成功幫助玩家修復的帳號數量達到9.2萬個,成功找回的帳號數量則達到了14.7萬。這是一個非常誇張






