如何在canvas裡面基於隨機點繪製一個多邊形
這篇文章主要介紹了canvas裡面如何基於隨機點繪製一個多邊形的方法的相關資料,內容挺不錯的,現在分享給大家,也給大家做個參考。
起因
今天在學習《HTML5 Javascript動畫基礎》這本書的時候,在第八章的第三節講到如何用三個彈簧連接三個點來做伸展運動。
做完例子之後,就想到如果是四個點,五個點,怎麼樣。
就改寫了一下程式碼,把點的數目變數化。最終的效果是能實現各點最終的伸展運動到平衡,可是點之間的連線不是很好看,有些是交叉的。
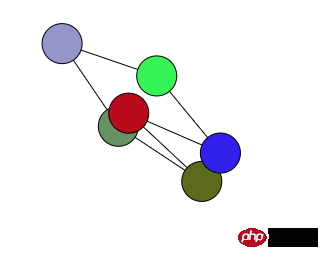
於是就想著能不能優化這一塊。
旋轉連線
前面範例裡面的點,都是隨機位置,所以連線不可控。所以想先從這塊著手。
先以某一點為參考點,得到其他點相對於這個點的角度。
然後按照角度從小到大的去連接這些點,這樣就能畫出一個正常的多邊形了。
大致實作程式碼如下:
let balls = [];
let ballNum = 6;
let firstBall = null;
while(ballNum--) {
let ball = new Ball(20, parseColor(Math.random() * 0xffffff))
ball.x = Math.random() * width;
ball.y = Math.random() * height;
balls.push(ball)
if (!firstBall) {
firstBall = ball
ball.angle = 0
} else {
const dx = ball.x - firstBall.x,
dy = ball.y - firstBall.y;
ball.angle = Math.atan2(dy, dx);
}
}
// 尝试让球连线是一个正多边形
balls = balls.sort((ballA, ballB) => {
return ballA.angle - ballB.angle
})#這樣在最後繪製連線的時候,遍歷陣列就能依照角度從小到大來繪製了。
效果如下:

這樣是能極大的減少交叉線的情況,可還是無法完全避免。
接下來,想嘗試優化這個方案,例如angle用Math.abs來取正,或是每個點都找夾角最小的點來連線。可是結果都不行,無法避免交叉線。
基於中心點旋轉
後面又想到一個思路,如果能確定多邊形的中心點,那麼分別計算所有點相對於中心點的夾角,就能以順時針或逆時針連接這些點。
可是在網路上找了半天,所有點演算法裡面,都是要求有一系列依照某個時針順序排列的點。
可是如果我有這些點,就已經能畫出多邊形了。只好放棄
X軸兩極點分割
#無奈之下只好找Google,然後就發現了知乎上的一個答案挺好的: 如何將平面上無序的一組點連成一個簡單多邊形?
具體演算法描述,大家看那個答案就好,我就不贅述了。
不過在連接上鍊和下鍊的時候,其實只要確保上鍊是X軸降序連接,下鍊是X軸升序連接即可(以逆時針方向繪製)。至於X軸相同的點,不管是優先Y軸大的還是小的都可以。
實現的時候,是嚴格按照答案裡面的演算法實現的。
在判斷一個點是屬於上鍊還是下鏈的時候,一開始想的是基於兩點決定直線的函數方程,再引入點的座標來計算。不過後面想到,所有的點都以最左邊的極點來計算斜角,然後根據角度大小來劃分,視覺上更好理解。
大致程式碼如下:
let balls = [];
let tempBalls = [];
let ballNum = 6;
let isDragingBall = false;
while(ballNum--) {
let ball = new Ball(10, parseColor(Math.random() * 0xffffff))
ball.x = Math.random() * width;
ball.y = Math.random() * height;
tempBalls.push(ball)
}
// 让点按X轴升序排序
tempBalls = tempBalls.sort((ballA, ballB) => {
return ballA.x - ballB.x
})
// 找X轴左右极点
let firstBall = tempBalls[0],
lastBall = tempBalls[tempBalls.length -1];
let smallXBalls = tempBalls.filter(ball => ball.x === firstBall.x),
bigXBalls = tempBalls.filter(ball => ball.x === lastBall.x)
// 处理左右极点有多个的情况
if (smallXBalls.length > 1) {
smallXBalls.sort((ballA, ballB) => {
return ballB.y - ballA.y
})
}
if (bigXBalls.length > 1) {
bigXBalls.sort((ballA, ballB) => {
return ballB.y - ballA.y
})
}
firstBall = smallXBalls[0]
lastBall = bigXBalls[0]
// 获得极点连线的角度
let splitLineAngle = Math.atan2(lastBall.y - firstBall.y, lastBall.x - firstBall.x);
let upperBalls = [],
lowerBalls = [];
// 所有其他点跟firstBall计算角度
// 大于splitLineAngle的都是下链
// 其他是上链
tempBalls.forEach(ball => {
if (ball === firstBall || ball === lastBall) {
return false
}
let angle = Math.atan2(ball.y - firstBall.y, ball.x - firstBall.x);
if (angle > splitLineAngle) {
lowerBalls.push(ball)
} else {
upperBalls.push(ball)
}
})
// 处理X轴相同情况的排序
lowerBalls = lowerBalls.sort((ballA, ballB) => {
if (ballA.x !== ballB.x) {
return ballA.x - ballB.x
}
return ballB.y - ballA.y
})
upperBalls = upperBalls.sort((ballA, ballB) => {
if (ballA.x !== ballB.x) {
return ballB.x - ballA.x
}
return ballB.y - ballB.x
})
// 逆时针连接所有的点
balls = [firstBall].concat(lowerBalls, [lastBall], upperBalls)
balls = balls.map((ball, i) => {
ball.text = i + 1;
return ball
})最終回傳的balls,就是以逆時針排序的多邊形的點了。
效果如下:
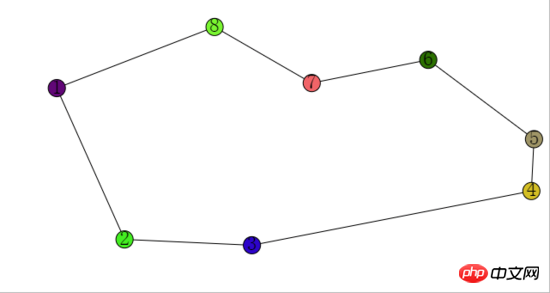
各球的內部狀態如下:

使用html5
canvas封裝一個echarts實作不了的餅圖
#
以上是如何在canvas裡面基於隨機點繪製一個多邊形的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 建築ppt可以直接畫平面圖嗎
Mar 20, 2024 am 08:43 AM
建築ppt可以直接畫平面圖嗎
Mar 20, 2024 am 08:43 AM
ppt在許多領域和工作中都被廣泛使用,教育類、建築類等等的使用更是普遍。提到建築ppt,肯定我們首先想到的是一些建築類圖紙的呈現,如果我們沒有使用專業圖面繪畫軟體,能不能直接繪製簡單的建築平面圖呢?其實,這裡,我們是可以完成操作的,下邊,我們就繪製一個比較簡單的平面圖,給大家一個思路,希望大家能夠在這個思路下完成更好的平面圖繪製。 1.首先,我們雙擊開啟桌面上ppt軟體,點選新建示範空白文件。 2.我們在功能表列找到插入→形狀→矩形。 3.繪製矩形完成,隨後,雙擊圖形,我們修改填滿顏色類型,這裡我們可以修
 七邊形數
Sep 24, 2023 am 10:33 AM
七邊形數
Sep 24, 2023 am 10:33 AM
Aheptagonalnumberisanumberwhichcanberepresentedasaheptagon.Aheptagonisapolygonwith7sides.Aheptagonalnumbercanberepresentedasacombinationofsuccessivelayersofheptagon(7-sidedpolygon).Heptagonalnumbercanbebetterexpexpmedwiththebelowgures.第一個七邊形數是第一個七邊形數。因此,
 學習canvas框架 詳解常用的canvas框架
Jan 17, 2024 am 11:03 AM
學習canvas框架 詳解常用的canvas框架
Jan 17, 2024 am 11:03 AM
探索Canvas框架:了解常用的Canvas框架有哪些,需要具體程式碼範例引言:Canvas是HTML5中提供的一個繪圖API,透過它我們可以實現豐富的圖形和動畫效果。為了提高繪圖的效率和便利性,許多開發者開發了不同的Canvas框架。本文將介紹一些常用的Canvas框架,並提供具體程式碼範例,以幫助讀者更深入地了解這些框架的使用方法。一、EaselJS框架Ea
 如何用Python繪製3D地理圖表
Sep 28, 2023 am 10:19 AM
如何用Python繪製3D地理圖表
Sep 28, 2023 am 10:19 AM
如何用Python繪製3D地理圖表概述:繪製3D地理圖表可以幫助我們更直觀地理解地理資料和空間分佈。 Python作為一種功能強大且易於使用的程式語言,提供了許多程式庫和工具,可用於繪製各種類型的地理圖表。在本文中,我們將學習如何使用Python程式語言和一些流行的函式庫,如Matplotlib和Basemap,來繪製3D地理圖表。環境準備:在開始之前,我們需要確保已
 html2canvas有哪些版本
Aug 22, 2023 pm 05:58 PM
html2canvas有哪些版本
Aug 22, 2023 pm 05:58 PM
html2canvas的版本有html2canvas v0.x、html2canvas v1.x等。詳細介紹:1、html2canvas v0.x,這是html2canvas的早期版本,目前最新的穩定版本是v0.5.0-alpha1。它是一個成熟的版本,已經被廣泛使用,並且在許多專案中得到了驗證;2、html2canvas v1.x,這是html2canvas的新版本。
 五分鐘學會用Python繪製樹狀圖和雷達圖
Sep 27, 2023 pm 12:48 PM
五分鐘學會用Python繪製樹狀圖和雷達圖
Sep 27, 2023 pm 12:48 PM
五分鐘學會用Python繪製樹狀圖和雷達圖在資料視覺化中,樹狀圖和雷達圖是兩種常用的圖表形式。樹狀圖用於展示層級結構,而雷達圖則用於比較多個維度的資料。本文將介紹如何使用Python繪製這兩種圖表,並提供具體的程式碼範例。一、繪製樹狀圖Python中有多個庫可以用來繪製樹狀圖,如matplotlib和graphviz。以下以使用matplotlib庫為例,演示
 uniapp實現如何使用canvas繪製圖表和動畫效果
Oct 18, 2023 am 10:42 AM
uniapp實現如何使用canvas繪製圖表和動畫效果
Oct 18, 2023 am 10:42 AM
uniapp實現如何使用canvas繪製圖表和動畫效果,需要具體程式碼範例一、引言隨著行動裝置的普及,越來越多的應用程式需要在行動裝置上展示各種圖表和動畫效果。而uniapp作為一款基於Vue.js的跨平台開發框架,提供了使用canvas繪製圖表和動畫效果的能力。本文將介紹uniapp如何使用canvas來實現圖表和動畫效果,並給出具體的程式碼範例。二、canvas
 如何用Python繪製動畫圖表
Sep 27, 2023 am 09:53 AM
如何用Python繪製動畫圖表
Sep 27, 2023 am 09:53 AM
如何用Python繪製動畫圖表Python作為一種功能強大的程式語言,可以用於各種資料視覺化和圖表繪製。其中,繪製動畫圖表可以讓數據更加生動有趣。本文將介紹如何使用Python繪製動畫圖表,並提供具體的程式碼範例。首先,我們需要安裝matplotlib函式庫,這是Python中最常用的圖表繪製庫之一。在終端機中執行以下命令安裝matplotlib:pipinsta






