如何使用css實現任意大小及任意方向和任意角度的箭頭
這篇文章主要介紹了使用css實現任意大小、任意方向和任意角度的箭頭示例的相關資料,小編覺得挺不錯的,現在分享給大家,也給大家做個參考。一起跟著小編過來看看吧
網頁開發中,常常會使用到下拉箭頭

,右邊箭頭

{
display: inline-block;
margin: 72px;
border-top: 24px solid;
border-right: 24px solid;
width: 120px;
height: 120px;
transform: rotate(45deg);
}因為這是利用p的border-top, border-right,然後透過旋轉p來實現的。
任意角度的箭頭
transform: matrix(a,b,c,d,e,f)
這個變換矩陣。這裡的6個變數組成了一個3介的變換矩陣任意點p(x,y)的平移, 旋轉, 伸縮變換以及他們的各種組合都可以透過這個變換矩陣做到:註:這裡用齊次座標來表示一個點。簡單說就是p(x, y) 表示為p'(x', y', 1)平移矩陣x' = x txv(x, y) 沿著x軸平移tx, 沿著y軸平移ty。則有:
y' = y ty
所以平移矩陣:
旋轉矩陣
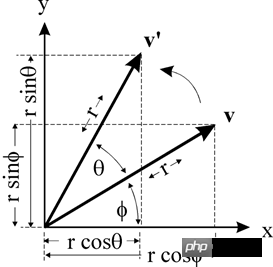 v(x, y) 點繞原點旋轉θ到v'(x', y')
v(x, y) 點繞原點旋轉θ到v'(x', y')
##則有:y' = r * sin(θ ϕ) = r * sin(θ) * cos(ϕ) r * cos(θ) * sin(ϕ ) // 正弦公式x = r * cos(ϕ )
y = r * sin(ϕ )
x' = r * cos(θ ϕ) = r * cos(θ) * cos (ϕ) - r * sin(θ) * sin(ϕ ) // 餘弦公式
所以:y' = x * sin(θ) y * cos(θ)x' = x * cos(θ) - y * sin(θ)
所以旋轉矩陣:
伸縮矩陣##假設x軸, y軸的伸縮率分別是kx, ky。則有:所以:y' = y * ky
x' = x * kx
複合變換
如果是對p(x, y)先平移(變換矩陣A), 然後旋轉(變換矩陣B), 然後伸縮(變換矩陣C)呢?##p' =C(B(Ap)) ==> p' = (CBA)p //矩陣乘法結合率
現在任意角度o的箭頭就很簡單了:
#先把p旋轉45度成為菱形, 變換為M1 伸縮x軸,y軸:
x' = size * cos(o/2) = x * √2 * cos(o/2) y' = size * sin(o/2) = y * √2 * sin(o/2)
即: kx = √2 * cos (o/2); ky = √2 * sin(o/2) 這樣就得到了任意角度的箭頭。變換為 M2
如果箭頭的方向不是指向右側, 在進行一次旋轉就可以得到任意方向的箭頭。變換為M3
那麼由於p' =C(B(Ap)) ==> p' = (CBA)p , 我們就可以先計算出M3 M2 M1,然後對p進行對應的變換,就可以得到任意角度, 任意方向的箭頭了。
p的width和height就是箭頭的邊長, 透過調整可以取得任意邊長的箭頭。
React元件
為了方便使用, 這個箭頭被封裝為了一個 React元件。
範例
簡單箭頭

#模擬select

select

| #props | |||
|---|---|---|---|
| #name | type | default | description |
| degree | number | 90 | |
| #offsetDegree | number | #0 | |
| color | #string | - |
安装使用
npm install rc-arrow --save
import Arrow from 'rc-arrow'
class Hw extends Component {
render() {
return (
<Arrow size="20px" color="red"/>
)
}
}以上就是本文的全部内容,希望对大家的学习有所帮助,更多相关内容请关注PHP中文网!
相关推荐:
以上是如何使用css實現任意大小及任意方向和任意角度的箭頭的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 vue中怎麼用bootstrap
Apr 07, 2025 pm 11:33 PM
vue中怎麼用bootstrap
Apr 07, 2025 pm 11:33 PM
在 Vue.js 中使用 Bootstrap 分為五個步驟:安裝 Bootstrap。在 main.js 中導入 Bootstrap。直接在模板中使用 Bootstrap 組件。可選:自定義樣式。可選:使用插件。
 HTML,CSS和JavaScript的角色:核心職責
Apr 08, 2025 pm 07:05 PM
HTML,CSS和JavaScript的角色:核心職責
Apr 08, 2025 pm 07:05 PM
HTML定義網頁結構,CSS負責樣式和佈局,JavaScript賦予動態交互。三者在網頁開發中各司其職,共同構建豐富多彩的網站。
 了解HTML,CSS和JavaScript:初學者指南
Apr 12, 2025 am 12:02 AM
了解HTML,CSS和JavaScript:初學者指南
Apr 12, 2025 am 12:02 AM
WebDevelovermentReliesonHtml,CSS和JavaScript:1)HTMLStructuresContent,2)CSSStyleSIT和3)JavaScriptAddSstractivity,形成thebasisofmodernWebemodernWebExexperiences。
 bootstrap怎麼寫分割線
Apr 07, 2025 pm 03:12 PM
bootstrap怎麼寫分割線
Apr 07, 2025 pm 03:12 PM
創建 Bootstrap 分割線有兩種方法:使用 標籤,可創建水平分割線。使用 CSS border 屬性,可創建自定義樣式的分割線。
 bootstrap怎麼設置框架
Apr 07, 2025 pm 03:27 PM
bootstrap怎麼設置框架
Apr 07, 2025 pm 03:27 PM
要設置 Bootstrap 框架,需要按照以下步驟:1. 通過 CDN 引用 Bootstrap 文件;2. 下載文件並將其託管在自己的服務器上;3. 在 HTML 中包含 Bootstrap 文件;4. 根據需要編譯 Sass/Less;5. 導入定製文件(可選)。設置完成後,即可使用 Bootstrap 的網格系統、組件和样式創建響應式網站和應用程序。
 bootstrap怎麼插入圖片
Apr 07, 2025 pm 03:30 PM
bootstrap怎麼插入圖片
Apr 07, 2025 pm 03:30 PM
在 Bootstrap 中插入圖片有以下幾種方法:直接插入圖片,使用 HTML 的 img 標籤。使用 Bootstrap 圖像組件,可以提供響應式圖片和更多樣式。設置圖片大小,使用 img-fluid 類可以使圖片自適應。設置邊框,使用 img-bordered 類。設置圓角,使用 img-rounded 類。設置陰影,使用 shadow 類。調整圖片大小和位置,使用 CSS 樣式。使用背景圖片,使用 background-image CSS 屬性。
 bootstrap按鈕怎麼用
Apr 07, 2025 pm 03:09 PM
bootstrap按鈕怎麼用
Apr 07, 2025 pm 03:09 PM
如何使用 Bootstrap 按鈕?引入 Bootstrap CSS創建按鈕元素並添加 Bootstrap 按鈕類添加按鈕文本
 bootstrap怎麼調整大小
Apr 07, 2025 pm 03:18 PM
bootstrap怎麼調整大小
Apr 07, 2025 pm 03:18 PM
要調整 Bootstrap 中元素大小,可以使用尺寸類,具體包括:調整寬度:.col-、.w-、.mw-調整高度:.h-、.min-h-、.max-h-






