動態規劃(dynamic programming)是運籌學的一個分支，是求解決策過程(decision process)最優化的數學方法。
動態規劃演算法通常是基於一個遞推公式及一個或多個初始狀態。目前子問題的解將由上一次子問題的解推出。
要解決一個給定的問題，我們需要解決其不同部分（即解決子問題），再合併子問題的解以得出原問題的解。
通常許多子問題非常相似，為此動態規劃法試圖只解決每個子問題一次，從而減少計算量。
一旦某個給定子問題的解已經算出，則將其記憶化儲存，以便下次需要同一個子問題解之時直接查表。
這種做法在重複子問題的數目關於輸入的規模呈指數增長時特別有用。
動態規劃有三個核心元素：
1.最優子結構
2.邊界
3.狀態轉移方程式
我們來看一到題目
有一座高度是10階的樓梯，從下往上走，每跨一步只能往上1級或2級階梯。求一共有多少種走法。
例如，每次走1級台階，總共走10步，這是其中一種走法。
再比如，每次走2級台階，總共走5步，這是另一種走法。
但是這樣一個個算太麻煩了，我們可以只去思考最後一步怎麼走，如下圖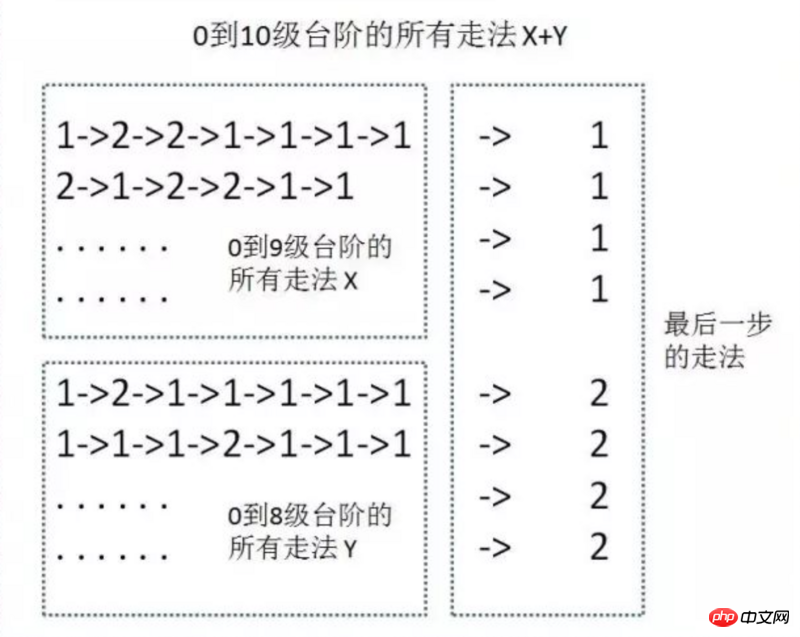
這樣走到第十個樓梯的走法=走到第八個樓梯走到第九個樓梯
我們用f(n)來表示走到第n個樓梯的走法，所以就有了f(10) = f(9) f(8)
然後f(9) = f(8) f(7), f(8) = f(7) f(6)......
這樣我們就得到一個遞歸式：
f(n) = f(n-1) f(n-2);
還有兩個初始狀態 ：
f(1) = 1;
f(2) = 2;
這樣就得到了第一種解法
function getWays(n) { if (n < 1) return 0; if (n == 1) return 1; if (n == 2) return 2; return getWays(n-1) + getWays(n-2); }登入後複製
這種方法的時間複雜度為O(2^n)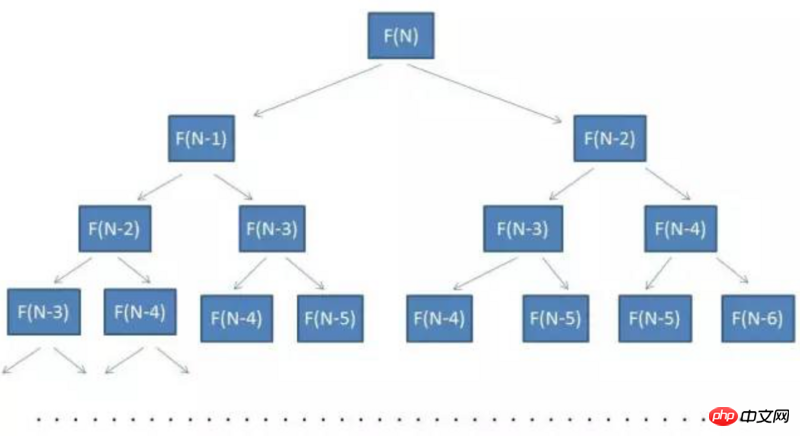
可以看到這是一顆二元樹，數的節點個數就是我們遞歸方程式需要計算的次數，
數的高度為N，節點個數近似於2^n
所以時間複雜度近似於O(2^n)
但是這種方法能不能優化呢？
我們會發現有些值被重複計算，如下圖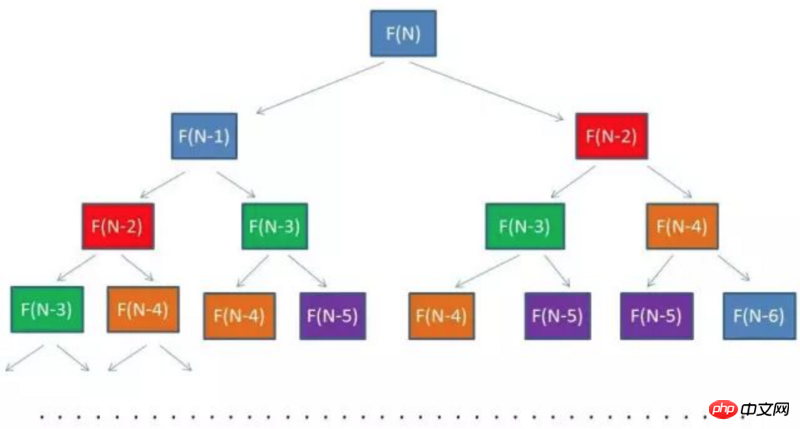
相同顏色代表重複的部分，那麼我們可不可以把這些重複計算的值記錄下來呢？
這樣的最佳化就有了第二種方法
const map = new Map(); function getWays(n) { if (n < 1) return 0; if (n == 1) return 1; if (n == 2) return 2; if (map.has(n)) { return map.get(n); } const value = getWays(n-1) + getWays(n-2); map.set(n, value); return value; }登入後複製
因為map裡最終會存放n-2個鍵值對，所以空間複雜度為O(n),時間複雜度也為O(n)
##繼續想一想這就是最優的解決方案了嗎？ 我們回到一開始的思路，我們是假定前面的樓梯已經走完，只考慮最後一步，所以才得出來f(n) = f(n-1) f(n-2)的遞歸式，這是一個置頂向下求解的式子一般來說，按照正常的思路應該是一步一步往上走，應該是自底向上去求解才比較符合正常人的思維，我們來看看行不行的通
這是一開始走的一個和兩個樓梯的走法數,即之前說的
初始狀態
這是進行了一次迭代得出了3個樓梯的走法，f(3)只依賴f(1) 和f(2)
#這裡又進行了一次迭代得出了4個樓梯的走法，f(4)只依賴f(2) 和f(3)
function getWays(n) {
if (n < 1) return 0;
if (n == 1) return 1;
if (n == 2) return 2;
// a保存倒数第二个子状态数据，b保存倒数第一个子状态数据， temp 保存当前状态的数据
let a = 1, b = 2;
let temp = a + b;
for (let i = 3; i <= n; i++) {
temp = a + b;
a = b;
b = temp;
}
return temp;
}目前時間複雜度仍為
O(n)，但空間複雜度降為O(1)這就是理想的結果
當變化維度變成兩個、三個甚至更多時，會更加複雜，背包問題就是比較典型的多維度問題，有興趣的可以上網看看《背包九講》
相關推薦：
#以上是案例詳解：動態規劃入門（以爬樓梯為例）的詳細內容。更多資訊請關注PHP中文網其他相關文章！
