這篇文章帶給大家的內容是關於帶你簡單了解python創建神經網路模型的內容,有一定的參考價值,有需要的朋友可以參考一下,希望對你有所幫助。
摘要: 對神經網路的工作原理感到好奇?動手實踐一下吧,了解神經網路是如何運作的最佳方法是自己創建一個簡單神經網路。
神經網路(NN),又稱為人工神經網路(ANN),是機器學習領域中學習演算法的子集,大體上借鑒了生物神經網路的概念。目前,神經網路在電腦視覺、自然語言處理等領域應用廣泛。德國資深機器學習專家Andrey Bulezyuk說到,「神經網路正在徹底改變機器學習,因為它們能夠有效地模擬各種學科和行業的複雜抽象,且無需太多人工參與。」
大體上,人工神經網路基本上包含以下元件:
接收資料並傳遞資料的輸入層(input layer);
隱藏層(hidden layer);
輸出層(output layer);
層與層之間的權重(weight);
每個隱藏層使用的激活函數(activation function);
#在本文教程中,使用的是簡單的Sigmoid激活函數,但注意一點,在深層神經網路模型中, sigmoid活化函數一般不作為首選,原因是其易發生梯度擴散現象。
此外,人工神經網路有幾種不同類型的神經網絡,例如前饋神經網路、卷積神經網路及遞歸神經網路等。本文將以簡單的前饋或感知神經網路為例,這種類型的人工神經網路是直接從前到後傳遞資料的,簡稱前向傳播過程。
而訓練前饋神經元通常需要反向傳播演算法,這就需要為網路提供對應的輸入和輸出集。當輸入資料傳輸到神經元時,它會經過相應的處理,並將產生的輸出傳輸給下一層。
下圖簡單展示了一個神經網路結構:
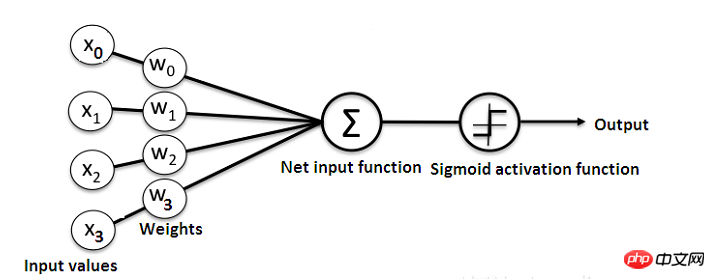
#此外,理解神經網路如何運作的最佳方法是學習如何在不使用任何工具箱的前提下從頭開始建立一個。在本文中,我們將示範如何使用Python創建一個簡單的神經網路。
下表顯示了我們將解決的問題:
我們將訓練神經網絡,以便在提供一組新資料時可以預測正確的輸出值。
從表中看到,輸出的值總是等於輸入節中的第一個值。因此,我們可以期望新情形的輸出(?)值為1。
下面讓我們看看是否可以使用一些Python程式碼來得到相同的結果。
我們將在Python中建立一個NeuralNetwork類別來訓練神經元以提供準確的預測,該類別還包含其他輔助函數。我們不會將神經網路庫用於創建這個簡單的神經網路範例中,但會導入基本的Numpy庫來協助計算。
Numpy函式庫是處理資料的一種基本函式庫,它有以下四種重要的計算方法:
EXP-用於產生所述自然指數;
array-用於產生矩陣;
#dot-用於矩陣相乘;
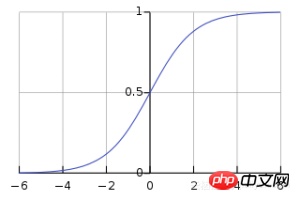
我們將使用Sigmoid函數,它繪製出一個「S」形曲線,將其作為本文創建的神經網路的激活函數。
##################此函數可以將任何值對應到0到1之間,並能幫助我們標準化輸入的加權和。 ######此後,我們將建立Sigmoid函數的導數,以幫助計算權重的基本調整。 ######可以使用Sigmoid函數的輸出來產生其導數。例如,如果輸出變數是“x”,那麼它的導數將是x *(1-x)。 ######訓練模型######訓練模型意味著我們將教導神經網路進行準確預測的階段。每個輸入都有一個權重(weights)-正或負的,這意味著具有大值正權重或大值負權重的輸入將多所得到的輸出有更大地影響。 ######注意,模型訓練最初時,每個權重的初始化都是隨機數。 ###以下是本文建構的神經網路範例問題中訓練過程:############1.從訓練資料集中獲取輸入,根據它們的權重進行一些調整,並透過計算神經網絡輸出的方法來一層一層的傳輸;###2.計算反向傳播的錯誤率。在這種情況下,它是神經元預測得到的輸出與訓練資料集的預期輸出之間的誤差;
3.根據所得的誤差範圍,使用誤差加權導數公式進行一些小的權重調整;
4.將此過程重複15,000次,在每次迭代過程中,同時處理整個訓練集;
在這裡,我們使用「.T」函數對矩陣求偏壓。因此,數字將以這種方式儲存:

最終,神經元的權重將針對所提供的訓練資料進行最佳化。因此,如果神經網路的輸出與期望的輸出一致時,表示訓練完成,可以進行準確的預測,這就是反向傳播的方式。
最後,初始化NeuralNetwork類別後並執行整個程序,以下是如何在Python專案中建立神經網路的完整程式碼:
import numpy as np
class NeuralNetwork():
def __init__(self):
# 设置随机数种子
np.random.seed(1)
# 将权重转化为一个3x1的矩阵,其值分布为-1~1,并且均值为0
self.synaptic_weights = 2 * np.random.random((3, 1)) - 1
def sigmoid(self, x):
# 应用sigmoid激活函数
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(self, x):
#计算Sigmoid函数的偏导数
return x * (1 - x)
def train(self, training_inputs, training_outputs, training_iterations):
# 训练模型
for iteration in range(training_iterations):
# 得到输出
output = self.think(training_inputs)
# 计算误差
error = training_outputs - output
# 微调权重
adjustments = np.dot(training_inputs.T, error * self.sigmoid_derivative(output))
self.synaptic_weights += adjustments
def think(self, inputs):
# 输入通过网络得到输出
# 转化为浮点型数据类型
inputs = inputs.astype(float)
output = self.sigmoid(np.dot(inputs, self.synaptic_weights))
return output
if __name__ == "__main__":
# 初始化神经类
neural_network = NeuralNetwork()
print("Beginning Randomly Generated Weights: ")
print(neural_network.synaptic_weights)
#训练数据
training_inputs = np.array([[0,0,1],
[1,1,1],
[1,0,1],
[0,1,1]])
training_outputs = np.array([[0,1,1,0]]).T
# 开始训练
neural_network.train(training_inputs, training_outputs, 15000)
print("Ending Weights After Training: ")
print(neural_network.synaptic_weights)
user_input_one = str(input("User Input One: "))
user_input_two = str(input("User Input Two: "))
user_input_three = str(input("User Input Three: "))
print("Considering New Situation: ", user_input_one, user_input_two, user_input_three)
print("New Output data: ")
print(neural_network.think(np.array([user_input_one, user_input_two, user_input_three])))
print("Wow, we did it!")以下是執行程式碼後產生的輸出:

以上是我們設法創建的一個簡單的神經網路。首先神經網路開始為自己分配一些隨機權,此後,它使用訓練範例訓練自身。
因此,如果出現新的樣本輸入[1,0,0],則其輸出值為0.9999584。而期望的正確答案是1,可以說二者是非常接近了,考慮到Sigmoid函數是非線性函數,這點誤差是可以接受的。
此外,本文只使用了一層神經網路來執行簡單的任務。如果我們將數千個這些人工神經網路集合在一起會發生什麼情況呢?我們可以100%模仿人類思維嗎?答案是肯定的,但是目前實現起來是比較困難的,只能說是十分相近。對此有興趣的讀者可以閱讀與深度學習相關的資料。
以上是帶你簡單了解python創建神經網路模型的內容的詳細內容。更多資訊請關注PHP中文網其他相關文章!


