這篇文章帶給大家的內容是關於JavaScript二元樹（二元搜尋樹）的詳細介紹，有一定的參考價值，有需要的朋友可以參考一下，希望對你有幫助。
可能有一部分人沒有讀過我上一篇寫的二元堆，所以這裡把二元樹的基本概念複製過來了，如果讀過的人可以忽略前面針對二元樹基本概念的介紹，另外如果對鍊錶資料結構不清楚的最好先看一下本人之前寫的js資料結構-鍊錶
二叉樹(Binary Tree)是一種樹狀結構，它的特徵是每個節點最多只有兩個分支節點，一棵二元樹通常由根節點，分支節點，葉子節點組成。而每個分支節點也常被稱為一棵子樹。
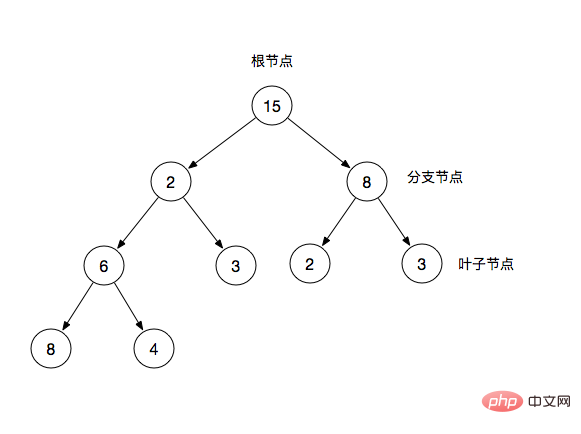
根節點：二元樹最頂層的節點
在二元樹中，我們常常也會用父節點和子節點來描述，比如圖中2為6和3的父節點，反之6和3是2子節點
二叉樹的三個性質
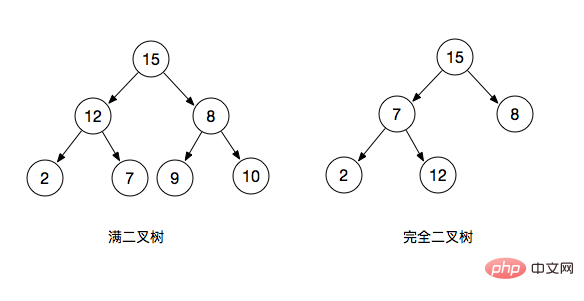二元搜尋樹
一組資料：12,4,18,1,8,16,20
由下圖可以看出，左邊的圖滿足了二元樹的性質，它的每個左子節點都小於父節點，右子節點大於其父節點，同時左子樹的節點都小於根節點，右子樹的節點都大於根節點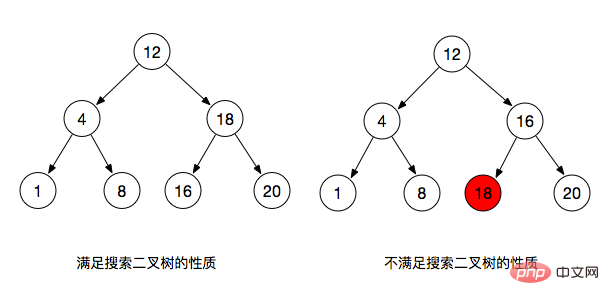
# #二元搜尋樹主要的幾個操作：
##遍歷（transverse）
class BinaryTreeNode {
constructor(key, value){
this.parent = null;
this.left = null;
this.right = null;
this.key = key;
this.value = value;
}
}在二叉搜索树中我们会维护一个root指针，这个就相当于链表中的head指针，在没有任何节点插入的时候它指向空，在有节点插入以后它指向根节点。
class BinarySearchTree {
constructor() {
this.root = null;
}
} static createNode(key, value) {
return new BinarySearchTree(key, value);
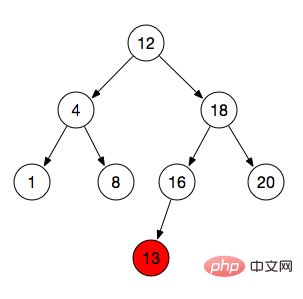
}看下面这张图，13是我们要插入的节点，它插入的具体步骤：
跟根节点12做比较，比12大，所以我们确定了，这个节点是往右子树插入的
而根节点的右边已经有节点，那么跟这个节点18做比较，结果小于18所以往18的左节点找位置
而18的左节点也已经有节点了，所以继续跟这个节点做比较，结果小于16
刚好16的左节点是空的(left=null)，所以13这个节点就插入到了16的左节点
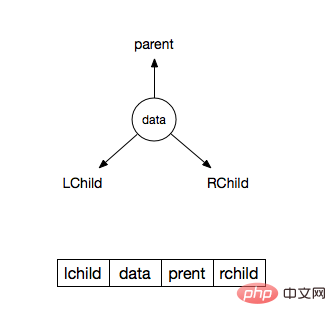
通过上面的描述，我们来看看代码是怎么写的
定义两个指针，分别是p和tail，最初都指向root，p是用来指向要插入的位置的父节点的指针，而tail是用来查找插入位置的，所以最后它会指向null，用上图举个例子，p最后指向了6这个节点，而tail最后指向了null（tail为null则说明已经找到了要插入的位置）
循环，tail根据我们上面分析的一步一步往下找位置插入，如果比当前节点小就往左找，大则往右找，一直到tail找到一个空位置也就是null
如果当前的root为null，则说明当前结构中并没有节点，所以插入的第一个节点直接为跟节点，即this.root = node
将插入后的节点的parent指针指向父节点
insert(node){
let p = this.root;
let tail = this.root;
// 循环遍历，去找到对应的位置
while(tail) {
p = tail;
// 要插入的节点key比当前节点小
if (node.key <h3>查找</h3><p>查找就很简单了，其实和插入差多，都是去别叫左右节点的大小，然后往下找</p>如果root = null, 则二叉树中没有任何节点，直接return，或者报个错什么的。
循环查找
search(key) {
let p = this.root;
if(!p) {
return;
}
while(p && p.key !== key){
if(p.key<key><h3>遍历</h3>
<ul class=" list-paddingleft-2">
<li><p>中序遍历(inorder)：先遍历左节点，再遍历自己，最后遍历右节点，输出的刚好是有序的列表</p></li>
<li><p>前序遍历(preorder)：先自己，再遍历左节点，最后遍历右节点</p></li>
<li><p>后序遍历(postorder)：先左节点，再右节点，最后自己</p></li>
</ul>
<p>最常用的一般是中序遍历，因为中序遍历可以得到一个已经排好序的列表，这也是为什么会用二叉搜索树排序的原因</p>
<p>根据上面对中序遍历的解释，那么代码就变的很简单，就是一个递归的过程，递归停止的条件就是节点为null</p>
<ul class=" list-paddingleft-2">
<li><p>先遍历左节点-->yield* this._transverse(node.left)</p></li>
<li><p>遍历自己 --> yield* node</p></li>
<li><p>遍历左节点 --> yield* this._transverse(node.right)</p></li>
</ul>
<pre class="brush:php;toolbar:false"> transverse() {
return this._transverse(this.root);
}
*_transverse(node){
if(!node){
return;
}
yield* this._transverse(node.left);
yield node;
yield* this._transverse(node.right)
}
看上面这张图，我们简化的来看一下，先访问左节点4，再自己12，然后右节点18，这样输出的就刚好是一个12，4，8
补充：这个地方用了generater，所以返回的一个迭代器。可以通过下面这种方式得到一个有序的数组，这里的前提就当是已经有插入的节点了
const tree = new BinaryTree(); //...中间省略插入过程 // 这样就返回了一个有序的数组 var arr = [...tree.transverse()].map(item=>item.key);
class BinaryTreeNode {
constructor(key, value) {
// 指向父节点
this.p = null;
// 左节点
this.left = null;
// 右节点
this.right = null;
// 键
this.key = key;
// 值
this.value = value;
}
}
class BinaryTree {
constructor() {
this.root = null;
}
static createNode(key, value) {
return new BinaryTreeNode(key, value);
}
search(key) {
let p = this.root;
if (!p) {
return;
}
while (p && p.key !== key) {
if (p.key <h3>总结</h3><p>二叉查找树就讲完了哈，其实这个和链表很像的，还是操作那么几个指针，既然叫查找树了，它主要还是用来左一些搜索，还有就是排序了，另外补充一下，二叉查找树里找最大值和最小值也很方便是不是，如果你大致读懂了的话。</p><p class="comments-box-content"></p>以上是JavaScript二元樹（二元搜尋樹）的詳細介紹的詳細內容。更多資訊請關注PHP中文網其他相關文章！
