如何理解資料結構與演算法（Python）

Python中資料結構和演算法的理解：Python中資料結構指的是靜態的描述資料元素之間的關係，演算法指的是解決問題的方法或步驟，換句話說演算法是為了解決實際問題而設計的，資料結構是演算法需要處理的問題載體。

資料結構和演算法是程式開發人員的必備基本功，所以需要我們平時不斷的主動去學習積累，接下來將自在文章中為大家具體介紹這兩個知識點，希望對大家有幫助。

【推薦課程：Python教學】

引入概念

先來看一題:

若a b c=1000，且a2 b2=c^2（a,b,c 為自然數），如何求出所有a、b、c可能的組合?

第一次嘗試

import time
start_time = time.time()
# 注意是三重循环
for a in range(0, 1001):    
for b in range(0, 1001):        
for c in range(0, 1001):            
if a**2 + b**2 == c**2 and a+b+c == 1000:
print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()
print("elapsed: %f" % (end_time - start_time))
print("complete!")

運行結果：

a, b, c: 0, 500, 500
a, b, c: 200, 375, 425
a, b, c: 375, 200, 425
a, b, c: 500, 0, 500
elapsed: 1066.117884
complete!

運行時間竟然多達17.8分鐘

演算法的提出

#演算法的概念

##演算法是電腦處理訊息的本質，因為電腦程式本質上是一個演算法來告訴電腦確切的步驟來執行一個指定的任務。一般地，當演算法在處理資訊時，會從輸入設備或數據的儲存位址讀取數據，把結果寫入輸出設備或某個儲存位址供以後再呼叫。

演算法是獨立存在的一種解決問題的方法和想法。
對於演算法而言，實現的語言並不重要，重要的是思想。
演算法可以有不同的語言描述實作版本（如C描述、C 描述、Python描述等），我們現在是在用Python語言進行描述實作。

演算法的五大特性

輸入: 演算法具有0個或多個輸入

輸出: 演算法至少有1個或多個輸出

有窮性: 演算法在有限的步驟之後會自動結束而不會無限循環，並且每一個步驟可以在可接受的時間內完成

#確定性：演算法中的每一步都有確定的意義，不會出現二義性

可行性：演算法的每一步都是可行的，也就是說每一步都能夠執行有限的次數完成

# #第二次嘗試

import time
start_time = time.time()
# 注意是两重循环
for a in range(0, 1001):    
for b in range(0, 1001-a):
c = 1000 - a - b        
if a**2 + b**2 == c**2:            
print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()print("elapsed: %f" % (end_time - start_time))print("complete!")

運行結果：

a, b, c: 0, 500, 500
a, b, c: 200, 375, 425
a, b, c: 375, 200, 425
a, b, c: 500, 0, 500
elapsed: 0.632128

注意運行時間0.632128秒

演算法效率衡量

##執行時間反應演算法效率

對於同一個問題，我們給了兩種解決演算法，在兩種演算法的實作中，我們對程式執行的時間進行了測算，發現兩段程式執行的時間相差懸殊，由此我們可以得出一個結論：實作演算法程式的執行時間可以反映出演算法的效率，也就是演算法的優劣。

單靠時間值絕對可信嗎？

假設我們將第二次嘗試的演算法程式運行在一台配置古老效能低的電腦中，情況會如何？很可能運行的時間並不會比在我們的電腦中運行演算法一的時間快多少。 #########單純依靠運行的時間來比較演算法的優劣不一定是客觀準確的！ #########程式的運作離不開電腦環境（包括硬體和作業系統），這些客觀原因會影響程式運作的速度並反應在程式的執行時間上。那麼如何才能客觀的評判一個演算法的優劣呢？ #########時間複雜度與「大O記法」#########我們假定電腦執行演算法每一個基本運算的時間是固定的一個時間單位，那麼有多少個基本操作就代表會花費多少時間單位。既然對於不同的機器環境而言，確切的單位時間是不同的，但是對於演算法進行多少個基本操作(即花費多少時間單位)在規模數量級上卻是相同的，因此可以忽略機器環境的影響而客觀的反應演算法的時間效率。 ######對於演算法的時間效率，我們可以用「大O記法」來表示。 ######「大O記法」：對於單調的整數函數f，如果存在一個整數函數g和實常數c>0，使得對於充分大的n總有f(n)<=c* g(n)，就說函數g是f的一個漸近函數（忽略常數），記為f(n)=O(g(n))。也就是說，在趨向無窮的極限意義下，函數f的成長速度受到函數g的約束，也就是函數f與函數g的特徵相似。 ######時間複雜度：假設存在函數g，使得演算法A處理規模為n的問題範例所用時間為T(n)=O(g(n))，則稱O(g(n))為演算法A的漸近時間複雜度，簡稱時間複雜度，記為T(n)##########如何理解「大O記法」######

对于算法进行特别具体的细致分析虽然很好，但在实践中的实际价值有限。对于算法的时间性质和空间性质，最重要的是其数量级和趋势，这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。例如，可以认为3n2和100n2属于同一个量级，如果两个算法处理同样规模实例的代价分别为这两个函数，就认为它们的效率“差不多”，都为n2级。

最坏时间复杂度

分析算法时，存在几种可能的考虑：

算法完成工作最少需要多少基本操作，即最优时间复杂度

算法完成工作最多需要多少基本操作，即最坏时间复杂度

算法完成工作平均需要多少基本操作，即平均时间复杂度
对于最优时间复杂度，其价值不大，因为它没有提供什么有用信息，其反映的只是最乐观最理想的情况，没有参考价值。

对于最坏时间复杂度，提供了一种保证，表明算法在此种程度的基本操作中一定能完成工作。

对于平均时间复杂度，是对算法的一个全面评价，因此它完整全面的反映了这个算法的性质。但另一方面，这种衡量并没有保证，不是每个计算都能在这个基本操作内完成。而且，对于平均情况的计算，也会因为应用算法的实例分布可能并不均匀而难以计算。

因此，我们主要关注算法的最坏情况，亦即最坏时间复杂度。

时间复杂度的几条基本计算规则

基本操作，即只有常数项，认为其时间复杂度为O(1)

顺序结构，时间复杂度按加法进行计算

循环结构，时间复杂度按乘法进行计算

分支结构，时间复杂度取最大值

判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略

在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度

算法分析

第一次尝试的算法核心部分

or a in range(0, 1001):    
for b in range(0, 1001):        
for c in range(0, 1001):            
if a**2 + b**2 == c**2 and a+b+c == 1000:
print("a, b, c: %d, %d, %d" % (a, b, c))

时间复杂度：

T(n) = O(n * n * n) = O(n³)

第二次尝试的算法核心部分

for a in range(0, 1001):    
for b in range(0, 1001-a):
c = 1000 - a - b        
if a**2 + b**2 == c**2:            
print("a, b, c: %d, %d, %d" % (a, b, c))

时间复杂度：

T(n) = O(n * n * (1+1)) = O(n * n) = O(n²)

由此可见，我们尝试的第二种算法要比第一种算法的时间复杂度好多的。

常见时间复杂度

执行次数函数举例	阶	非正式术语
12	O(1)	常数阶
2n + 3	O(n)	线性阶
3n² +2n + 1	O(n²)	平方阶
5log2n+20	O(logn)	对数阶
2n+3nlog2n+19	O(nlogn)	nlogn阶
6n³ +2n² +3n + 1	O(n³)	立方阶
2n	O(2n)	指数阶

注意，经常将log2n（以2为底的对数）简写成logn

常见时间复杂度之间的关系

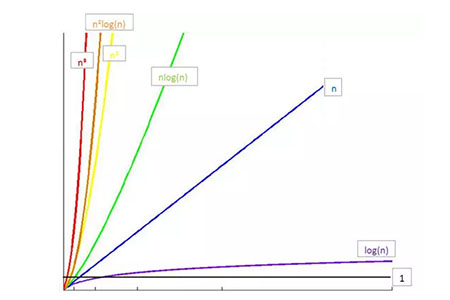
所消耗的时间从小到大

O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)

Python内置类型性能分析

timeit模块

timeit模块可以用来测试一小段Python代码的执行速度。

class timeit.Timer(stmt=&#39;pass&#39;, setup=&#39;pass&#39;, timer=<timer function>)

Timer是测量小段代码执行速度的类。

stmt参数是要测试的代码语句（statment）

setup参数是运行代码时需要的设置

timer参数是一个定时器函数，与平台有关。

timeit.Timer.timeit(number=1000000)

Timer类中测试语句执行速度的对象方法。number参数是测试代码时的测试次数，默认为1000000次。方法返回执行代码的平均耗时，一个float类型的秒数。

list的操作测试

def test1():
   l = []   for i in range(1000):
      l = l + [i]def test2():
   l = []   for i in range(1000):
      l.append(i)def test3():
   l = [i for i in range(1000)]def test4():
   l = list(range(1000))from timeit import Timer
t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "seconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "seconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "seconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "seconds")
# ('concat ', 1.7890608310699463, 'seconds')
# ('append ', 0.13796091079711914, 'seconds')
# ('comprehension ', 0.05671119689941406, 'seconds')
# ('list range ', 0.014147043228149414, 'seconds')

pop操作测试

x = range(2000000)
pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "seconds")
x = range(2000000)
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "seconds")
# ('pop_zero ', 1.9101738929748535, 'seconds')
# ('pop_end ', 0.00023603439331054688, 'seconds')

测试pop操作：从结果可以看出，pop最后一个元素的效率远远高于pop第一个元素

可以自行尝试下list的append(value)和insert(0,value),即一个后面插入和一个前面插入？？？

list内置操作的时间复杂度

dict内置操作的时间复杂度

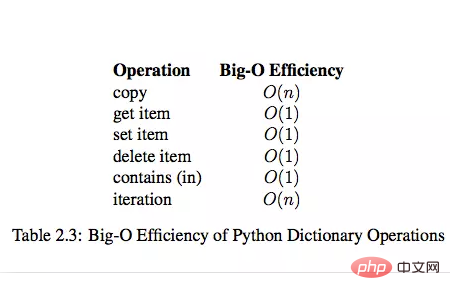
数据结构

概念

数据是一个抽象的概念，将其进行分类后得到程序设计语言中的基本类型。如：int，float，char等。数据元素之间不是独立的，存在特定的关系，这些关系便是结构。数据结构指数据对象中数据元素之间的关系。

Python给我们提供了很多现成的数据结构类型，这些系统自己定义好的，不需要我们自己去定义的数据结构叫做Python的内置数据结构，比如列表、元组、字典。而有些数据组织方式，Python系统里面没有直接定义，需要我们自己去定义实现这些数据的组织方式，这些数据组织方式称之为Python的扩展数据结构，比如栈，队列等。

算法与数据结构的区别

数据结构只是静态的描述了数据元素之间的关系。

高效的程序需要在数据结构的基础上设计和选择算法。

程序 = 数据结构 + 算法

总结：算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体

抽象数据类型(Abstract Data Type)

抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起，进行封装。引入抽象数据类型的目的是把数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开，使它们相互独立。

最常用的数据运算有五种

插入

删除

修改

查找

排序

以上是如何理解資料結構與演算法（Python）的詳細內容。更多資訊請關注PHP中文網其他相關文章！