二分查找演算法

二分查找也稱為折半查找（Binary Search），它是一種效率較高的查找方法。但是，折半查找要求線性表必須採用順序儲存結構，且表格中元素依關鍵字有序排列。

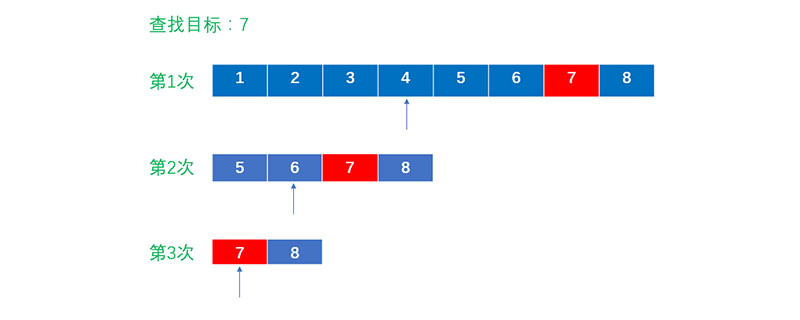
尋找過程

#首先，假設表中元素是按升序排列，將表中間位置記錄的關鍵字與查找關鍵字比較，如果兩者相等，則查找成功；否則利用中間位置記錄將表分成前、後兩個子表，如果中間位置記錄的關鍵字大於查找關鍵字，則進一步查找前一子表，否則進一步查找後一子表。重複以上過程，直到找到符合條件的記錄，使查找成功，或直到子表不存在為止，此時查找不成功。

比較次數

計算公式：

#當順序表有n個關鍵字時：

#查找失敗時，至少比較a次關鍵字；尋找成功時，最多比較關鍵字次數是b。

注意：a,b,n均為正整數。

演算法複雜度

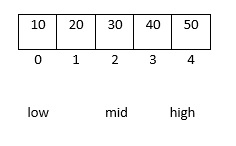
二分查找的基本思想是將n個元素分成大致相等的兩部分，取a[n/2]與x做比較，如果x=a[n/2],則找到x,演算法中止；如果xa[n/2],則只要在陣列a的右半部搜尋x.

時間複雜度無非就是while循環的次數！

總共有n個元素，

漸漸跟下去就是n,n/2,n/4,....n/2^k（接下來運算元素的剩餘個數），其中k就是循環的次數

由於你n/2^k取整後>=1

即令n/2^k=1

可得k=log2n,（是以2為底，n的對數）

所以時間複雜度可以表示O(h)=O(log2n)

下面提供一段二分找出實作的偽代碼:

BinarySearch(max,min,des)

mid-<(max min)/2

while(min<= max)

mid=(min max)/2

if mid=des then

return mid

elseif mid >des then

max=mid-1

else

min=mid 1

#return max

折半查找法也稱為二分查找法，它充分利用了元素間的次序關係，採用分治策略，可在最壞的情況下用O(log n)完成搜尋任務。它的基本想法是：（這裡假設數組元素呈升序排列）將n個元素分成個數大致相同的兩半，取a[n/2]與欲查找的x作比較，如果x=a[n/ 2]則找到x，演算法終止；如果xa[n/2]，則我們只要在數組a的右半部繼續搜尋x。

以上是二分查找演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章！