fipy
菲克定律是指在不依賴宏觀的混合作用發生的傳質現象時,描述分子擴散過程中傳質通量與濃度梯度之間關係的定律。菲克定律是阿道夫·菲克(Adolf Fick)於1855年提出。

由菲克第二定律可以得到動態擴散的偏微分方程。解可以得到濃度分佈和流出曲線。
不確定這個問題有沒有解析解,不過數值解是較通用的解決方法。
fipy是目前難得的還活著的PDE求解python包,作者根據官方範例改寫本程式。
相關推薦:《python影片教學》
#問題
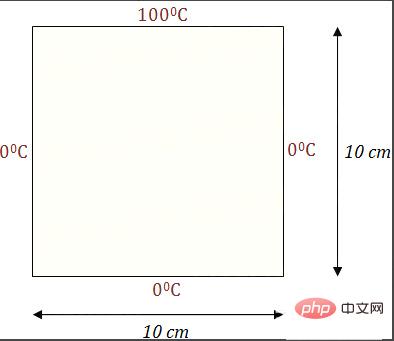
一個二維平板,頂端1攝氏度(100也可以,只是一個係數),另外三個邊緣0攝氏度,初始時刻整個板子都是0攝氏度,隨之時間的推進,熱量在板子上傳遞,最後達到平衡態,我們不僅希望知道平衡態的溫度分佈,也希望知道溫度隨時間是如何變化的。熱量的傳遞由微分方程式給出,可以簡單地理解為熱量按照溫度降低最快的方向傳遞。
公式右邊是溫度的梯度,左邊是溫度隨時間的變化
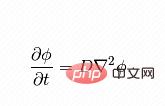
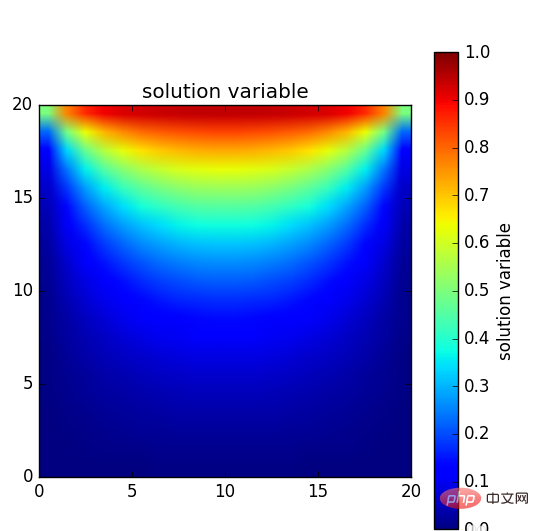
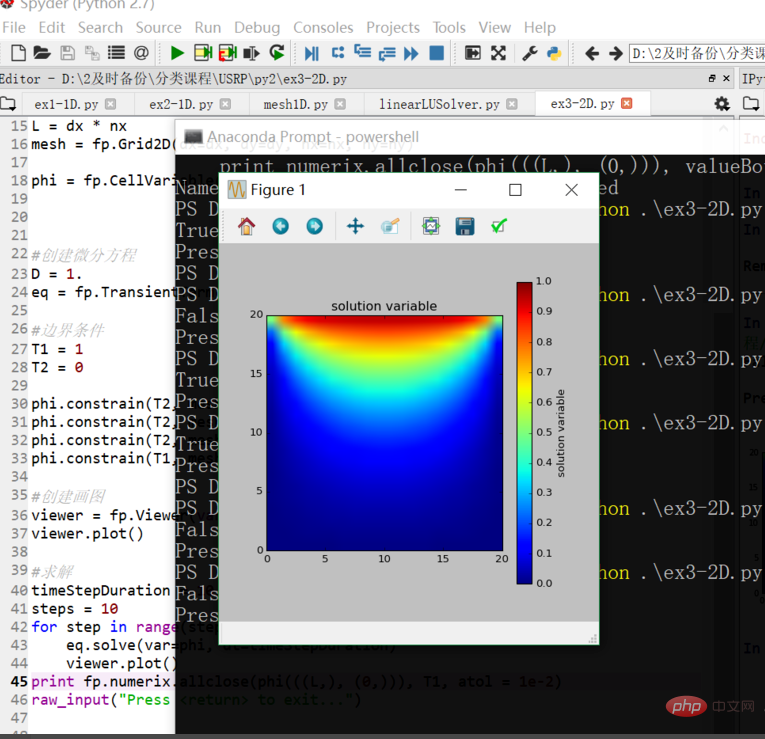
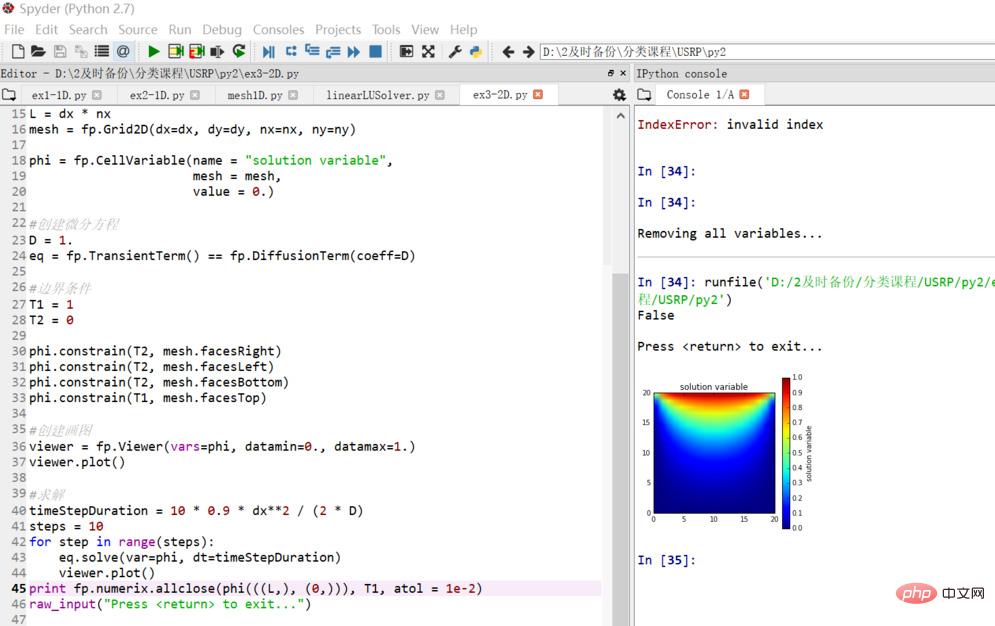
最後整個板子的溫度分佈大致呈現怎樣
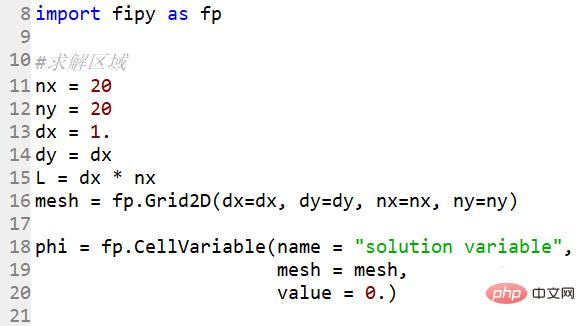
只有一個套件需要導入
import fipy as fp
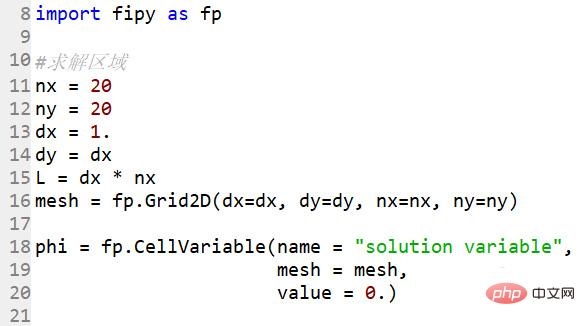
#確定求解區域,一個20*20的格點
#求解區域nx = 20ny = 20dx = 1.dy = dxL = dx * nxmesh = fp.Grid2D(dx=dx, dy=dy, nx=nx, ny=ny)
phi = fp.CellVariable(name = "solution variable",
##建立微分方程
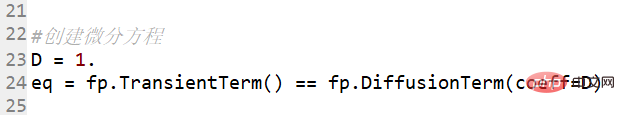
設定邊界條件

#建立畫圖

求解
以上是Python是能解偏微分方程嗎的詳細內容。更多資訊請關注PHP中文網其他相關文章!

